AlphaGo其实很简单~
摘要
由于其巨大的搜索空间以及评估棋盘状态和落子的难度，围棋一直被认为是人工智能经典游戏中最具挑战性的游戏。在这篇文章里，作者介绍了一种新的AI围棋方法，它使用“价值网络”来评估棋盘位置和“策略网络”来选择落子。主模型以深度神经网络为主，训练由对人类专家的经验进行监督学习和自对弈的强化学习组成。研究者将训练成的价值网络、策略网络应用到蒙特卡洛搜索的过程中，从而增加了每个落子的价值。使用这种搜索算法，AlphaGo对其他围棋程序的胜率达到了99.8%，并以5比0击败了人类欧洲围棋冠军。
技术路线
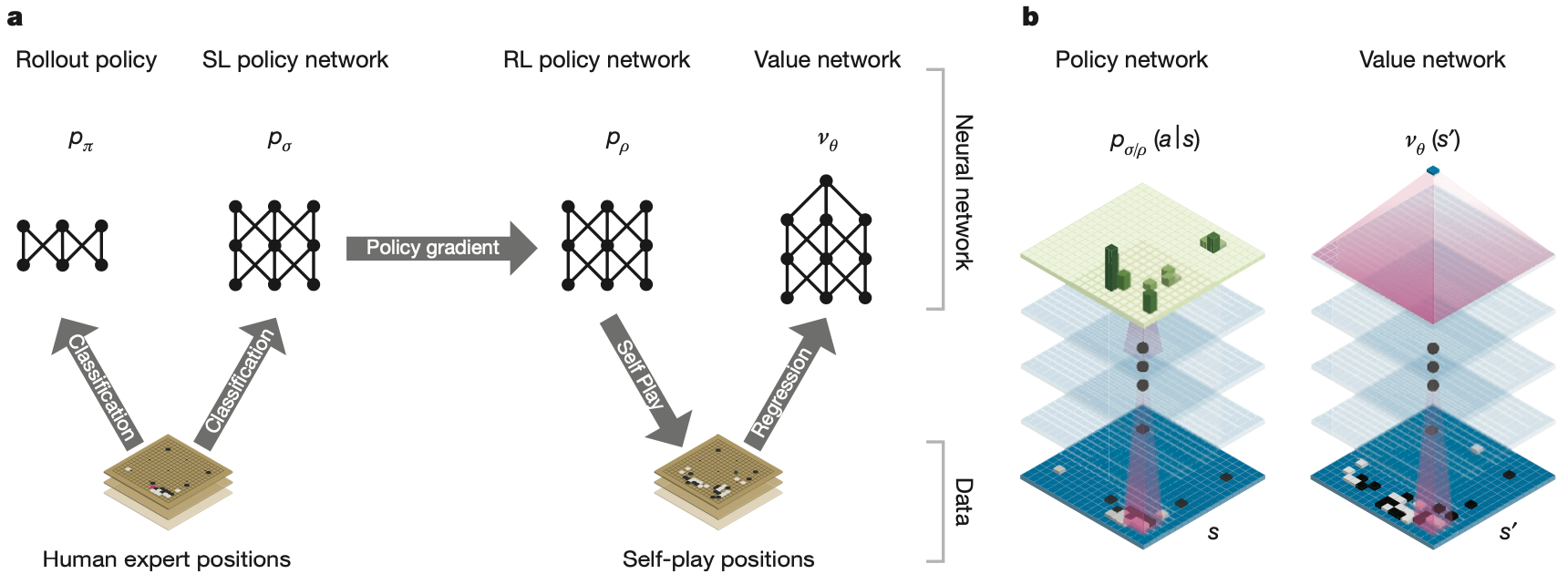
图a：p_{\pi} 和 p_{\sigma} 使用监督学习学习人类专家在不同棋盘状态下的落子，p_{\pi} 是一个更加轻量级的网络。p_{\rho} 的网络架构和 p_{\sigma} 想同，并且参数被初始化为训练好的p_{\sigma} 的参数，然后通过策略梯度强化学习自对弈进行改进，以最大化获胜的概率。通过使用强化学习策略网络 p_{\rho} 自对弈生成一个新的数据集。最后，回归训练一个价值网络 v_{\theta}，以根据新数据集中的数据学习当前棋盘玩家获胜的期望。
图b：AlphaGo 中使用的神经网络架构的示意图。策略网络将棋盘状态 s 作为输入，通过参数为 \sigma 或 \rho的策略网络输出概率分布 p_{\sigma}(a|s) 或 p_{\rho}(a|s) 表示为了取胜当前棋盘每个合法位置的落子收益期望。价值网络类似地使用多个卷积层，参数为 \theta，输出一个标量值 v_{\theta}(s') 来预测当前棋盘状态的获胜期望。
策略网络的监督学习
训练的第一个阶段是使用监督学习学习人类专家的经验。SL 策略网络 p_{\sigma}(a|s) 在权重为 \sigma 的卷积层和非线性整流器之间交替，最终的 softmax 层输出所有合法落子位置的概率分布。策略网络的输入是棋盘状态的简单表示。策略网络在随机采样的状态-动作对上进行训练，使用随机梯度上升来最大化在状态 s 中选择的人类动作的可能性
\Delta\sigma\propto\frac{\partial p_{\sigma}(a|s)}{\partial\sigma} 作者从 KGS Go Server 的 3000 万个状态-动作训练了一个 13 层的策略网络，称为 SL(SupervisedLearning) 策略网络。该网络预测在测试集上的准确率为 57.0%，远远高于基准模型的 44.4%。然而，准确性的小幅提高会导致计算开销的增长，较大的网络可以获得更好的准确性，但在搜索过程中评估速度较慢。作者还训练了一个更快但不太准确的策略网络 p_{\pi}(a|s)，使用更轻量级的特征的线性 softmax 达到了 24.2% 的准确率。p_{\pi}(a|s)选择一个动作只需要2 \mu s，比p_{\sigma}(a|s) 的3 ms要快得多。
策略网络的强化学习
训练的第二阶段旨在通过策略梯度强化学习 (RL) 改进策略网络。RL 策略网络 p_{\rho} 在结构上与 SL 策略网络相同，并且其权重 \rho 被初始化为相同的值，即 \rho = \sigma。使用随机化的动作采样策略放置过拟合，每个episode结束的时候设定胜方的reward为1，负方的reward为-1。然后在每个时间步 t，通过随机梯度上升最大化获胜的期望
\Delta\sigma\propto\frac{\partial p_{\rho}(a_t|s_t)}{\partial\sigma}z_t.值网络的强化学习
训练的最后一个阶段是评估每个棋盘状态获胜的期望，估计一个价值函数 v^p(s)，训练时双方玩家都使用策略 p 预测的位置 s 的结果
v^p(s)=\mathbb{E}[z_t=z|s_t=s,a_{t\cdots T}\sim p]. RL价值网络与策略网络有相似的结构，参数为 \theta，使用策略梯度的MSE进行更新
\Delta\sigma\propto\frac{\partial v_{\theta}(s)}{\partial\theta}(z-v_{\theta}(s)).蒙特卡洛搜索
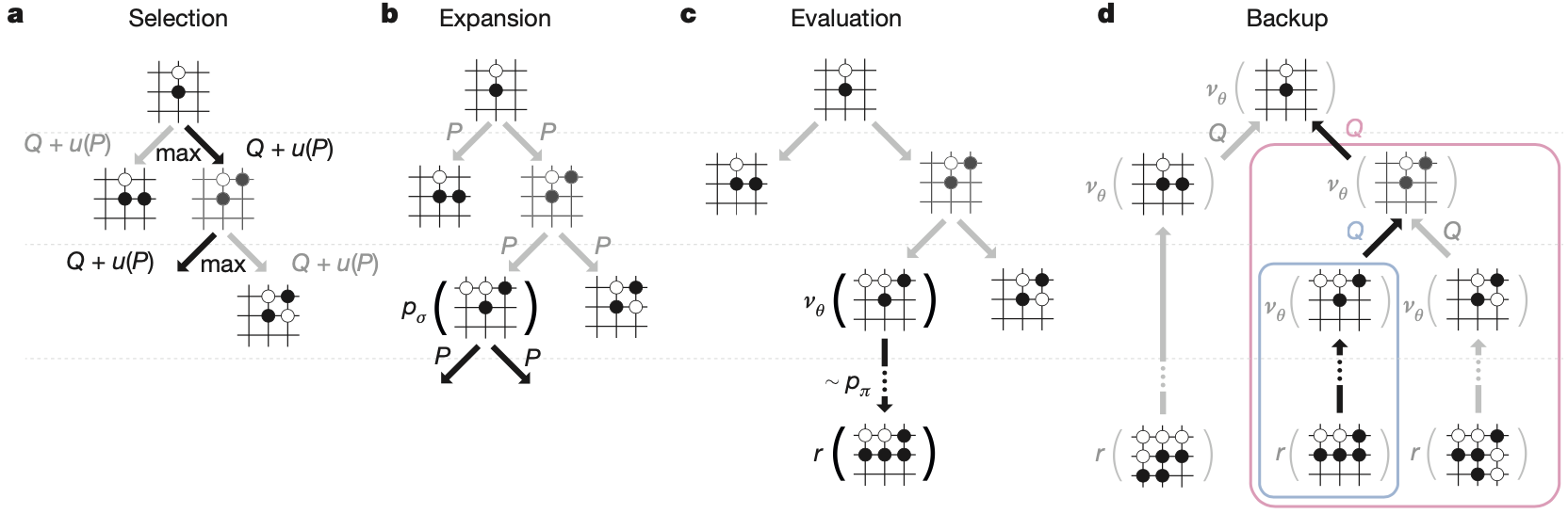
在对战中，AlphaGo 在 MCTS 算法中结合了策略和价值网络，该算法通过前瞻搜索来选择动作。搜索树的每条边 (s, a) 存储一个动作值 Q(s, a)、访问计数 N(s, a) 和先验概率 P(s, a)。从根状态开始模拟遍历可能的棋盘状态。 在每个模拟的每个时间步 t，从状态 s_t 中选择一个动作 a_t
a_t = \arg\max_a(Q(s_t,a)+u(s_t,a))来最大化价值+bonus
u(s,a) \propto \frac{P(s,a)}{1+N(s,a)}. Bonus 正比于先验概率，但是随着访问次数递减。当遍历在第L步到达叶节点 s_L 时，叶节点继续扩展，节点 s_L 仅由 SL 策略网络 p_\sigma 处理一次得到新的叶节点，输出概率存储为每个合法动作 a 的先验概率 P，p(s,a) = p_\sigma(a|s)。叶节点以两种不同的方式进行评估：首先是价值网络 v_\theta(s_L)；其次，通过使用轻量级策略网络 \pi 随机出的从 L 直到最终步骤 T，使用混合参数 \lambda 将这些评估组合成叶节点的评估
V(s_L)=(1-\lambda)v_\theta(s_L)+\lambda z_L.在模拟结束时，更新所有遍历到的边的动作值和访问次数
N(s,a)=\sum_{i=1}^{n}1(s,a,i)\\
Q(s,a)=\frac{1}{N(s,a)}\sum_{i=1}^{n}1(s,a,i)V(s_L^i). 其中 s_i 是第 i 次模拟的叶节点，1(s, a, i) 表示在第 i 次模拟期间是否遍历了边 (s, a)。搜索完成后，算法从根位置选择访问次数最多的移动，因为这是根据概率分布采样的，被访问的次数阅读说明价值越大。