时间差分（Temporal-Difference\ TD）学习是强化学习的一种新颖的方法。TD 学习是蒙特卡洛（MC）思想和动态规划（DP）思想的结合。与蒙特卡罗方法一样，TD 方法可以直接从经验中学习，与 DP 一样，TD 方法部分基于其他状态的值函数估计来更新当前状态的估计， TD、DP 和 Monte Carlo 方法之间的关系将会是强化学习中反复探讨的问题，这三个方法的差异主要来自它们对策略评估的差异。和之前一样，我们首先介绍策略评估，或者叫预测问题，即估计给定策略的值函数；然后介绍控制问题，即寻找最优策略。
策略验证
TD 方法和 Monte Carlo 方法都使用经验来进行策略评估。蒙特卡罗方法等到当前的 episode 结束后，将获得的 return 对值函数进行迭代更新。适用于 nonstationary 问题的 MC 方法如下
V(S_t) = V(S_t) + \alpha[G_t-V(S_t)]. 而 TD 方法的公式在Monte Carlo 方法的基础之上做改进如下
V(S_t) = V(S_t) + \alpha[R_{t+1}+\gamma V(S_{t+1})-V(S_t)],公式中将 G_t 替换为 R_{t+1}，然后又在增量项中增加了 \gamma V(S_{t+1})。
将 G_t 替换为 R_{t+1} 意味着在时间差分方法中，不再是等每个episode结束之后才更新值函数，而是在每次做完 action 获得 reward 之后就进行迭代更新。在增量项中增加的 \gamma V(S_{t+1}) 是从动态规划来的，依据的公式是
v_\pi(s) = \mathbb{E}_\pi[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s].于是，时间差分方法的策略评估的伪代码如下所示
策略优化
关于策略优化，分为两种：on-policy 和 off-policy。
on-policy优化
在on-policy优化中，我们需要更新维护的是动作值函数，而不是状态值函数，通过动作值函数，可以直接基于前面提到的 greedy 方法进行策略优化。
动作值函数的迭代与状态值函数类似，如下
Q(S_t,A_t) = Q(S_t,A_t) + \alpha[R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)].优化的伪代码如下
off-policy优化
off-policy优化说的是控制策略和目标策略不一致的优化方法，这里控制策略依然是采用 \epsilon-greedy 方法，而目标策略则直接是最优策略 \pi_*，动作值函数更新方法为
Q(S_t,A_t) = Q(S_t,A_t) + \alpha[R_{t+1}+\gamma \max_aQ(S_{t+1},a)-Q(S_t,A_t)].优化的伪代码如下
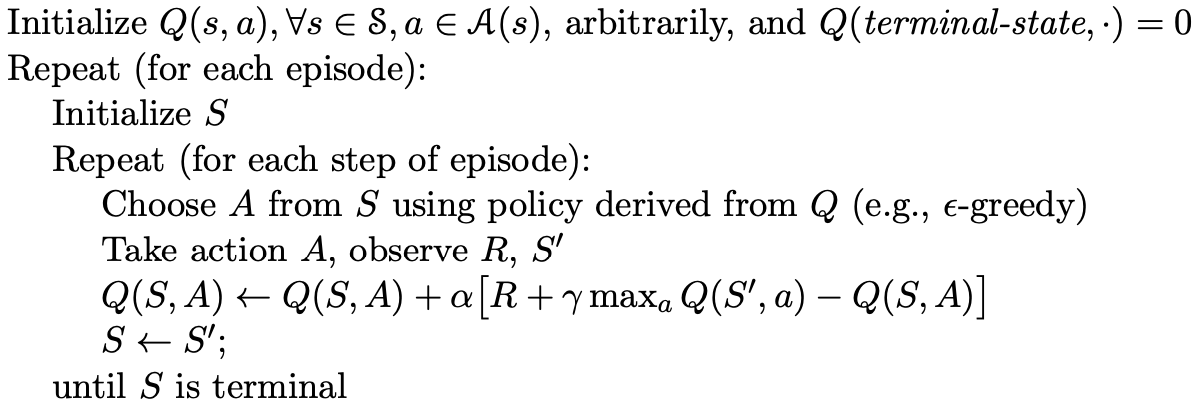
总结
以上就是时间差分方法，基于以前分享过的basic的知识，对于时间差分的学习就很简单了，下次我们分享强化学习中的Eligibility\ Traces。