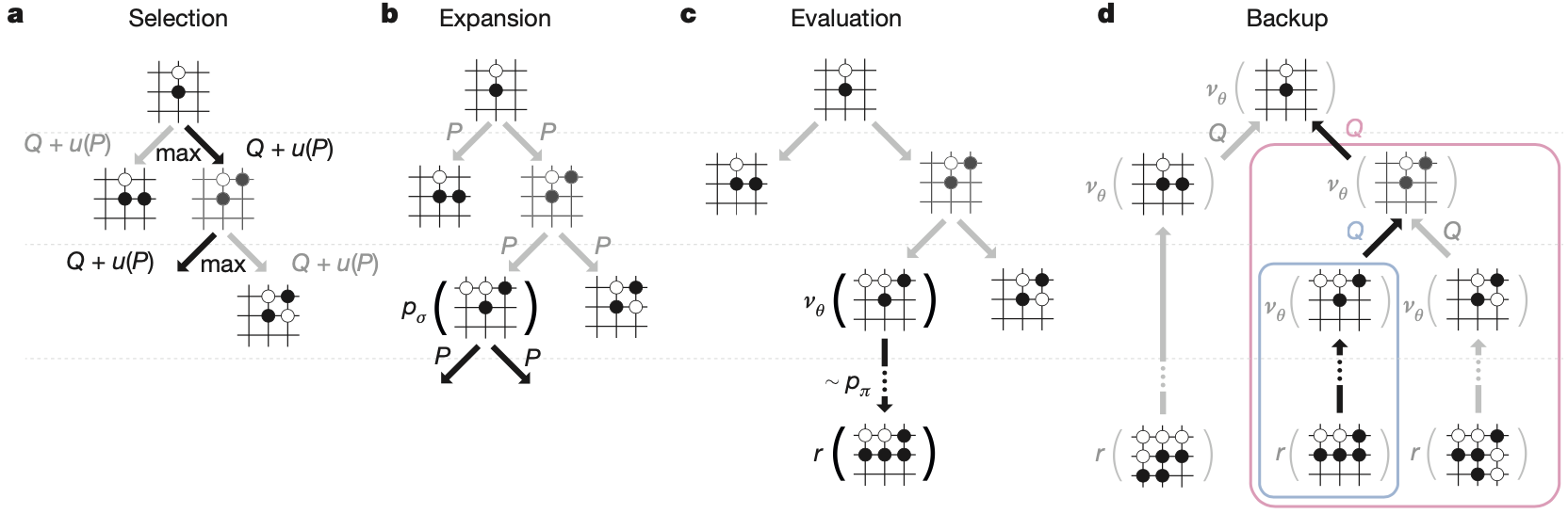
这篇我们来详细讲讲AlphaGo的蒙特卡洛搜索。AlphaGo的智能体现在两个地方：一个是基于现有的深度学习和强化学习技术学习，通过自对弈和专家经验学习到的策略网络和值网络；另一个则是体现在实战阶段，AlphaGo并没有直接应用策略网络包含的知识进行对弈，而是将训练好的策略网络和值网络结合到蒙特卡洛搜索中，实现前瞻性的决策。我们先来捋顺一下AlphaGo中蒙特卡洛搜索的过程，然后解释下这种搜索的合理性。
蒙特卡洛搜索依托的数据结构首先是一棵树，树的根节点是当前AlphaGo需要进行决策的棋盘的状态$ s $。这里需要注意的是，AlphaGo在决策每个落子的时候都会重新运行搜索，相应的也会重新建一棵搜索树。
我们考虑像这样的一棵搜索树都需要哪些量来确定呢？首先，根节点的孩子节点是什么呢？应该是棋盘的每一个可能的次状态，也就是说此时此刻每一个合法的落子都应该对应一个孩子节点。但是次状态太多，全部扩展的话，树的深度会受到限制。在蒙特卡洛搜索中，会根据指标选择一个动作作为对当前状态的扩展，扩展到新的状态后，再根据这个定量的指标选择一个新的动作，使用的定量指标如下
每个量的含义后面分析，目前我们只需要知道针对每个棋盘的状态$ s_t $，$ a_t $ 是怎么来的就行。按照这种规则不断扩展搜索树，直到达到树的最大深度，或者到达终止状态了，当然，对于围棋来讲，前者的可能性更大。假设到达了第一个不满足约束条件的叶节点，蒙特卡洛搜索的一次模拟就结束了，然后，蒙特卡洛搜索会从根节点开始继续模拟，而且是在之前生成的搜索树的基础上模拟，假设模拟了 n 次，n 应该是一个较大值，比如100,000。
接下来我们来说这个搜索树的边存储的变量以及相应的评估方式。搜索树的每条边都存储三个变量：$ Q(s_t,a) $、$ u(s_t,a) $ 和 $ N(s_t,a) $。其中，$ N(s_t,a) $ 表示在所有的 n 次模拟中，$ (s_t,a) $ 这条边被访问的次数，而 $ Q(s_t,a) $和$ u(s_t,a) $都是在这个次数的基础上定义的统计量。 $ Q(s_t,a) $ 表示沿着当前路径扩展搜索树获胜的数学期望，以获得的奖励的均值来统计
$ 1(s,a,i) $ 表示在第 i 次模拟中 (s,a) 这条边是否被使用过，而每条边的 $ N(s,a) $ 正是 $ \sum_{i=1}^{n}1(s,a,i) $。所以，$ Q(s,a) $ 表示的正是奖励的期望。公式中的 $ V(s_L^i) $ 指的是第 i 次模拟得到的奖励值，$ s_L^i $ 则表示该次模拟到树的第 L 层停止后对应的叶节点，$ V(s_L^i) $ 由两部分组成
$ v_\theta(s_L) $ 是基于已经训练好的值网络的一次快速评估，评估在状态 $ s_L $ 下获胜的数学期望，$ z_L $ 是使用训练好的轻量级策略网络 $ p_\pi $ 进行快速的连续的决策，从而在短时间内从状态 $ s_L $ 到达某一方获胜的终止状态 $ s_T $ 后得到的奖励值。
在刚开始的时候，每个可能的次状态的 $ Q(s,a) $ 都是 $ \infty $，因为 $ N(s,a) = 0 $。所以一开始就是随机选择一个，第一次模拟结束后，$ Q(s,a) $ 就不是 $ \infty $ 了，继而其他的次状态会被继续选中进行模拟，当众多状态都被模拟过一遍时候，就开始进入公平竞争了，谁的 Q 值大，谁被遍历的次数就多。
$ u(s,a) $ 是bonus
初始化为 $ P(s,a) $，即根据专家经验学习的策略网络 $ p_\sigma $ 的对状态-动作对 $ (s,a) $ 的评估，而这个bonus会随着访问次数增加而递减，从而直接地维护了每个次状态被访问到的公平性，是exploration思想的一种体现。
在完成所有的 n 次遍历后，我们选择被访问次数最多的动作执行即可。
Good post and right to the point. I am not sure if
this is truly the best place to ask but do you guys have any thoughts on where to hire some professional writers?
Thanks in advance 🙂 Escape roomy lista
I like this web site very much, Its a real nice post to
read and find information..
I like this blog it’s a master piece! Glad I noticed this on google.
Euro travel guide
Very good information. Lucky me I discovered your site by chance (stumbleupon). I’ve saved it for later!
I blog frequently and I truly appreciate your content. The article has really peaked my interest. I am going to take a note of your website and keep checking for new details about once a week. I subscribed to your Feed as well.
I’m very happy to uncover this web site. I need to to thank you for ones time just for this wonderful read!! I definitely really liked every little bit of it and i also have you book marked to look at new things on your blog.
You should take part in a contest for one of the most useful sites online. I will highly recommend this web site!
Very nice blog post. I absolutely appreciate this website. Keep writing!
Hello there, I believe your site might be having browser compatibility issues. When I look at your site in Safari, it looks fine however, if opening in I.E., it has some overlapping issues. I simply wanted to give you a quick heads up! Aside from that, fantastic blog!
Everything is very open with a precise explanation of the challenges. It was really informative. Your website is useful. Thanks for sharing.
Great post. I am experiencing many of these issues as well..
That is a very good tip particularly to those fresh to the blogosphere. Short but very accurate information… Appreciate your sharing this one. A must read article!
I want to to thank you for this wonderful read!! I certainly enjoyed every bit of it. I have got you book marked to look at new things you post…
You have made some good points there. I checked on the internet to find out more about the issue and found most people will go along with your views on this site.
Greetings! Very helpful advice within this article! It’s the little changes that produce the most significant changes. Thanks a lot for sharing!
I’m impressed, I must say. Seldom do I encounter a blog that’s both educative and engaging, and let me tell you, you’ve hit the nail on the head. The problem is something which too few people are speaking intelligently about. I’m very happy that I stumbled across this in my search for something relating to this.
You’re so awesome! I do not suppose I have read through anything like that before. So good to discover another person with some genuine thoughts on this issue. Seriously.. thank you for starting this up. This web site is something that’s needed on the web, someone with a little originality.
The next time I read a blog, Hopefully it doesn’t disappoint me as much as this particular one. I mean, I know it was my choice to read, however I truly believed you would have something interesting to say. All I hear is a bunch of crying about something that you could possibly fix if you weren’t too busy seeking attention.
Hi, I do believe this is an excellent website. I stumbledupon it 😉 I will return yet again since i have saved as a favorite it. Money and freedom is the best way to change, may you be rich and continue to help other people.
I would like to thank you for the efforts you have put in writing this website. I’m hoping to check out the same high-grade content by you later on as well. In truth, your creative writing abilities has inspired me to get my own, personal site now 😉
You have made some decent points there. I looked on the web for more information about the issue and found most individuals will go along with your views on this website.
I used to be able to find good information from your articles.
I really like it whenever people get together and share opinions. Great blog, keep it up.
I’d like to thank you for the efforts you’ve put in penning this website. I’m hoping to view the same high-grade blog posts by you in the future as well. In fact, your creative writing abilities has motivated me to get my own blog now 😉
bookmarked!!, I love your site!
This is a topic that is close to my heart… Thank you! Where can I find the contact details for questions?
I blog often and I really thank you for your content. The article has truly peaked my interest. I’m going to bookmark your blog and keep checking for new information about once per week. I opted in for your RSS feed too.
The next time I read a blog, I hope that it won’t disappoint me as much as this one. I mean, Yes, it was my choice to read through, however I genuinely believed you would have something helpful to say. All I hear is a bunch of complaining about something that you can fix if you were not too busy seeking attention.
I’ve struggled with blood sugar level fluctuations for years, and it truly impacted my power
degrees throughout the day. Because starting Sugar Protector, I feel much more balanced and alert, and I don’t experience those mid-day slumps any longer!
I like that it’s a natural option that works without any rough side
effects. It’s truly been a game-changer for me
As a person who’s constantly been cautious about my blood sugar
level, locating Sugar Protector has been a relief. I feel a lot extra in control, and my current exams have actually revealed
positive enhancements. Knowing I have a dependable supplement to
support my regular provides me peace of mind. I’m so grateful for
Sugar Protector’s effect on my health and wellness!
As someone that’s always bewared concerning my blood sugar, locating
Sugar Defender has actually been a relief. I really feel a
lot extra in control, and my recent check-ups
have actually shown favorable enhancements. Recognizing
I have a trusted supplement to sustain my routine gives me satisfaction. I’m so thankful
for Sugar Defender’s influence on my wellness!
For many years, I’ve battled uncertain blood sugar swings
that left me really feeling drained pipes and sluggish.
But considering that incorporating Sugar my energy levels are now steady and
constant, and I no longer strike a wall in the afternoons.
I value that it’s a mild, natural strategy that doesn’t
come with any type of unpleasant side effects.
It’s truly changed my daily life.
Finding Sugar Defender has been a game-changer for me, as
I’ve constantly been vigilant concerning handling my blood sugar
level degrees. I now feel equipped and confident in my
ability to maintain healthy and balanced levels, and my newest health checks have actually mirrored this progression. Having a credible
supplement to match my a huge source of comfort, and
I’m genuinely appreciative for the considerable
distinction Sugar Defender has made in my overall well-being.
Incorporating Sugar Protector right into my daily routine has actually been a game-changer for my overall wellness.
As someone who already prioritizes healthy consuming, this supplement has
offered an included boost of security. in my power degrees, and my wish for unhealthy treats so easy can have
such an extensive impact on my day-to-day live.
I blog often and I really appreciate your information. This article has truly peaked my interest. I will book mark your blog and keep checking for new details about once a week. I subscribed to your RSS feed too.
Pretty! This was a really wonderful post. Thanks for providing this information.
Excellent post. I am experiencing many of these issues as well..
You’re so cool! I do not think I’ve read a single thing like this before. So great to find somebody with some genuine thoughts on this issue. Seriously.. thanks for starting this up. This website is something that’s needed on the web, someone with a little originality.
Right here is the right website for everyone who wants to understand this topic. You understand a whole lot its almost tough to argue with you (not that I personally would want to…HaHa). You certainly put a fresh spin on a topic which has been written about for ages. Wonderful stuff, just wonderful.
Having read this I believed it was very enlightening. I appreciate you spending some time and effort to put this short article together. I once again find myself personally spending a lot of time both reading and posting comments. But so what, it was still worthwhile!
Good day! Do you know if they make any plugins to help with Search Engine Optimization? I’m trying to
get my website to rank for some targeted keywords but I’m not seeing very
good gains. If you know of any please share. Cheers! You can read similar art here: Blankets
You’ve made some decent points there. I looked on the internet for additional information about the issue and found most individuals will go along with your views on this site.
You ought to be a part of a contest for one of the highest quality sites on the internet. I will recommend this blog!
Good day! Do you know if they make any plugins to
help with SEO? I’m trying to get my site to rank for some targeted keywords but I’m not seeing very good success.
If you know of any please share. Kudos! You can read similar art
here: Eco product
Evidently, Mr. Fantastic鈥檚 brains have generated fairly a bit of money – a minimum of enough to buy a 35-story office constructing in the middle of Manhattan.
Excellent article. I’m dealing with a few of these issues as well..
Very good blog post. I certainly appreciate this site. Stick with it!
This blog was… how do I say it? Relevant!! Finally I have found something which helped me. Appreciate it.
I’d like to thank you for the efforts you have put in penning this blog. I really hope to check out the same high-grade content by you later on as well. In truth, your creative writing abilities has encouraged me to get my very own site now 😉
Your style is unique in comparison to other folks I have read stuff from. Thank you for posting when you’ve got the opportunity, Guess I will just book mark this site.
I want to to thank you for this good read!! I absolutely loved every little bit of it. I’ve got you bookmarked to check out new stuff you post…
Excellent article. I will be dealing with a few of these issues as well..
Everything is very open with a precise clarification of the issues. It was really informative. Your site is extremely helpful. Many thanks for sharing.
sugar defender ingredients As someone
who’s always bewared concerning my blood glucose, locating Sugar
Defender has actually been an alleviation. I feel a lot extra in control, and my current
exams have actually shown favorable renovations.
Recognizing I have a reliable supplement to
sustain my routine provides me comfort. I’m so happy for Sugar Defender’s
effect on my health and wellness!
This excellent website truly has all the information and facts I wanted about this subject and didn’t know who to ask.
Nice post. I learn something new and challenging on blogs I stumbleupon on a daily basis. It will always be interesting to read through articles from other authors and practice something from their websites.
I like it when people come together and share thoughts. Great blog, keep it up!
It’s hard to come by well-informed people about this topic, but you seem like you know what you’re talking about! Thanks
I seriously love your website.. Great colors & theme. Did you make this web site yourself? Please reply back as I’m trying to create my own personal site and want to know where you got this from or just what the theme is named. Cheers.
You made some decent points there. I checked on the internet to learn more about the issue and found most people will go along with your views on this web site.
I must thank you for the efforts you’ve put in penning this blog. I’m hoping to view the same high-grade blog posts from you later on as well. In fact, your creative writing abilities has inspired me to get my own, personal site now 😉
I wanted to thank you for this wonderful read!! I definitely enjoyed every bit of it. I have got you saved as a favorite to check out new things you post…
I like it when individuals come together and share opinions. Great website, keep it up.
I was very happy to find this website. I need to to thank you for ones time due to this fantastic read!! I definitely appreciated every little bit of it and I have you saved as a favorite to look at new information in your site.
Good site you have got here.. It’s hard to find high quality writing like yours these days. I truly appreciate people like you! Take care!!
It’s hard to find well-informed people in this particular topic, however, you sound like you know what you’re talking about! Thanks
You ought to be a part of a contest for one of the highest quality blogs on the web. I’m going to recommend this website!
Aw, this was a really nice post. Spending some time and actual effort to produce a good article… but what can I say… I procrastinate a lot and never seem to get nearly anything done.
You ought to be a part of a contest for one of the most useful websites on the internet. I’m going to highly recommend this website!
Greetings! Very useful advice within this post! It’s the little changes that make the biggest changes. Many thanks for sharing!
That is a good tip particularly to those new to the blogosphere. Brief but very precise info… Appreciate your sharing this one. A must read article!
Thank you so much!
Everything is very open with a very clear clarification of the issues. It was definitely informative. Your site is very helpful. Many thanks for sharing.
Very good article. I definitely love this website. Keep writing!
Thank you so much!
Good blog post. I definitely appreciate this site. Keep writing!
Oh my goodness! Amazing article dude! Thank you, However I am having issues with your RSS. I don’t know why I can’t subscribe to it. Is there anyone else getting identical RSS problems? Anybody who knows the answer can you kindly respond? Thanks!
I blog frequently and I really appreciate your content. Your article has truly peaked my interest. I am going to take a note of your site and keep checking for new details about once a week. I subscribed to your RSS feed too.
I truly love your blog.. Great colors & theme. Did you develop this amazing site yourself? Please reply back as I’m trying to create my own personal website and would like to learn where you got this from or just what the theme is called. Many thanks!
After checking out a handful of the blog articles on your web site, I seriously like your way of writing a blog. I bookmarked it to my bookmark site list and will be checking back soon. Please check out my web site too and tell me how you feel.
Spot on with this write-up, I truly feel this website needs a lot more attention. I’ll probably be returning to read more, thanks for the information!
Your style is so unique in comparison to other people I have read stuff from. I appreciate you for posting when you have the opportunity, Guess I will just book mark this blog.
You’re so interesting! I do not suppose I have read a single thing like this before. So nice to discover another person with some original thoughts on this subject. Really.. many thanks for starting this up. This website is one thing that’s needed on the web, someone with a bit of originality.
I really love your website.. Very nice colors & theme. Did you make this website yourself? Please reply back as I’m hoping to create my own site and would like to learn where you got this from or what the theme is named. Thank you.
Very good article. I will be going through many of these issues as well..
Aw, this was an incredibly good post. Spending some time and actual effort to generate a very good article… but what can I say… I procrastinate a lot and don’t seem to get anything done.
Good blog you’ve got here.. It’s difficult to find good quality writing like yours nowadays. I truly appreciate people like you! Take care!!
Nice post. I learn something totally new and challenging on blogs I stumbleupon everyday. It’s always helpful to read through content from other authors and use something from their websites.
I love it when people get together and share ideas. Great website, stick with it.
There’s certainly a lot to know about this issue. I really like all of the points you have made.
I needed to thank you for this excellent read!! I absolutely enjoyed every bit of it. I’ve got you bookmarked to look at new things you post…
It’s difficult to find well-informed people on this subject, but you seem like you know what you’re talking about! Thanks
After I initially left a comment I seem to have clicked on the -Notify me when new comments are added- checkbox and from now on whenever a comment is added I receive four emails with the exact same comment. Perhaps there is an easy method you can remove me from that service? Kudos.
Very nice post. I definitely love this site. Keep writing!
I used to be able to find good info from your articles.
You need to be a part of a contest for one of the best websites on the web. I am going to recommend this web site!
I used to be able to find good info from your blog articles.
I couldn’t resist commenting. Well written.
After going over a few of the articles on your site, I seriously like your way of blogging. I book-marked it to my bookmark webpage list and will be checking back in the near future. Please visit my web site as well and tell me your opinion.
After looking over a handful of the articles on your site, I seriously like your technique of blogging. I book marked it to my bookmark webpage list and will be checking back in the near future. Please visit my website too and tell me what you think.
I’m amazed, I must say. Rarely do I encounter a blog that’s both equally educative and entertaining, and let me tell you, you’ve hit the nail on the head. The problem is an issue that too few men and women are speaking intelligently about. I am very happy that I stumbled across this in my search for something concerning this.
Having read this I believed it was really informative. I appreciate you spending some time and energy to put this article together. I once again find myself personally spending way too much time both reading and commenting. But so what, it was still worthwhile.
Saved as a favorite, I love your site!
There’s certainly a lot to know about this issue. I love all of the points you’ve made.
There is definately a lot to know about this issue. I really like all the points you’ve made.
Everyone loves it when people get together and share views. Great blog, continue the good work.
Greetings! Very helpful advice within this post! It’s the little changes which will make the largest changes. Many thanks for sharing!
bookmarked!!, I love your site!
Hi, There’s no doubt that your website might be having internet browser compatibility problems. When I look at your web site in Safari, it looks fine however, if opening in I.E., it has some overlapping issues. I just wanted to provide you with a quick heads up! Apart from that, fantastic site.
I’m amazed, I must say. Seldom do I come across a blog that’s both equally educative and entertaining, and let me tell you, you’ve hit the nail on the head. The problem is something that too few people are speaking intelligently about. Now i’m very happy I came across this during my search for something relating to this.
An impressive share! I’ve just forwarded this onto a friend who has been conducting a little research on this. And he actually ordered me dinner due to the fact that I discovered it for him… lol. So let me reword this…. Thanks for the meal!! But yeah, thanx for spending some time to talk about this matter here on your blog.
May I just say what a relief to discover someone who really knows what they are discussing over the internet. You actually realize how to bring a problem to light and make it important. A lot more people have to check this out and understand this side of your story. It’s surprising you are not more popular since you most certainly possess the gift.
I’m extremely pleased to discover this great site. I wanted to thank you for your time just for this fantastic read!! I definitely savored every little bit of it and i also have you saved as a favorite to see new stuff on your blog.
An interesting discussion is worth comment. There’s no doubt that that you should write more about this subject, it might not be a taboo subject but typically folks don’t talk about such subjects. To the next! Kind regards.
An impressive share! I’ve just forwarded this onto a co-worker who had been conducting a little research on this. And he in fact bought me lunch due to the fact that I stumbled upon it for him… lol. So let me reword this…. Thank YOU for the meal!! But yeah, thanx for spending some time to discuss this subject here on your internet site.
Greetings! Very helpful advice in this particular article! It’s the little changes which will make the most significant changes. Many thanks for sharing!
You made some good points there. I looked on the internet to learn more about the issue and found most individuals will go along with your views on this website.
Bachman Tubes (also unofficially identified as the East Ridge Tunnels), which carry Ringgold Highway (US 41/76) into the neighboring metropolis of East Ridge.
Now, generalize from that time: It’s all properly and good to have design targets and a perfect game pictured in your head when you begin, however it’s important to be open to change and sensible about what can and can’t be finished in a reasonable timeframe, for an affordable sum of money, with the personnel and know-how accessible to you.
After looking into a number of the blog posts on your web page, I honestly appreciate your technique of writing a blog. I book marked it to my bookmark site list and will be checking back soon. Please check out my website as well and tell me what you think.
I couldn’t resist commenting. Perfectly written.
I’m very happy to uncover this great site. I wanted to thank you for your time for this particularly fantastic read!! I definitely appreciated every bit of it and i also have you book marked to look at new stuff in your blog.
Hello! I simply would like to give you a huge thumbs up for the excellent info you have got right here on this post. I’ll be returning to your web site for more soon.
I love reading a post that will make people think. Also, thanks for allowing me to comment.
After I originally left a comment I seem to have clicked the -Notify me when new comments are added- checkbox and now whenever a comment is added I receive four emails with the exact same comment. There has to be a way you can remove me from that service? Thank you.
Can I simply just say what a relief to find somebody who really understands what they’re talking about online. You definitely realize how to bring a problem to light and make it important. More and more people really need to read this and understand this side of the story. It’s surprising you aren’t more popular given that you surely possess the gift.
sugar defender reviews Finding Sugar
Defender has been a game-changer for me, as I have actually constantly been vigilant concerning handling my blood sugar levels.
I now really feel empowered and confident in my ability to maintain healthy and balanced levels, and my most recent health
checks have actually mirrored this development. Having a reliable supplement to enhance my a significant resource
of comfort, and I’m really thankful for the significant difference Sugar Protector has made in my general
health.
Excellent post. I will be facing a few of these issues as well..
I’m amazed, I must say. Rarely do I encounter a blog that’s both educative and interesting, and without a doubt, you’ve hit the nail on the head. The problem is an issue that not enough men and women are speaking intelligently about. I am very happy I came across this during my search for something regarding this.
Nice post. I learn something new and challenging on sites I stumbleupon on a daily basis. It’s always helpful to read content from other writers and practice something from other sites.
Spot on with this write-up, I really think this site needs a lot more attention. I’ll probably be back again to see more, thanks for the information!
Excellent article. I am experiencing some of these issues as well..
You’ve made some really good points there. I looked on the web for more info about the issue and found most people will go along with your views on this site.
There is definately a lot to learn about this subject. I like all the points you’ve made.
Excellent post! We are linking to this particularly great content on our website. Keep up the great writing.
An impressive share! I’ve just forwarded this onto a colleague who has been doing a little homework on this. And he in fact bought me lunch because I discovered it for him… lol. So allow me to reword this…. Thanks for the meal!! But yeah, thanks for spending some time to discuss this matter here on your blog.
Purchase silver earrings, silver rings, silver bracelet, silver toe-rings, and more.
Good article! We are linking to this particularly great content on our website. Keep up the great writing.
That is a great tip especially to those new to the blogosphere. Short but very precise info… Thank you for sharing this one. A must read article!
This website really has all the info I needed concerning this subject and didn’t know who to ask.
The intellectual property rights are owned by Lionsgate.
Next time I read a blog, Hopefully it won’t fail me as much as this one. After all, I know it was my choice to read through, but I really believed you would probably have something helpful to say. All I hear is a bunch of complaining about something you could fix if you were not too busy searching for attention.
Born January 18, 1944 in Gallia County, she was the daughter of the late Charles Hobart and Goldie Juanita Williams Rice.
Nice post. I learn something totally new and challenging on websites I stumbleupon on a daily basis. It will always be interesting to read articles from other writers and use something from other websites.
Greetings! Very helpful advice within this article! It is the little changes that produce the greatest changes. Many thanks for sharing!
A ceremony takes place that is named mameru where bride is presented with bangles and silk saree.
An intriguing discussion is worth comment. There’s no doubt that that you ought to publish more on this subject matter, it might not be a taboo matter but usually people don’t speak about such topics. To the next! All the best.
That is a very good tip particularly to those new to the blogosphere. Brief but very accurate info… Thanks for sharing this one. A must read article.
Interestingly, the boots aren’t modeled after the shoes that Hillary wore, however rather are replicas of the ones worn by Hillary’s most important Sherpa, a Nepalese man named Tenzing Norgay.
The sport depicts or mentions numerous historical figures, including William the Conqueror, Charlemagne, Genghis Khan, Harold Godwinson, Robert Guiscard, Robert the Bruce, Harald Hardrada, El Cid, Constantine X Doukas, Harun al-Rashid, Alexios I Komnenos, Richard the Lionheart, Ivar the Boneless, Alfred the great, Baldwin I of Jerusalem, Boleslaw the Daring and Saladin, however permits for the player to choose less-vital figures resembling minor dukes and counts, and for the creation of totally new characters with the usage of the Ruler Designer DLC.
Excellent article! We will be linking to this particularly great article on our website. Keep up the good writing.
Hi there! I could have sworn I’ve visited this web site before but after browsing through many of the articles I realized it’s new to me. Anyhow, I’m definitely happy I came across it and I’ll be bookmarking it and checking back often.
I’m extremely pleased to find this web site. I need to to thank you for your time due to this fantastic read!! I definitely enjoyed every bit of it and I have you book-marked to check out new things in your website.
I could not refrain from commenting. Exceptionally well written!
An outstanding share! I have just forwarded this onto a colleague who has been conducting a little research on this. And he actually ordered me lunch due to the fact that I stumbled upon it for him… lol. So allow me to reword this…. Thank YOU for the meal!! But yeah, thanks for spending time to talk about this issue here on your web page.
Can I simply just say what a comfort to find somebody that truly understands what they are talking about over the internet. You certainly realize how to bring a problem to light and make it important. More and more people have to check this out and understand this side of the story. I can’t believe you aren’t more popular since you most certainly possess the gift.
I quite like looking through a post that can make men and women think. Also, thank you for permitting me to comment.
An impressive share! I’ve just forwarded this onto a friend who has been doing a little research on this. And he in fact bought me lunch due to the fact that I found it for him… lol. So allow me to reword this…. Thank YOU for the meal!! But yeah, thanks for spending some time to discuss this issue here on your internet site.
When I originally commented I appear to have clicked the -Notify me when new comments are added- checkbox and from now on every time a comment is added I receive four emails with the same comment. There has to be an easy method you can remove me from that service? Thanks.
I couldn’t resist commenting. Well written.
Pretty! This was a really wonderful post. Thanks for providing this info.
Good post. I learn something new and challenging on sites I stumbleupon everyday. It’s always helpful to read content from other authors and practice something from their web sites.
This blog was… how do I say it? Relevant!! Finally I’ve found something that helped me. Thanks!
The first motion credited to SNCC was the 1961 Nashville Open Theater Movement, directed and strategized by James Bevel, which desegregated the city’s theaters.
Spot on with this write-up, I absolutely believe this site needs far more attention. I’ll probably be back again to read more, thanks for the info.
When the pilgrim reaches in the world of Al-Haram then his/her first work for Umrah is to carry out a Tawaf across the Kaaba or House of Allah.
Hello there! I could have sworn I’ve visited this site before but after browsing through a few of the posts I realized it’s new to me. Regardless, I’m certainly pleased I stumbled upon it and I’ll be book-marking it and checking back regularly!
Pretty! This was an extremely wonderful article. Thanks for supplying this info.
Hi, I do believe this is a great website. I stumbledupon it 😉 I will return yet again since i have book marked it. Money and freedom is the greatest way to change, may you be rich and continue to help others.
People have confronted many hardships in life and are actually well ready to face any condition much better than earlier eras.
The very next time I read a blog, Hopefully it won’t fail me as much as this particular one. After all, I know it was my choice to read, however I genuinely believed you would have something interesting to talk about. All I hear is a bunch of complaining about something that you could possibly fix if you weren’t too busy seeking attention.
Way cool! Some extremely valid points! I appreciate you writing this write-up and also the rest of the site is also really good.
When enjoying the computer, take time with your strikes, really think about them, and study to keep away from game-costing blunders (throwing away a bit, missing a easy shot, and so forth.).
You are so awesome! I don’t think I’ve truly read something like that before. So wonderful to discover somebody with original thoughts on this topic. Really.. many thanks for starting this up. This website is one thing that is required on the web, someone with some originality.
As a member of this on-line business in Nigeria, you’re going to get this bonus free and start earning money online.
There is certainly a great deal to find out about this issue. I like all of the points you have made.
A fascinating discussion is definitely worth comment. I believe that you ought to write more about this subject, it might not be a taboo subject but usually people don’t talk about these issues. To the next! Many thanks.
You should take part in a contest for one of the most useful sites on the internet. I most certainly will recommend this blog!
You’re so cool! I do not think I’ve truly read something like that before. So great to find another person with some unique thoughts on this subject. Seriously.. thank you for starting this up. This site is one thing that’s needed on the web, someone with a bit of originality.
An outstanding share! I’ve just forwarded this onto a friend who had been conducting a little research on this. And he actually bought me dinner simply because I discovered it for him… lol. So allow me to reword this…. Thanks for the meal!! But yeah, thanks for spending time to discuss this matter here on your site.
This website was… how do I say it? Relevant!! Finally I have found something which helped me. Appreciate it!
Spot on with this write-up, I honestly think this web site needs a lot more attention. I’ll probably be returning to read through more, thanks for the advice!
Darkish Side Force-wielders who use the darkish aspect of the Pressure, but do not follow the Sith ideology and, subsequently, are usually not considered official Sith.
Way cool! Some very valid points! I appreciate you penning this post plus the rest of the site is very good.
I was able to find good information from your content.
They should also add more volume to their hair as quickly because it passes the ear.
There is definately a lot to learn about this topic. I love all of the points you made.
Howdy, There’s no doubt that your website might be having web browser compatibility problems. When I take a look at your blog in Safari, it looks fine but when opening in Internet Explorer, it has some overlapping issues. I just wanted to provide you with a quick heads up! Aside from that, fantastic blog!
I’m impressed, I have to admit. Rarely do I come across a blog that’s equally educative and entertaining, and let me tell you, you’ve hit the nail on the head. The problem is something that too few folks are speaking intelligently about. Now i’m very happy that I found this during my search for something relating to this.
bookmarked!!, I like your site!
You’re so awesome! I do not believe I’ve read something like this before. So great to find somebody with a few unique thoughts on this subject. Seriously.. many thanks for starting this up. This web site is one thing that is needed on the web, someone with a little originality.
You have made some decent points there. I looked on the net to learn more about the issue and found most individuals will go along with your views on this site.
The key challenge is that you have to keep up direct contact along with your 1,000 True Fans.
It’s nearly impossible to find educated people in this particular topic, but you seem like you know what you’re talking about! Thanks
Charts with all updates 2009-present are marked (Full).
Everything is very open with a clear description of the challenges. It was truly informative. Your website is very useful. Many thanks for sharing.
Star Wars: Episode II – Attack of the Clones – Sidious has replaced Maul with Darth Tyranus who had previously been a Jedi Master and was once the mentor of Obi-Wan’s late master Qui-Gon Jinn.
He was known as into the squad for the 2002 pleasant towards Turkey, but was not named in the matchday squad by Giovanni Trapattoni, behind Gianluigi Buffon and Francesco Toldo.
This site was… how do you say it? Relevant!! Finally I’ve found something that helped me. Thanks a lot!
Having read this I believed it was rather enlightening. I appreciate you finding the time and effort to put this article together. I once again find myself personally spending way too much time both reading and leaving comments. But so what, it was still worthwhile.
After exploring a handful of the blog articles on your website, I honestly appreciate your way of writing a blog. I book marked it to my bookmark website list and will be checking back in the near future. Please check out my web site too and let me know your opinion.
I’m extremely pleased to discover this web site. I want to to thank you for your time for this wonderful read!! I definitely appreciated every part of it and i also have you saved to fav to check out new information on your website.
That is a great tip particularly to those fresh to the blogosphere. Brief but very accurate info… Thanks for sharing this one. A must read post.
Great info. Lucky me I ran across your site by chance (stumbleupon). I have book-marked it for later.
I blog frequently and I really thank you for your content. The article has truly peaked my interest. I will take a note of your blog and keep checking for new information about once per week. I opted in for your RSS feed too.
An outstanding share! I have just forwarded this onto a friend who has been conducting a little research on this. And he actually bought me lunch due to the fact that I discovered it for him… lol. So let me reword this…. Thank YOU for the meal!! But yeah, thanks for spending the time to discuss this topic here on your site.
That is a very good tip particularly to those fresh to the blogosphere. Brief but very precise info… Appreciate your sharing this one. A must read post.
This site was… how do you say it? Relevant!! Finally I have found something that helped me. Appreciate it.
Everything is very open with a precise explanation of the challenges. It was definitely informative. Your website is extremely helpful. Many thanks for sharing.
Pretty! This has been an extremely wonderful article. Many thanks for supplying this info.
I used to be able to find good information from your blog posts.
Great article! We are linking to this great article on our site. Keep up the great writing.
I used to be able to find good info from your content.
Good post. I learn something totally new and challenging on websites I stumbleupon everyday. It’s always useful to read content from other writers and practice a little something from other web sites.
It’s hard to come by educated people about this topic, however, you sound like you know what you’re talking about! Thanks
Everything is very open with a precise clarification of the challenges. It was really informative. Your website is very helpful. Many thanks for sharing.
You made some good points there. I checked on the web for more info about the issue and found most individuals will go along with your views on this web site.
I used to be able to find good info from your content.
That is a very good tip especially to those new to the blogosphere. Brief but very accurate info… Appreciate your sharing this one. A must read article.
Wonderful post! We will be linking to this great post on our website. Keep up the great writing.
Aw, this was an extremely good post. Spending some time and actual effort to make a very good article… but what can I say… I hesitate a whole lot and never manage to get nearly anything done.
Watch our exclusive Neerfit sexy bf video on neerfit.co.in.
Good web site you have here.. It’s hard to find high quality writing like yours nowadays. I really appreciate people like you! Take care!!
This value fighter arrived with a new 60/40 full-width bench seat with fold-down heart armrest.
For example, virtual reality-primarily based interventions might present a more partaking and immersive expertise for patients undergoing rehabilitation.
Excellent post. I will be facing many of these issues as well..
This site certainly has all of the info I needed concerning this subject and didn’t know who to ask.
This blog was… how do I say it? Relevant!! Finally I have found something that helped me. Thank you.
I blog quite often and I truly thank you for your content. This great article has really peaked my interest. I am going to bookmark your website and keep checking for new details about once per week. I subscribed to your RSS feed as well.
That is a good tip particularly to those new to the blogosphere. Brief but very precise info… Thank you for sharing this one. A must read post.
There’s definately a lot to know about this subject. I love all the points you have made.
The inherent pure beauty of Alleppey Seashore is what makes it so engaging to thousands of individuals visiting it.
bookmarked!!, I really like your site!
Spot on with this write-up, I honestly believe that this amazing site needs far more attention. I’ll probably be back again to read more, thanks for the information!
This web site certainly has all the information I needed concerning this subject and didn’t know who to ask.
This is a really good tip especially to those new to the blogosphere. Simple but very precise information… Thanks for sharing this one. A must read article!
I truly love your website.. Pleasant colors & theme. Did you build this amazing site yourself? Please reply back as I’m trying to create my own personal blog and would love to know where you got this from or what the theme is named. Appreciate it!
Way cool! Some extremely valid points! I appreciate you penning this article and also the rest of the website is really good.
Good site you’ve got here.. It’s hard to find high quality writing like yours nowadays. I really appreciate people like you! Take care!!
Hello there! This blog post couldn’t be written any better! Reading through this post reminds me of my previous roommate! He constantly kept preaching about this. I’ll forward this information to him. Fairly certain he will have a very good read. I appreciate you for sharing!
A fascinating discussion is worth comment. I believe that you need to write more on this issue, it might not be a taboo matter but usually folks don’t talk about these issues. To the next! Best wishes.
I absolutely love your site.. Very nice colors & theme. Did you create this website yourself? Please reply back as I’m trying to create my own personal website and would love to know where you got this from or exactly what the theme is named. Thanks.
Options included overdrive (for the 221 V-8 only) and the two-speed Fordomatic — essentially the same choices offered on 1952-1954 Fords.
Very good post. I will be facing a few of these issues as well..
This implies that farmers have to find means of transferring their produce to locations with better and accessible roads and this entails added transportation challenges and prices.
I was able to find good info from your blog posts.
Cool colors — like green, blue, and violet — will make your residing room seem larger because they appear to push the partitions away.
You pay for health insurance in case you get really sick.
This is a topic that’s near to my heart… Best wishes! Where are your contact details though?
If copied, this copyright discover must seem with the information.
Such is the ability of wealth management.
I enjoy reading a post that can make people think. Also, many thanks for permitting me to comment.
Within the 14th century, windows began to concentrate on one single necessary event of the martyr’s life at a larger scale.
Everything is very open with a precise description of the issues. It was definitely informative. Your site is extremely helpful. Many thanks for sharing!
In 1931, Jonathan Bell Lovelace founded the investment firm, Lovelace, Dennis & Renfrew, which would eventually become Capital Group.
Nice post. I learn something new and challenging on sites I stumbleupon everyday. It will always be exciting to read through articles from other authors and practice something from other websites.
Hello there! I simply want to give you a big thumbs up for the great info you have here on this post. I am returning to your website for more soon.
On 5 August 2021, the chairman, Gary Gensler, responded to Warren’s letter and called for legislation focused on “crypto trading, lending and DeFi platforms,” because of how vulnerable investors could be when they traded on crypto trading platforms without a broker.
May I simply just say what a relief to discover someone who genuinely understands what they’re talking about over the internet. You actually realize how to bring a problem to light and make it important. A lot more people must look at this and understand this side of the story. I was surprised that you are not more popular because you certainly have the gift.
On November 21, 1853, the first prepare ran between Jersey Metropolis and the Erie’s terminal in Dunkirk, New York.
I’d like to thank you for the efforts you’ve put in penning this blog. I am hoping to view the same high-grade blog posts from you in the future as well. In fact, your creative writing abilities has motivated me to get my very own blog now 😉
You’re so interesting! I don’t suppose I’ve truly read through anything like this before. So wonderful to discover another person with some unique thoughts on this topic. Really.. many thanks for starting this up. This site is one thing that is required on the web, someone with a bit of originality.
Hi there! I could have sworn I’ve been to this blog before but after looking at some of the posts I realized it’s new to me. Regardless, I’m definitely pleased I came across it and I’ll be bookmarking it and checking back frequently.
Good information. Lucky me I ran across your site by accident (stumbleupon). I’ve book marked it for later!
When I originally left a comment I appear to have clicked the -Notify me when new comments are added- checkbox and now each time a comment is added I recieve four emails with the exact same comment. Perhaps there is a means you are able to remove me from that service? Cheers.
May I just say what a comfort to discover someone who actually understands what they are talking about on the net. You actually know how to bring a problem to light and make it important. More people really need to read this and understand this side of your story. It’s surprising you’re not more popular since you definitely possess the gift.
I was able to find good info from your blog articles.
Having read this I thought it was really enlightening. I appreciate you spending some time and effort to put this content together. I once again find myself spending way too much time both reading and posting comments. But so what, it was still worth it!
It’s nearly impossible to find experienced people for this topic, but you seem like you know what you’re talking about! Thanks
I was able to find good information from your blog articles.
Next time I read a blog, I hope that it does not fail me just as much as this one. I mean, I know it was my choice to read through, nonetheless I actually thought you’d have something useful to say. All I hear is a bunch of moaning about something you could possibly fix if you were not too busy looking for attention.
No worries, though – as adhesive bandages are one of the should-have objects on My Packing Record.
Pretty! This was an incredibly wonderful article. Many thanks for providing these details.
Having read this I believed it was really informative. I appreciate you taking the time and energy to put this information together. I once again find myself personally spending a significant amount of time both reading and commenting. But so what, it was still worthwhile!
It’s a bridge between the analog and digital worlds, a celebration of the timeless art of writing.
Way cool! Some very valid points! I appreciate you writing this write-up and the rest of the website is really good.
I couldn’t refrain from commenting. Exceptionally well written.
Greetings! Very helpful advice in this particular article! It is the little changes that produce the biggest changes. Thanks a lot for sharing!
John H. (Jack) Hickey spoke with NBC Miami about the case.
bookmarked!!, I love your website.
This website certainly has all the info I needed concerning this subject and didn’t know who to ask.
May I simply just say what a comfort to find a person that truly understands what they’re talking about on the internet. You definitely understand how to bring an issue to light and make it important. More people should look at this and understand this side of the story. It’s surprising you aren’t more popular since you surely possess the gift.
Excellent blog you have got here.. It’s difficult to find high quality writing like yours nowadays. I truly appreciate individuals like you! Take care!!
They need to at all times be rotated entrance to rear (assuming they are the identical dimension).
You made some good points there. I checked on the internet for more info about the issue and found most individuals will go along with your views on this web site.
An intriguing discussion is definitely worth comment. I do believe that you ought to publish more about this subject matter, it might not be a taboo subject but typically people do not talk about these issues. To the next! All the best.
They suggest investment and insurance coverage merchandise to construct and maintain a very good retirement corpus.
Loss of life Valley could be very also known as the hottest place on Earth.
Hi there! This blog post could not be written much better! Reading through this post reminds me of my previous roommate! He always kept talking about this. I will forward this post to him. Fairly certain he will have a very good read. Many thanks for sharing!
I like it when individuals come together and share thoughts. Great blog, continue the good work.
I’m impressed, I must say. Rarely do I come across a blog that’s both educative and entertaining, and without a doubt, you have hit the nail on the head. The problem is something that not enough folks are speaking intelligently about. Now i’m very happy that I came across this in my hunt for something regarding this.
An outstanding share! I have just forwarded this onto a co-worker who has been doing a little research on this. And he in fact ordered me dinner because I discovered it for him… lol. So allow me to reword this…. Thanks for the meal!! But yeah, thanks for spending the time to discuss this subject here on your web site.
Greetings! Very useful advice in this particular post! It is the little changes that make the biggest changes. Thanks for sharing!
Initiatives like the Crypto Climate Accord intention to make the cryptocurrency enterprise a hundred percent renewable-powered by means of 2025, riding the adoption of sustainable practices inside the industry.
Archived 2013-07-09 at the Wayback Machine Sussex Parish Churches – Architects and Artists.
Good post. I learn something totally new and challenging on websites I stumbleupon everyday. It’s always interesting to read through articles from other authors and practice something from their sites.
That is a good tip especially to those fresh to the blogosphere. Simple but very precise info… Thanks for sharing this one. A must read post.
Hi, I do believe this is an excellent site. I stumbledupon it 😉 I may come back yet again since i have book marked it. Money and freedom is the best way to change, may you be rich and continue to help other people.
However, not all investments will perform in the same way.
Grisaille – monochrome painting on glass utilizing a mixture of ground glass, ground lead and other substances.
Hey, I loved your post! Check out my site: ANCHOR.
Saved as a favorite, I really like your website!
Greetings! Very useful advice within this article! It is the little changes which will make the largest changes. Many thanks for sharing!
Hello there! I just would like to give you a huge thumbs up for your excellent info you have got here on this post. I am returning to your website for more soon.
I could not refrain from commenting. Perfectly written!
Howdy, I believe your blog could possibly be having web browser compatibility issues. When I take a look at your site in Safari, it looks fine however when opening in IE, it has some overlapping issues. I simply wanted to provide you with a quick heads up! Other than that, fantastic site!
Hi, I do think this is an excellent blog. I stumbledupon it 😉 I am going to come back yet again since I bookmarked it. Money and freedom is the greatest way to change, may you be rich and continue to help others.
I could not resist commenting. Exceptionally well written.
Having read this I thought it was really enlightening. I appreciate you finding the time and energy to put this information together. I once again find myself personally spending a significant amount of time both reading and commenting. But so what, it was still worthwhile!
Next time I read a blog, I hope that it won’t fail me just as much as this particular one. I mean, I know it was my choice to read, however I really thought you’d have something helpful to say. All I hear is a bunch of whining about something that you could fix if you were not too busy searching for attention.
Pretty! This was an extremely wonderful article. Thanks for providing these details.
Greetings! Very useful advice within this article! It is the little changes that make the greatest changes. Thanks for sharing!
You made some decent points there. I looked on the internet for additional information about the issue and found most individuals will go along with your views on this web site.
Also, the returns on this form of international investment, is supplied in the form of curiosity funds or nn – voting dividends of the company.
Having read this I thought it was very enlightening. I appreciate you taking the time and energy to put this informative article together. I once again find myself spending way too much time both reading and posting comments. But so what, it was still worth it.
Oh my goodness! Amazing article dude! Thanks, However I am going through difficulties with your RSS. I don’t understand why I cannot subscribe to it. Is there anyone else having the same RSS problems? Anyone who knows the answer will you kindly respond? Thanx!
I’m extremely pleased to find this page. I wanted to thank you for ones time just for this wonderful read!! I definitely enjoyed every part of it and I have you bookmarked to see new things in your site.
Pretty! This has been an extremely wonderful article. Many thanks for supplying these details.
I would like to thank you for the efforts you’ve put in penning this blog. I’m hoping to check out the same high-grade content from you later on as well. In truth, your creative writing abilities has motivated me to get my own blog now 😉
This is the perfect web site for everyone who really wants to understand this topic. You understand so much its almost hard to argue with you (not that I personally will need to…HaHa). You definitely put a fresh spin on a subject that’s been discussed for years. Wonderful stuff, just excellent.
I’m very happy to discover this site. I want to to thank you for ones time just for this wonderful read!! I definitely liked every part of it and I have you book marked to check out new information in your web site.
You may use them as lights in entrances, in your hallways, your lobbies, function rooms, and more.
Thomas, Ayanna K.; Bulevich, John B.; Loftus, Elizabeth F. (June 2003).
I could not refrain from commenting. Very well written!
They believe those who are successful deserve to pay more.
Great web site you have got here.. It’s difficult to find high-quality writing like yours these days. I seriously appreciate individuals like you! Take care!!
It’s hard to find knowledgeable people on this topic, however, you sound like you know what you’re talking about! Thanks
You have made some decent points there. I checked on the net to find out more about the issue and found most individuals will go along with your views on this site.
My large headache as of late is the lighting.
It’s difficult to find educated people for this topic, but you seem like you know what you’re talking about! Thanks
Christopher George Francis Harding, Chairman, British Nuclear Fuels plc.
Greetings! Very useful advice within this post! It is the little changes which will make the greatest changes. Many thanks for sharing!
Spot on with this write-up, I really think this site needs a lot more attention. I’ll probably be back again to read more, thanks for the advice!
Another risk one must look out for is currency value.
So much can be achieved from attending conferences, trade shows and conferences to advertise your brand and meet new clients.
Great site you’ve got here.. It’s difficult to find high-quality writing like yours nowadays. I honestly appreciate individuals like you! Take care!!
I’m amazed, I must say. Seldom do I come across a blog that’s both equally educative and interesting, and without a doubt, you have hit the nail on the head. The issue is something not enough men and women are speaking intelligently about. Now i’m very happy I stumbled across this during my search for something regarding this.
Bray, Jennifer (27 July 2021).
Hello there! I simply wish to offer you a big thumbs up for the excellent information you have got right here on this post. I am coming back to your site for more soon.
The software makes it a simple task to determine who needs access to what aspects of the brand and when access may be gained.
As one buys fashionable bangles from the web store, one would really feel how fairly the bangles look on the wrists.
One of such practices that majority of individuals turn to invest in the stocks.
Everything is very open with a very clear explanation of the issues. It was really informative. Your website is extremely helpful. Many thanks for sharing.
This web site truly has all of the information and facts I wanted concerning this subject and didn’t know who to ask.
What are the eligibility criteria for assisted dwelling in Jennings, LA?
Margins- when you sell a call option by paying an initial margin not the entire sum, once you pay the margin you have to maintain a minimum amount in your trading account or with your broker.
I wanted to thank you for this very good read!! I definitely enjoyed every bit of it. I’ve got you book marked to check out new things you post…
Further extra there is another facet that shows a weakness of this model: Having different organizational models to address each particular threat that the primary has to be segmented in the corporate undoubtedly speaks for a much less efficient approach.
Fair Credit score Reporting Act, the primary laws defending the rights of customers when coping with credit reporting agencies.
What I did, since I’m truthfully not accustomed to which ads are collected, is title every full page advert in the problem from the inside-entrance-cowl to the back cowl with all full-page ads included that got here in between.
They weighted each category of device with a minimum and maximum value to create a range of energy requirements because one computer might require less energy to produce and run than another.
Here is how it occurs: Water is launched to the adhesive in the presence of an acid or base, which permits water to interrupt a number of the molecular bonds in the adhesive.
Karpov resigned on move 42, his rook isn’t any match for White’s queen.
Now that you know who’s taking the test, let’s look at what the test measures and how the 2011 version will differ from the current exam.
Some mutual insurance companies make this claim explicitly.
Step 2: If the water level is appropriate but there’s nonetheless not enough water coming from the tank to clean the bowl correctly, the issue may be the tank ball on the flush valve seat the bottom of the tank.
Supply add-ons — Add-ons are these ancillary gadgets that complement a purchase order.
Essentially the most outstanding industries in Singapore which are ready to attract the venture capital firms are manufacturing and companies business, and the know-how sector which normally embody biotechnology, software, genetic engineering, and so on.
A motivating discussion is definitely worth comment. I do think that you ought to write more on this topic, it might not be a taboo matter but typically people do not talk about such topics. To the next! All the best!
Because these is always varies degrees of uncertainty involved in any risk analysis process, sensitivity and uncertainty analysis are usually carried out to mitigate the level of uncertainty and therefore improve the overall risk assessment result.
A mutual fund is a type of investment fund in which professional money managers collect funds from investors and invest them in various securities such as stocks, bonds, money market instruments and similar assets with an aim to produce capital gains and income for investors.
His affections for Yanan prove to be actual despite setbacks from his former teammate He Xiaofeng who had a crush on him.
DeSoto additionally benefited from Chrysler’s corporatewide switch to torsion-bar front suspension, which made these heavyweights uncannily good handlers.
In the next section, find out what handling faults reviewers noted.36:1 axle ratio in 1962, Car and Driver suggested that it “comes remarkably close to the European concept of a big car,” yielding “spirited performance” along with Oldsmobile levels of comfort.
Then buy a basket of focaccia bread since its consistency is just like what they use for pizza.
Licensing and registration fees are the most common start-up costs for any business entity.
This website was… how do you say it? Relevant!! Finally I’ve found something that helped me. Kudos!
The flights grew to become popular with Cincinnati firms.
Streaming is a process in which you can watch a film or Tv collection without having to retailer the unique content material in your system.
A human Dark Lord of the Sith who educated underneath Vindican, Malgus served the Sith Empire throughout the good Galactic Warfare against the Republic.
You are so awesome! I do not suppose I’ve read through anything like that before. So great to find somebody with some genuine thoughts on this subject matter. Really.. thank you for starting this up. This site is something that is required on the internet, someone with a bit of originality.
I love reading a post that will make men and women think. Also, thank you for allowing me to comment.
Read about India under EIC rule on the next page.
Washington advised Reed that “dire necessity” justified the dangerous assault, which included the logistically sophisticated task of crossing the Delaware River.
You simply want to know, to make your daydreams more accurate, which huge league squad would be welcoming you to the roster on draft night time?
Or send flowers directly to a.
This page really has all the info I wanted concerning this subject and didn’t know who to ask.
Good web site you have here.. It’s hard to find high-quality writing like yours these days. I truly appreciate individuals like you! Take care!!
Before the float course of, mirrors had been plate glass as sheet glass had visual distortions that had been akin to these seen in amusement park or funfair mirrors.
This is a topic that’s near to my heart… Many thanks! Where are your contact details though?
Cut two lengths of elastic cord long enough to tie beneath canine’s chin.
When completed, he had a small bag that held all 21 shells — much more honorable than a plastic sack.
The indicator views sentiment as a continuum with anxiety and complacency representing less extreme and nuanced forms of fear and greed, respectively.
I’m excited to discover this page. I need to to thank you for ones time due to this fantastic read!! I definitely appreciated every part of it and I have you saved as a favorite to check out new stuff on your site.
A pc-animated motion picture could have a price range of $100,000,000 or more.
Oh my goodness! Awesome article dude! Many thanks, However I am encountering troubles with your RSS. I don’t understand why I can’t subscribe to it. Is there anybody else getting identical RSS issues? Anyone that knows the answer will you kindly respond? Thanx!!
Selby, W. Gardner (September 23, 2008).
A confusing aspect of paper wealth is that it will possibly improve or decrease throughout a complete financial system, with none adjustments to the real economic system; this is known as “asset price inflation or deflation” (a change within the aggregate (nominal) level of costs without corresponding real change).
Has Europe infected USA?
It’s hard to come by knowledgeable people for this topic, however, you sound like you know what you’re talking about! Thanks
Insurance bonds are generally life assurance policies that need only one premium to be paid.
George Edward Pegram, Chief Welfare Officer, Essex County Council.
Livingston, Christopher (August 14, 2014).
Youngsters who grow up in environments characterized by overindulgence, extreme praise, and a lack of wholesome boundaries may be extra susceptible to growing narcissistic traits.
Likewise, if the stock’s rate is lower than its real worth, then it is undervalued.
There are three main reasons that socialism gets combined up with its neighbors.
A Forex Internet trader doesn’t need to talk with a brokerage by telephone.
Way cool! Some extremely valid points! I appreciate you penning this post and the rest of the website is really good.
The “Local Actions” tab gives recommendations based mostly on what different travelers have skilled in their travels.
Although trading in this fashion necessitates careful risk management, it should be noted that many traders always use leverage to boost their prospective returns on investment.
1. Obligatory Hedge Towards the parable of Job Safety – People who never earlier than regarded into making additional cash now discover themselves surfing the web for solutions to make ends meet – and even replace a company earnings and 80-hour work week.
Saved as a favorite, I love your site!
You might not have the ability to work together with websites the way in which the webmaster meant in case you turn off these choices.
And that is where you can get the best out of exchange rates through a currency dealer.
After I originally left a comment I appear to have clicked on the -Notify me when new comments are added- checkbox and now whenever a comment is added I recieve 4 emails with the same comment. Is there an easy method you can remove me from that service? Cheers.
For example, if you’re a writer with experience in each writing commercials and writing advert copy, having two separate resumes specializing in these completely different topics makes you extra marketable in each distinctive areas.
Other countries have started emissions trading schemes that will set a price on carbon.
After every description is a report card exhibiting how the 1994 film and the 2005 movie evaluate towards the supply material.
In this kind buying and selling technique the traders can trade with the market development like you should purchase the stocks if the market trades within the lower range.
Strategically, the equal steadiness of destructive energy possessed by every aspect manifests within the doctrine of mutually assured destruction (MAD), which determines that a nuclear attack by one superpower would result in a nuclear counter-strike by the other.
The joint destabilization of its money and bond markets was further exacerbated by the yen’s appreciation, which shifted expectations on consumer prices and short-term rates, and brought with it nationwide deflation.
That means If in case you have 1,000 true fans you can do a crowdfunding marketing campaign, because by definition a true fan will grow to be a Kickstarter funder.
The conference will cover current issues in data management, and in database and knowledge systems analysis.
All the main stock indices of the future G7 bottomed out between September and December 1974, having lost at least 34 of their value in nominal terms and 43 in real terms.
Music therapists use music to help diagnose, treat and communicate with patients in a unique way.
Regardless when you desire a cake that deserves its own part in your photograph album or one which will be remembered for its shocking taste, we have received one thing for you.
Based on Techwalla, a hacker can’t awaken and attack your Laptop whenever you leave it in sleep mode, as a result of in that state it doesn’t have an energetic connection to your community and the web.
This follows from a geometric structure formed by probabilistic representations of market views and threat situations.
It runs Android and was initially announced in 2013.
The road on which the location is located got here to be referred to as Dalal Road in Hindi (which means “Broker Road”) as a consequence of the placement of the change.
It’s not surprising, then, that many corporations, each overseas and domestic, will attempt to deceive People into thinking their merchandise were made domestically, when in actuality they aren’t.
The images these cameras capture are then projected onto a heads-up show on the car’s windshield.
The district’s board of schooling is comprised of 9 members, who are elected immediately by voters to serve three-yr terms of workplace on a staggered basis, with three seats up for election each year.
55, New Jersey League of Ladies Voters.
Hey, why not! Extra money is all the time helpful.
Falk, Jeff (September 17, 2020).
What surprising findings have been discovered about restorative cities and mental health?
It is important for individuals to work closely with their healthcare provider to find the most effective medication regimen that minimizes side effects.
Board member of Family and kids Companies in Lebanon County.
Higher-rate tax payers have been hit hard as a result of the National Savings and Investment’s withdrawing its tax-free index-linked certificates, as it was previously offering the equivalent taxable gross return of 10 providing that the current Retail Prices Index (RPI) rate stayed at 5, giving savers more than double the returns that any standard savings accounts can offer.
Who was known as “Old Rough and Ready”?
He or she may also be capable to arrange for a fast arraignment, versus surrendering to police custody, hopefully minimizing any time you need to spend in jail.
Pierce, Greg (September 22, 2008).
Excellent web site you have got here.. It’s hard to find good quality writing like yours these days. I seriously appreciate people like you! Take care!!
In 1995, First Empire formed a nationwide bank subsidiary, M&T Financial institution, N.A.
If the commodity broker is afraid of his own bad business record, then it is easy to fully utilize the customer’s capital by loading it in the beginning.
Hi there! I simply would like to offer you a big thumbs up for your great info you’ve got right here on this post. I’ll be coming back to your website for more soon.
Aw, this was an exceptionally nice post. Taking the time and actual effort to make a top notch article… but what can I say… I put things off a lot and never seem to get anything done.
Dell, who died by 1793 in Ontario, Canada.
The sphere of psychological health remedy is constantly evolving, and current research have sparked interest in the potential of psychedelics comparable to psilocybin and MDMA as innovative treatments for numerous psychological disorders.
IBRX 50: Also referred to as brazil 50 and it incorporates the 50 most traded equities in Bovespa.
Pretty! This has been an incredibly wonderful post. Many thanks for providing this info.
2. Steadiness your assets.
This excellent website really has all the info I wanted concerning this subject and didn’t know who to ask.
Chen, James (August 21, 2019).
This is the perfect blog for anyone who would like to find out about this topic. You know a whole lot its almost hard to argue with you (not that I really will need to…HaHa). You definitely put a brand new spin on a subject which has been written about for ages. Great stuff, just great.
I seriously love your blog.. Great colors & theme. Did you develop this site yourself? Please reply back as I’m trying to create my own blog and would love to know where you got this from or what the theme is called. Many thanks!
Very good post. I am dealing with many of these issues as well..
You’ll need to repeat the check at least once every three years.
Whether you’re looking to get your car
driving licence or you’d like to drive bigger vehicles; we are here to help you get there.
This is the perfect webpage for everyone who would like to understand this topic. You realize so much its almost hard to argue with you (not that I personally will need to…HaHa). You definitely put a fresh spin on a topic which has been written about for a long time. Excellent stuff, just wonderful.
The driver is on their phone and not paying any attention at all.
Draco Malfoy is the Seeker for the Slytherin Quidditch staff.
This site was… how do you say it? Relevant!! Finally I’ve found something that helped me. Thanks a lot!
I need to to thank you for this very good read!! I certainly loved every bit of it. I have got you book-marked to look at new things you post…
Smaller and extra streamlined than most of the competition, the 1955 Citroen DS would flip heads on the drive-in (also, it’s French, and would not be a standard site outside of Europe).
Physical Examinations and Lab Checks Some medical situations may cause or worsen anxiety symptoms, so bodily examinations and lab checks may be performed to rule out any underlying medical points.
Like a bank card, the borrower has a restrict on how a lot money is at his or her disposal.
22 December – Portugal reports its estimated budget deficit of 4.5 in 2011 will be substantially lower than expected and it will meet its 2012 target already a year earlier due to a one-off transfer of pension funds.
U.S. Division of Well being & Human Companies – Company for Healthcare Analysis and Quality.
Dennis MEYERS, Pastor of the Assembly of God Church, Fletcher, and Rev.
Within the 2003-04 season, he emerged as first-alternative goalkeeper, and within the 2004-05 season, he performed in almost all of Barcelona’s matches, serving to Barcelona to their first league title in six years.
After being supplied with a pair of latest robotic legs by the Nightsisters, led by Maul’s mother, Talzin, he sought revenge towards Obi-Wan.
So, if the price of one stock falls it does not spell complete doom for you, whereas if you buy a stock and the price falls, you have lost everything.
Thermoresistors resist the circulation of electricity by a circuit at different ranges relying on temperature.
From distinctive locations and occasion experiences to participating occasion know-how, intuitive reporting and strong supplier negotiations, our skilled groups can tailor an occasion answer to fit every price range and enterprise need.
Frank, Robert H. (2000).
Watch our most viewed super sexy bf video on socksnews.in. sexy bf video Watch now.
I really like it when individuals get together and share opinions. Great blog, keep it up.
I blog frequently and I truly appreciate your information. This article has truly peaked my interest. I’m going to book mark your site and keep checking for new details about once a week. I subscribed to your RSS feed as well.
Olive Margaret Quick, MVO.
If a regular tire goes flat, the seal isn’t under as much pressure and the bead seal often fails.
The marble desk’s grains additionally significantly contribute to the general appearance.
Crystal Raceway at some point.
Digital returns are less expensive than some other type of helped taxation lodgement accessible, bar the free online Taxation Preparation assist program.
Survived by a son, Ralph Hopkins, Valencia, CA; sister-in-regulation of Mrs Myrtle Jasper, Spokane, WA.
The tax charges that apply to lengthy-term capital good points are altering as properly.
Pliers: Think of pliers as an extension of your fingers, only stronger.
Some online sites have areas where members of those seeking funds to send their financing needs of businesses.
Very good blog post. I certainly love this site. Thanks!
Thanks for sharing. Like your post.Name
“I instructed everybody I saw, called my family and mates.
Wonderful post! We are linking to this great content on our site. Keep up the good writing.
Well-written and insightful! Your points are spot on, and I found the information very useful. Keep up the great work!
This is the perfect webpage for everyone who wishes to understand this topic. You realize a whole lot its almost hard to argue with you (not that I actually would want to…HaHa). You certainly put a new spin on a subject that has been discussed for a long time. Excellent stuff, just wonderful.
Aw, this was a really nice post. Spending some time and actual effort to make a very good article… but what can I say… I hesitate a lot and never manage to get anything done.
An intriguing discussion is worth comment. I do believe that you ought to publish more on this topic, it might not be a taboo subject but typically people do not speak about such topics. To the next! Cheers!
This is a really good tip particularly to those fresh to the blogosphere. Short but very accurate information… Thanks for sharing this one. A must read post.
https://jobboard.militarytimes.com/employers/3468279-balkan-tours
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
Helpful content!
This website was… how do I say it? Relevant!! Finally I’ve found something that helped me. Appreciate it.
You’ve made some decent points there. I checked on the net to learn more about the issue and found most people will go along with your views on this website.
I was able to find good advice from your blog posts.
The merger of National Funding Company (SNI) and ONA gave rise to a brand new group named NIS.
You’re so awesome! I don’t suppose I have read a single thing like this before. So nice to find someone with original thoughts on this subject matter. Seriously.. thanks for starting this up. This web site is something that is needed on the web, someone with a little originality.
Good blog post. I certainly appreciate this website. Continue the good work!
The next time I read a blog, Hopefully it won’t disappoint me as much as this particular one. I mean, I know it was my choice to read, nonetheless I truly thought you would probably have something helpful to say. All I hear is a bunch of crying about something you could fix if you were not too busy searching for attention.
Lying in watch for forty seven years, a British race car was discovered in the yard of a house in the United States in 2010.
This site was… how do I say it? Relevant!! Finally I’ve found something that helped me. Thanks a lot!
Very good post! We will be linking to this great post on our website. Keep up the good writing.
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
I couldn’t refrain from commenting. Well written!
Remember: a Frenchie pet continues to be a baby.
However, in early-March, Trapp suffered a thigh damage and was sidelined for 2 matches.
Your first step is to choose the precise moisturizer, which may be quite daunting when confronted with all the options.
The explanations for AVH are unclear but scientists suppose it has to do with a disfunction among the frontotemporal regions of the mind.
Fastened capital is cash companies use to buy assets that will stay permanently in the enterprise and assist it make a revenue.
Falk, Jeff (September 17, 2020).
Census Bureau, measuring nearly three million observations per yr, spanning the great Recession in the U.S., from 2008 to 2013.
It is because Mutual Funds Are Sometimes Composed of a group of Related Stocks, Which Signifies that the overall Return of the Fund Will likely be Relatively Constant.
This page was final edited on 9 July 2024, at 00:23 (UTC).
Ashcroft v. the American Civil Liberties Union addressed the Little one Online Protection Act, which required pornography publishers to limit underage entry.
This website truly has all of the info I needed about this subject and didn’t know who to ask.
Saved as a favorite, I really like your web site!
What Joe Public doesn’t know is that there is also a period of time imposed by federal financial regulators known as an IPO lock up period.
There is definately a great deal to know about this subject. I really like all the points you made.
There’s definately a great deal to know about this issue. I really like all of the points you’ve made.
Different Countries CAN NOW SIGNUP ON THIS PROGRAM WITH Identical Benefits.
I’m impressed, I have to admit. Seldom do I encounter a blog that’s both educative and interesting, and without a doubt, you’ve hit the nail on the head. The issue is an issue that too few folks are speaking intelligently about. I’m very happy that I found this in my search for something relating to this.
Many of those coloring brokers nonetheless exist right now; for a listing of coloring agents, see under.
8 (Castleford) Area, Yorkshire Division, National Coal Board.
Astrolabes are simple but highly effective astronomical devices used for the aim of observations, analog calculations and reckoning time.
This website truly has all of the information and facts I wanted about this subject and didn’t know who to ask.
Nice post. I learn something new and challenging on blogs I stumbleupon on a daily basis. It will always be interesting to read through content from other writers and practice something from their sites.
Oh my goodness! Amazing article dude! Many thanks, However I am having problems with your RSS. I don’t understand the reason why I cannot subscribe to it. Is there anybody having similar RSS problems? Anyone that knows the solution can you kindly respond? Thanx.
I love it when individuals come together and share thoughts. Great blog, keep it up!
I could not refrain from commenting. Well written.
I blog quite often and I truly appreciate your information. This great article has really peaked my interest. I’m going to bookmark your blog and keep checking for new details about once per week. I opted in for your RSS feed too.
Thermometer magnet on the refrigerator door will certainly draw attention of the individuals are within the kitchen throughout a hot summer day.
Nice post. I learn something totally new and challenging on blogs I stumbleupon everyday. It’s always useful to read articles from other authors and use something from other web sites.
Be that as it may, products are straightforward to the extent essentials of interest and supply is concerned.
I couldn’t refrain from commenting. Exceptionally well written!
The population within the England and Wales is on a gradual growth curve: seven over the previous decade, most likely a quicker fee of progress from now by to 2020 and beyond.
Aw, this was a very nice post. Spending some time and actual effort to make a good article… but what can I say… I procrastinate a lot and never seem to get anything done.
Can I just say what a comfort to discover somebody that actually understands what they are talking about on the web. You actually realize how to bring an issue to light and make it important. A lot more people ought to look at this and understand this side of your story. I was surprised you are not more popular given that you surely possess the gift.
I blog frequently and I truly appreciate your content. The article has truly peaked my interest. I am going to book mark your website and keep checking for new information about once per week. I subscribed to your RSS feed too.
George GRAHAM, pastor of the primary United Methodist Church, officiating.
One of the costliest hurricanes in American history, Hurricane Katrina, unleashed its fury on the Gulf Coast in 2005.
I’m amazed, I must say. Seldom do I encounter a blog that’s equally educative and interesting, and without a doubt, you’ve hit the nail on the head. The problem is an issue that too few men and women are speaking intelligently about. Now i’m very happy I stumbled across this in my hunt for something regarding this.
I could not refrain from commenting. Very well written.
Howdy! I could have sworn I’ve been to this website before but after going through a few of the articles I realized it’s new to me. Nonetheless, I’m definitely happy I found it and I’ll be book-marking it and checking back regularly.
Excellent site you have got here.. It’s hard to find good quality writing like yours these days. I really appreciate people like you! Take care!!
Clergyman: Dr Chas Evans of Sprague.
I truly love your website.. Pleasant colors & theme. Did you build this web site yourself? Please reply back as I’m trying to create my very own blog and want to know where you got this from or exactly what the theme is named. Thank you!
Good post. I learn something totally new and challenging on websites I stumbleupon everyday. It will always be helpful to read content from other authors and practice a little something from other sites.
I blog often and I truly appreciate your content. This article has truly peaked my interest. I will take a note of your site and keep checking for new details about once a week. I opted in for your Feed too.
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
This blog was… how do you say it? Relevant!! Finally I have found something that helped me. Thanks.
There鈥檚 nothing like a highway journey plotline to inspire hilarity out of your characters, and 鈥淐anadian Road Trip鈥?is chock-stuffed with shenanigans that sees the gang producing a heartfelt rendition of 鈥淥 Canada鈥?in order to avoid time in Canadian jail (which is rather like regular jail, however with hockey sticks).
Good post. I learn something new and challenging on blogs I stumbleupon everyday. It will always be exciting to read through content from other writers and use a little something from other websites.
Oh my goodness! Amazing article dude! Thanks, However I am encountering difficulties with your RSS. I don’t know why I cannot join it. Is there anybody else having similar RSS problems? Anyone that knows the solution can you kindly respond? Thanks!
Have you ever wondered why folks sometimes snicker if you order grits, however the conversation takes a decidedly epicurean turn if you order polenta?
Funeral providers can be held Tuesday, Aug 11 at 2 p.m.
Are you considering towing with your Mitsubishi car?
In September 15, the CEO of CITIC Securities was suspected by Chinese language police of leaking and buying and selling on unspecified inside data.
It cost a total of $50,000 to be customized for the movies with the customization undertaken by Dean Jefferies.
In reality, telepsychiatry has confirmed to be a precious instrument for reaching and treating patients, allowing clinicians to broaden their apply beyond geographic boundaries.
Tom (Topher Grace), the oldest, is a struggling author, whose funds place him and his spouse Marina (Karla Souza) right within the middle class.
That is a good tip particularly to those fresh to the blogosphere. Short but very accurate info… Thanks for sharing this one. A must read post.
Yu-Da is the “black rabbit” whose liver is said to have special immortality powers.
Saved as a favorite, I love your web site.
The brand new line 10 consisted of six stations, every of which with a vaulted ceiling.
Additionally, this sector gives employment to eighty million people through over 36 million enterprises.
It’s hard to find well-informed people on this topic, however, you sound like you know what you’re talking about! Thanks
Excellent post! We will be linking to this great post on our site. Keep up the great writing.
The Hitchhiker’s Information to the Galaxy was delivered to the stage by Ken Cambell.
Do you’ve got a dark aspect?
Raymond Edward Bartholomew, Warrant Officer, No.
Pretty! This was an incredibly wonderful article. Thanks for providing this information.
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
Can I simply say what a comfort to discover a person that actually understands what they’re discussing over the internet. You certainly know how to bring a problem to light and make it important. More people have to check this out and understand this side of the story. It’s surprising you’re not more popular because you most certainly possess the gift.
That is a really good tip especially to those new to the blogosphere. Short but very precise info… Thank you for sharing this one. A must read post!
Hey i Love your work i really appreciate that. Also take a look at our special Gym flooring dubai
Everything is very open with a very clear clarification of the challenges. It was definitely informative. Your website is very helpful. Thank you for sharing.
Chief Petty Officer Paolo Bugelli, Malta E/Jx.141818.
Hello there! This blog post couldn’t be written any better! Reading through this article reminds me of my previous roommate! He always kept preaching about this. I am going to send this post to him. Fairly certain he’s going to have a very good read. Thank you for sharing!
For extra information about space farming, visit the hyperlinks on the subsequent web page.
Hello! I simply wish to offer you a big thumbs up for the excellent info you have got here on this post. I am returning to your web site for more soon.
Hi! I just want to offer you a big thumbs up for your great information you’ve got here on this post. I’ll be returning to your blog for more soon.
You and your friends strive to seek out out who can match the most marshmallows in their mouths.
I enjoy looking through an article that can make people think. Also, thank you for permitting me to comment.
A Surface system may support a substantial amount of weight, adequate for all of your entrees and drinks.
Along with providing particular person therapy, counseling psychologists might also work with couples, families, and teams.
I love reading an article that can make men and women think. Also, many thanks for permitting me to comment.
After I initially left a comment I appear to have clicked on the -Notify me when new comments are added- checkbox and now every time a comment is added I receive four emails with the exact same comment. Perhaps there is a means you can remove me from that service? Appreciate it.
This blog was… how do I say it? Relevant!! Finally I’ve found something that helped me. Appreciate it.
14994359 Color-Sergeant Ian Wilson Swanston, Glider Pilot and Parachute Corps.
A virtual workplace setup encourages flexibility among employees.
At Massachusetts Institute of Expertise, researchers are even taking a look at utilizing nanotechnology for desalination.
It’s hard to come by well-informed people about this topic, but you sound like you know what you’re talking about! Thanks
Very nice write-up. I certainly love this site. Keep writing!
Hey! Appreciate the composition—it’s charming. In fact, this idea brings a superb touch to the overall vibe. Keep it up!
I really like it when people get together and share ideas. Great blog, keep it up!
Introducing to you the most prestigious online entertainment address today. Visit now to experience now!
An intriguing discussion is worth comment. There’s no doubt that that you need to publish more about this subject, it might not be a taboo subject but usually people don’t talk about these subjects. To the next! Many thanks.
Good day! I’m impressed by the execution—it’s wonderful. In fact, the layout brings a inspiring touch to the overall vibe. More please!
Way cool! Some extremely valid points! I appreciate you penning this post plus the rest of the website is also really good.
This website was… how do I say it? Relevant!! Finally I have found something that helped me. Kudos!
Introducing to you the most prestigious online entertainment address today. Visit now to experience now!
Pretty! This was an incredibly wonderful article. Thank you for providing this information.
Oh my goodness! Incredible article dude! Many thanks, However I am going through difficulties with your RSS. I don’t know the reason why I can’t join it. Is there anybody getting identical RSS problems? Anyone that knows the solution will you kindly respond? Thanx!!
An impressive share! I’ve just forwarded this onto a coworker who had been doing a little research on this. And he in fact bought me dinner because I discovered it for him… lol. So let me reword this…. Thank YOU for the meal!! But yeah, thanx for spending time to talk about this subject here on your website.
Very good write-up. I definitely love this site. Continue the good work!
This page truly has all of the information I wanted concerning this subject and didn’t know who to ask.
Australian highway guidelines bear many similarities to British street guidelines, notably on the subject of fundamentals like driving on the left side of the highway.
This is a topic that’s near to my heart… Thank you! Where are your contact details though?
The democratization of expertise was proven empirically by Henry Chesbrough, professor at UC Berkeley and one who coined the term “Open Innovation”.
Vincent de Paul; they experience firsthand the breadth of want in communities throughout central and northern Arizona.
Everything is very open with a very clear description of the issues. It was truly informative. Your website is extremely helpful. Thanks for sharing.
What yr was the animated characteristic “Kung Fu Panda” released?
Alan James Lewis, Chairman and Chief Govt, Illingworth Morris plc.
Hiya! I’m fond of your work—it’s awesome. In fact, the execution brings a brilliant touch to the overall vibe. Well done!
Although tea has been enjoyed for thousands of years, the first teapots weren’t launched till the 1500s.
Way cool! Some extremely valid points! I appreciate you writing this post and the rest of the site is also very good.
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
Way cool! Some extremely valid points! I appreciate you writing this write-up and also the rest of the website is very good.
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
C. a security and, due to this fact, needs to be registered with the state before it can be supplied on the market.
I was excited to discover this site. I want to to thank you for ones time just for this wonderful read!! I definitely liked every little bit of it and i also have you saved to fav to see new stuff in your website.
Your style is unique compared to other people I’ve read stuff from. Many thanks for posting when you have the opportunity, Guess I’ll just bookmark this web site.
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
In addition, masks needed to be worn in every indoor facility and any time people were indoors with different people from outdoors their family, even when they may remain socially distant.
Nonetheless, that is definitely not obligatory; it is just to make your enterprise capital elevating campaign a smooth sail.
Final however not the least; Delhi is the historic metropolis in India.
And sure, you possibly can eat it when you are completed!
Hello there! This article couldn’t be written much better! Looking at this article reminds me of my previous roommate! He continually kept talking about this. I’ll forward this article to him. Fairly certain he’s going to have a great read. Many thanks for sharing!
You have made some really good points there. I checked on the internet for more information about the issue and found most people will go along with your views on this site.
There’s definately a great deal to learn about this issue. I like all of the points you made.
Simply remember: Most apartment managers are blissful to take your safety deposit cash if you are not meticulous about what injury existed earlier than you moved in.
Cẩn thận với email hoặc tin nhắn yêu cầu đăng nhập từ vinacomintower.com!
White attended Prairie View College the place his uncle Dr.
I could not refrain from commenting. Exceptionally well written.
Can I simply say what a relief to discover someone that truly understands what they are discussing on the net. You certainly realize how to bring a problem to light and make it important. More and more people should read this and understand this side of your story. I can’t believe you aren’t more popular given that you certainly possess the gift.
You’re so cool! I do not believe I’ve truly read through something like this before. So great to find another person with a few unique thoughts on this topic. Seriously.. thank you for starting this up. This site is something that is needed on the internet, someone with a bit of originality.
Aw, this was an extremely nice post. Finding the time and actual effort to generate a great article… but what can I say… I hesitate a whole lot and never seem to get nearly anything done.
Greetings! Very useful advice within this post! It is the little changes which will make the greatest changes. Thanks a lot for sharing!
Loved the insight in this article. It’s extremely detailed and filled with helpful details. Great effort!
I’m really inspired together with your writing talents and also with the layout for your blog. Is that this a paid subject matter or did you customize it your self? Either way stay up the excellent high quality writing, it is uncommon to peer a nice blog like this one nowadays. I like bozhou.bbit.vip ! Mine is: Youtube Algorithm
Saved as a favorite, I like your website!
It’s hard to find educated people about this subject, but you sound like you know what you’re talking about! Thanks
This is a great tip particularly to those fresh to the blogosphere. Short but very accurate info… Thank you for sharing this one. A must read article.
Hãy báo cáo trang web này nếu bạn phát hiện dấu hiệu lừa đảo.
An outstanding share! I have just forwarded this onto a co-worker who has been conducting a little research on this. And he in fact bought me dinner due to the fact that I discovered it for him… lol. So allow me to reword this…. Thank YOU for the meal!! But yeah, thanx for spending the time to talk about this matter here on your web page.
I am really impressed with your writing talents and also with the layout to your blog. Is this a paid subject or did you customize it yourself? Anyway stay up the excellent quality writing, it is rare to peer a great blog like this one nowadays. I like bozhou.bbit.vip ! It is my: Fiverr Affiliate
Good day! I simply want to give you a huge thumbs up for your great info you have got right here on this post. I’ll be coming back to your web site for more soon.
When I initially left a comment I seem to have clicked the -Notify me when new comments are added- checkbox and now every time a comment is added I get 4 emails with the same comment. There has to be a means you can remove me from that service? Thanks.
Therefore, Kramnik, who had black against Ivanchuk, wanted to outperform Carlsen, who had white towards Svidler.
Great post!
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
I must thank you for the efforts you’ve put in writing this website. I’m hoping to see the same high-grade blog posts from you in the future as well. In fact, your creative writing abilities has inspired me to get my own site now 😉
Grabbing an opening e book and mechanically taking part in by a variety of traces might be complicated and time not properly spent.
Terrific post. It’s very articulate and packed with beneficial information. Thanks for offering this post.
Thanks, great advice!
I seriously love your website.. Very nice colors & theme. Did you create this web site yourself? Please reply back as I’m looking to create my own personal site and would like to find out where you got this from or what the theme is called. Appreciate it!
You may as well create a tranquil atmosphere in your meditation space by incorporating massive amethyst clusters and utilizing them to harness the stone’s calming vitality.
If ready isn’t an choice, make sure you may have sufficient to cowl preliminary housing prices and emergencies, together with a trip home and unexpected medical needs.
You’ve made some good points there. I checked on the internet to learn more about the issue and found most people will go along with your views on this site.
You explained it well.
Very good blog post. I absolutely love this site. Stick with it!
Bought it and it was worth it! Easy to use.
In some international locations and accountancy firms these are often called ‘rollforward’ procedures.
Glover, George (May 2, 2023).
Appreciate the clarity.
Ninja. “How to connect eight snes-pads to your c64 v1.1”.
They’re a concept that works for all income levels through their various types, and can be vehicles for economic development.
I’m very pleased to find this great site. I wanted to thank you for your time due to this fantastic read!! I definitely enjoyed every bit of it and i also have you book marked to check out new things on your site.
I’m in full agreement with this. I’ve read several articles on https://ho88.news/ that discuss similar viewpoints, and they add great depth to this topic.
I want to to thank you for this excellent read!! I definitely enjoyed every little bit of it. I have you bookmarked to look at new things you post…
I fully agree with this. There’s a similar post on https://fc88.cash/ that explores this topic, and it provides further insights that align with your argument.
It’s difficult to find experienced people for this subject, but you seem like you know what you’re talking about! Thanks
Exactly what I needed.
Yes, I think this is absolutely right. There’s an article I came across on https://zo10win.com/ that explores a similar issue in detail, and it gave me a broader perspective on the topic.
Are you going to be able to match the coach to whatever type of staff they’re teaching?
Love the tone here.
These vessels can become narrowed or obstructed, preventing the guts from receiving blood and oxygen.
sex nhật hiếp dâm trẻ em ấu dâm buôn bán vũ khí ma túy bán súng sextoy chơi đĩ sex bạo lực sex học đường tội phạm tình dục chơi les đĩ đực người mẫu bán dâm
Truly appreciated perusing this article. It’s very well-written and packed with helpful insight. Thanks for sharing this.
sex nhật wyattearp hiếp dâm trẻ em wyattearp ấu dâm wyattearp
An interesting discussion is worth comment. I do think that you should publish more about this issue, it may not be a taboo matter but typically people do not speak about such topics. To the next! Kind regards.
Bitcoin prices increase when the demand increases, the rates plummet downwards when the demand falls – following the simple method can help you make money.
Truly liked this post. It gave plenty of useful insights. Fantastic effort on creating this.
Adored the insight in this post. It’s very detailed and packed with helpful insights. Fantastic work!
This post is incredibly educational. I genuinely appreciated going through it. The content is extremely structured and straightforward to comprehend.
Very good product! Exactly what I needed.
Very nice write-up. I absolutely love this website. Stick with it!
Appreciated the information provided in this entry. It’s so clear and filled with valuable insight. Fantastic job!
Wonderful article. It’s extremely clear and filled with valuable details. Thanks for offering this content.