DARTS: DIFFERENTIABLE ARCHITECTURE SEARCH
摘要
本文通过以可微分的方式解决架构搜索的可扩展性挑战。 与在离散和不可微搜索空间上应用进化算法或强化学习的传统方法不同，作者的方法是基于架构表示的连续松弛，能够使用梯度下降对架构进行有效搜索。 在 CIFAR-10、ImageNet、Penn Treebank 和 WikiText-2 上进行的大量实验表明，该算法在发现用于图像分类的高性能卷积架构和用于语言建模的循环架构方面表现出色，同时比现有的不可微分方法快几个数量级。下面，简单介绍下Darts对网络架构搜索的建模以及具体的松弛方法。
搜索空间
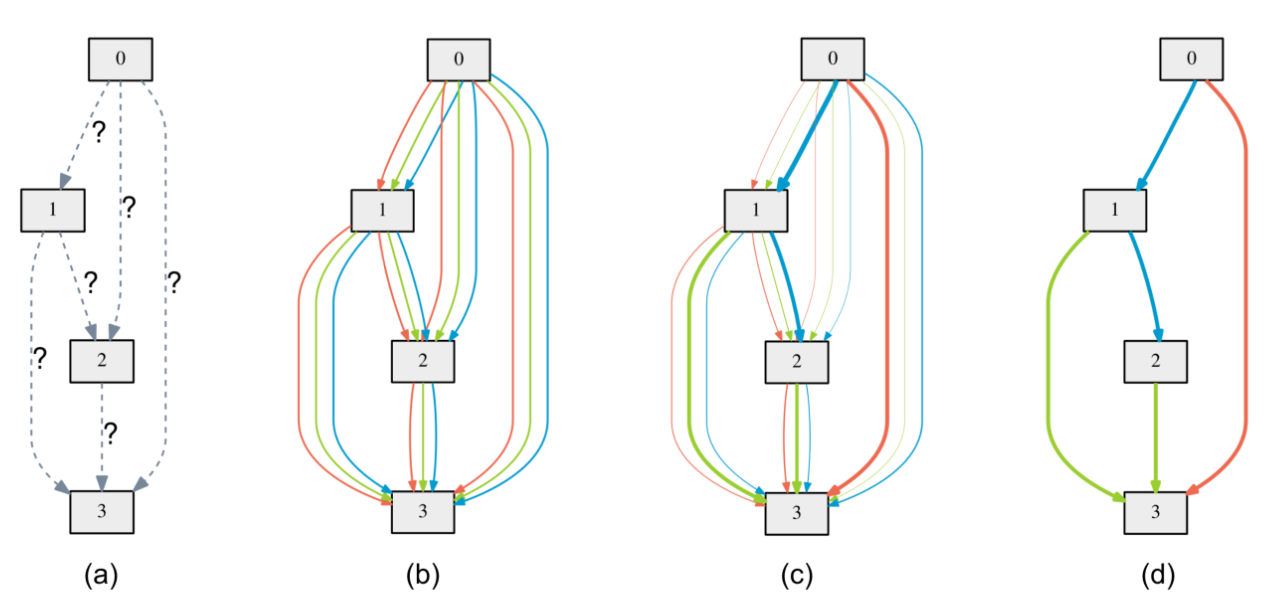
搜索空间被建模成如图所示的超网络。图中的方块表示的是featuremap，有向边表示连接两个featuremap的所有可能操作，且每条边只对应一个操作。(a) 边上的操作最初是未知的。(b) 通过在每条边上放置候选混合操作建立搜索空间。(c) 通过求解双层优化问题联合优化混合概率和网络权重。(d) 从学习到的混合概率中归纳最终架构。注意这里说的混合跟集成学习或者是注意力的意思有点像。也就是在超网络的训练中，两个featuremap之间的所有操作都是要参与到前向传播的，不同操作输出的featuremap被加权求和后作为新的featuremap。
Darts的重点是每个候选操作的权重如何构建，以及如何松弛。
松弛方法
\bar{o}^{(i, j)}(x)=\sum_{o \in \mathcal{O}} \frac{\exp \left(\alpha_o^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)} o(x) 将上图中的有向边对应到操作的表示符号 o(x)，每个操作的权重则是
\frac{\exp \left(\alpha_o^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)}.其中，\alpha 是可训练的参数。如此，该权重具有以下特点：
- 可微分，权重具有自适应能力。
- 和为1，确保输出的featuremap在正常范围内。
- 权重越大，相应的候选操作在输出的featuremap中的贡献越大。
基于上述特点，在训练完成后，选择权重最大的候选即可。
训练算法
在训练的过程中，架构参数与模型参数被视作两组独立的参数交替使用梯度下降进行优化。参数收敛后，根据架构参数的最大值确定每两个featuremap之间的操作，从而生成最终架构。