Deep Residual Learning for Image Recognition
简介
深层次的神经网络很难训练。何恺明等人为了解决这一问题，提出了一个残差学习框架，以简化比以前使用的网络更深的网络的训练。作者明确地将网络层的目标定义为学习该网络层的输入的残差函数。作者提供了全面的经验证据，表明这些残差网络更容易优化，并且可以从显着增加的深度中获得准确性。在 ImageNet 数据集上，评估了深度高达 152 层的残差网络——比 VGG 网络深 8 倍，但复杂度仍然较低。这些残差网络的集合在 ImageNet 测试集上达到了 3.57% 的错误率，该结果在 ILSVRC 2015 分类任务中获得第一名。
方法
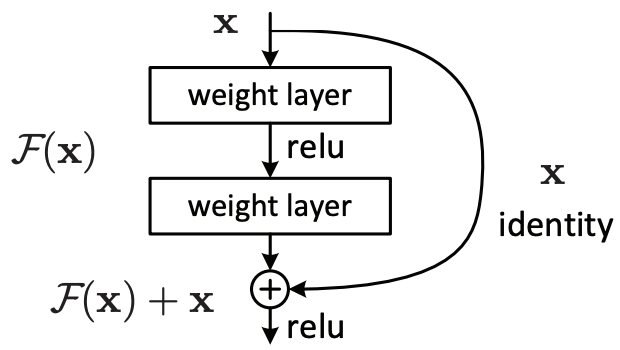
在ResNet中，一个基本的网络块如图所示。其中的每个weight layer都是一个卷积层，这个块包含了一个单独的输入，以及处理该输入的两条路径，左边的路径包含两个卷积层，记作 F(x)，右边的路径不做处理，记作 x，最后输出时，将两条路径的计算结果进行加和。
Residual的优势
ResNet有啥好处？首先，因为 x 被直接引入到输出结果中，那么前面的网络层收到的梯度肯定是会变大了，这就给优化深层次的网络带来了机会。其次，我们考虑这里 x 已经是一个很接近目标值的特征了，但是还是有一定的误差存在，这时候就可以使用 F(x) 来弥补这个误差了，预测 x 和目标之间的误差相比于直接预测目标，是一个更加简单的问题。比如 x 已经很接近目标了，不妨假设一些项已经和目标是完全一致的了，这就相当于降低了F(x)的预测目标的复杂度，而且，x 与目标越相似，F(x)的预测目标的复杂度就越低，那么交给 F(x) 的任务就越简单。直观上去理解这件事情，就好像是，我们先用个模型去拟合这个目标，然后再搞一个模型去消除这个误差，而且新加的这个模型是依据原来的模型提取出来的更加简单的特征进行学习的。本来已经能够预测正确的样本对于 F(x) 而言都属于同一个类别，因为相应的目标就是 0，F(x) 需要做的就是在剩下的还没有预测正确的样本中，通过消除一部分误差，再预测正确一些。显然，这样能够实现更好的性能。
存在的问题
使用上面所示的残差块有一定的限制条件：要求输入的图片的channel、size和输出的图片的channel、size完全一致，要不然怎么加一起呢？在原论文中，作者针对输入和输出的size不一致的情况提出在右边的路径上使用一个简单的卷积对 x 的size进行调整，从而与左边路径上的输出size保持一致。
显然，这个优化使得residual失去了原本的价值。我们按照刚才分析的 F(x) 的作用，再看看他在这个场景下作用是啥。现在左边的路径还是 F(x)，右边的路径是 G(x) -- 一个一层的卷积网络。刚才咱们提到，x 如果已经很接近目标的话，那么对于 F(x) 而言，有相当大的一部分样本的标签就直接是 0 了，因为F(x)是要预测x和目标之间的残差，这大大简化了F(x)的输入和输出之间的关系，F(x)可以明确的知道自己要干嘛了。可是，右边路径换成G(x)，F(x)要预测的目标变成了 y-G(x)，而G(x)有自己的参数，会变化！F(x)想知道，自己到底是在预测个啥。这个时候还按照残差的思路去考虑这个模型已经说不通了。当右边的路径被换成G(x)，这更像是一个模型的集成！F(x)是两层，G(x)是一层，F(x)的性能只会被G(x)拖累，因此不能产生很好的优化效果！
那这种输入和输出的size不一致的情况咋处理？我的建议是不处理，也就是不使用residual连接。论文里提出的residual真正发挥作用的时候，应该是为一个本来就不错的模型拟合一下他的残差，从而进一步提升这个模型的性能。考虑一个极端的情况，从一开始就使用residual，每个卷积层都用，那会发生什么？就是最一开始的特征 x 直接被传到了最后用于类别的预测，这就相当于用了一个0层的神经网络来学习某个分布，然后用了一个几十层的神经网络来学习这个0层的神经网络的残差！我们前面就假设 x 已经是一个很接近目标的特征了，这就需要在使用residual技巧之前就已经对特征进行了充分的提取，这样才能更好的发挥residual的作用。鉴于此，输入和输出的size不一致的情况索性不处理，直接当成普通的卷积层进行前向传播，这事实上恰好可以帮助我们提取更好的特征 x。