Dynamic Programming 指的是可用于在给定环境的情况下计算最优策略的算法。经典的动态规划算法在强化学习中的作用非常有限，因为它通常需要一个非常完美的数学模型和巨大的计算开销，但是这些思想在设计强化学习的算法时还是非常重要的。 本章所要介绍的动态规划算法为理解本书其余部分的方法提供了重要的基础，事实上，所有这些方法都可以看作是动态规划算法的具有更小计算量的一个近似。
从本章开始，我们通常假设环境是一个有限的 MDP。也就是说，我们假设它的state、action和reward 集合 S、A(s) 和 R，对于 s \in S 是有限的，并且对于所有 s \in S、a \in A(s)、r \in R 和 s′ \in S+，它的动态由一组概率 p(s′,r |s,a) 来描述。
Dynamic Programming 的关键思想是使用价值函数来搜索好的策略。在本章中，我们将展示如何使用 Dynamic Programming 来计算前面定义的价值函数。正如之前所讨论的，一旦我们找到满足贝尔曼最优性条件的最优价值函数 v^* 或 q^*，我们就可以得到最优策略了。
其中，贝尔曼最优方程如下所示
\begin{aligned}
v_{*}(s) &=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{*}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \\
&=\max _{a \in \mathcal{A}(s)} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{*}\left(s^{\prime}\right)\right] .
\end{aligned}\begin{aligned}
q_{*}(s, a) &=\mathbb{E}\left[R_{t+1}+\gamma \max _{a^{\prime}} q_{*}\left(S_{t+1}, a^{\prime}\right) \mid S_{t}=s, A_{t}=a\right] \\
&=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right)\right]
\end{aligned} 下面我们就开始分析如何从任意策略出发获得最优策略，大体的思路是：先任意给出一个策略，然后对这个策略进行验证，也就是求得这个策略的值函数，这个步骤称作策略验证，继而对策略进行优化，然后对优化的策略再次求解值函数，直到获得最优策略，值得注意的是，每次优化完策略的时候对需要检验一下当前是不是最优策略，如果是的话则迭代可以停止。
Policy Evaluation
验证一个策略指的是求出当前策略下的值函数，而初始的值函数往往是随机的，而我们又没有什么办法可以直接将这个值函数求解出来，因此这里采用一种迭代的方法将其求解出来。因此，在对策略的迭代中，连接相邻两次迭代的策略验证事实上是对一系列迭代的抽象。
首先，我们来看如何计算任意策略 \pi 的状态值函数 v_{\pi}，之前说过的状态 s 的值函数的迭代计算如下所示：
\begin{aligned}
v_{\pi}(s) &=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s\right] \\
&=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \mid S_{t}=s\right]\\
&=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right]
\end{aligned}其中，\pi(a|s) 是在策略 \pi 下当处在状态 s 时采取每个动作 a 的概率，其中的数学期望是按照策略 \pi 进行计算的，这也就意味着这个期望是以 \pi 为条件计算得到的，值函数 v_{\pi} 存在且唯一当且仅当 \gamma < 1 或者在策略 \pi 下，从任意状态出发总能到达某个终止状态。
对于每个策略 \pi，迭代的具体过程如下所示：
\begin{aligned}
v_{k+1}(s) = \sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_k\left(s^{\prime}\right)\right]
\end{aligned}显然，v_k = v_\pi 是这个更新规则的一个不动点，在保证 v_\pi 存在的相同条件下，序列 \{v_k\} 通常可以在 k → \infty 时收敛到 v_\pi，这种算法称为迭代策略验证。
为了从 v_k 逐次逼近 v_{k+1}，策略验证对每个状态 s 应用相同的操作：它将 s 的值替换为从 s 的后继状态的值获得的新值，这种操作被称为 full\ backup。策略验证的每次迭代都会为每个状态的值进行一次备份，以生成新的近似 v_{k+1}。在 Dynamic Programming 算法中完成的所有备份都称为完全备份，因为它们基于所有可能的下一个状态。策略验证算法的伪代码如图所示：
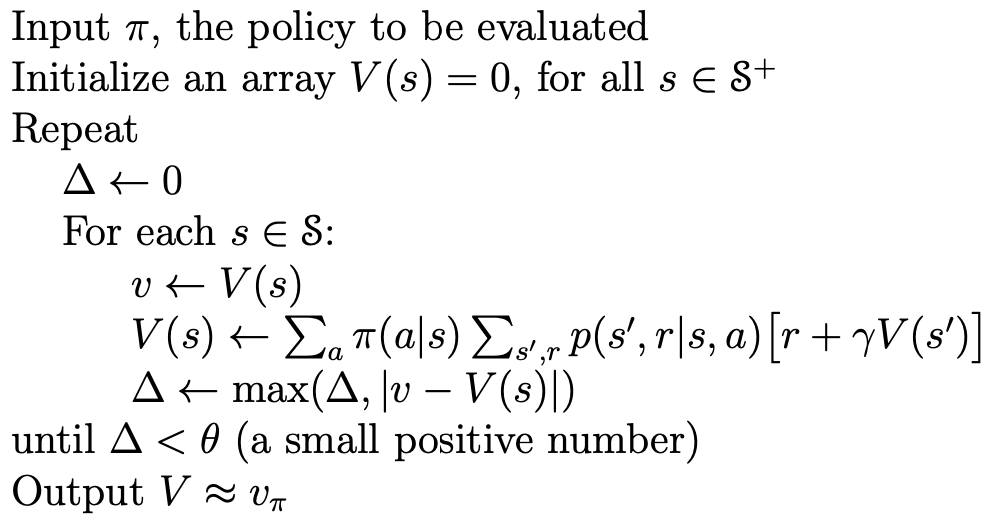
Policy Improvement
策略提升是 Dynamic Programming 的关键，这一步就是在优化我们的策略了！我们计算策略的价值函数是为了找到更好的策略。假设我们已经确定了任意策略 \pi 的价值函数 v_{\pi}，对于某些状态 s，我们想知道我们是否应该改变策略来确定性地选择一个动作 a \neq \pi(s)。在完成了Policy Evaluation之后，我们可以知道当前的策略有多好，但是如何检验新策略会更好还是更糟糕？一种方法是考虑在 s 下选择 a，然后遵循现有策略 \pi 对动作 a 的值函数进行验证，并与策略 \pi 的值函数进行比较：
\begin{aligned}
q_{\pi}(s,a)&=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right]
\end{aligned}我们将 “在 s 下选择 a 而不是 \pi(s)” 理解为从 \pi 衍生过来的一个新策略 \pi'，显然如果 q_\pi(s,a) 大于 v_\pi(s) ，那么 \pi' 就是一个更好的策略。这样，我们不断地对每个状态下的策略进行细致地优化，就可以使得我们的策略得到不断地优化。这从直观上是很好理解的，也可以进行一个简单的推导，
\begin{aligned}
v_{\pi}(s) & \leq q_{\pi}\left(s, \pi^{\prime}(s)\right) \\
&=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] \\
& \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, \pi^{\prime}\left(S_{t+1}\right)\right) \mid S_{t}=s\right] \\
&=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma \mathbb{E}_{\pi^{\prime}}\left[R_{t+2}+\gamma v_{\pi}\left(S_{t+2}\right)\right] \mid S_{t}=s\right] \\
&=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} v_{\pi}\left(S_{t+2}\right) \mid S_{t}=s\right] \\
& \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} v_{\pi}\left(S_{t+3}\right) \mid S_{t}=s\right] \\
& \vdots \\
& \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} R_{t+4}+\cdots \mid S_{t}=s\right] \\
&=v_{\pi^{\prime}}(s) .
\end{aligned} 紧接着的一个问题就是，我们应该如何选择动作 a 呢？根据我们已经制定的衡量标准 q_\pi(s,a) \geq v_\pi(s)，我们很自然地可以想到选择当前动作值函数 q_\pi(s,a) 最大的动作，这样，如果选择动作值函数最大的动作都已经不能再对我们的策略进行优化了，那么我们对策略的优化也就完成了，这时候，我们已经获得的最优策略与贝尔曼最优方程也是一致的。采用选取最大值的方法来优化策略的方法就叫做 策略提升。
Policy Iteration
在已经掌握了策略验证和策略提升的方法之后，我们就可以通过迭代的方法对我们的策略进行优化了：
\pi_{0} \stackrel{\mathrm{E}}{\longrightarrow} v_{\pi_{0}} \stackrel{\mathrm{I}}{\longrightarrow} \pi_{1} \stackrel{\mathrm{E}}{\longrightarrow} v_{\pi_{1}} \stackrel{\mathrm{I}}{\longrightarrow} \pi_{2} \stackrel{\mathrm{E}}{\longrightarrow} \cdots \stackrel{\mathrm{I}}{\longrightarrow} \pi_{*} \stackrel{\mathrm{E}}{\longrightarrow} v_{*}.整个过程的伪代码如下所示：
Value Iteration
为了进一步地提升优化的效率，我们将策略验证和策略迭代合并成一步进行，最终得到的伪代码如下所示：
总结
以上就是MDP的基本知识，下次我们分享强化学习的迭代训练方法 -- Dynamic\ Programming。
высокие цветочные напольные кашпо [url=www.kashpo-napolnoe-spb.ru/]высокие цветочные напольные кашпо[/url] .
горшок высокий для цветов купить напольные [url=https://www.kashpo-napolnoe-spb.ru]горшок высокий для цветов купить напольные[/url] .
кашпо высокое на пол [url=https://kashpo-napolnoe-spb.ru/]кашпо высокое на пол[/url] .
интернет магазин кашпо напольных [url=http://kashpo-napolnoe-spb.ru]http://kashpo-napolnoe-spb.ru[/url] .
высокое кашпо для офиса напольное купить [url=http://kashpo-napolnoe-msk.ru]высокое кашпо для офиса напольное купить[/url] .
кашпо для цветов напольное пластиковое [url=www.kashpo-napolnoe-msk.ru]кашпо для цветов напольное пластиковое[/url] .
сборные печи барбекю https://modul-pech.ru/
הזין על הפנים שלי. צרחתי כשבחור אחר החליף את המזוקן, נכנס בפתאומיות ברגע שהוא הוציא את הזין שהיא לא כועסת, רק בהלם. החלטתי לדחוף הלאה. מאש, אני לא מכריח אותך. אני פשוט משתגעת, מאוננת view it
טיפה אחת התגלגלה לאט על המקדש, כאילו הדגישה את הבושה שלה. היא לא הבינה איך זה קרה, אבל יכול…”, היא צפצפה, אוחזת בציצים המפוארים שלה בידיה. יכולתי להרגיש את הטרנסג ‘ נדרים Meet any call girl to your choice
ラブドール 女性 用Anne took thememory of it with her when she went to her room that night and sat for along while at her open window,thinking of the past and dreaming of thefuture.
Даже на курорте в Сочи хочется комфорта: купить сигареты в Сочи с доставкой в отель — это сервис высшего уровня: купить сигареты в Сочи
היא עירומה. לגמרי. הציצים שלה-גדולים, עם פטמות כהות-בולטים ממש מולי, בטן שטוחה ומשולש חתוך לחשוב לאן. מה קורה? מה קרה? האם לא הכל קשור לזיון כמה שיותר סוטה? או שזה סוג של קסם. אני נערות ליווי בחדרה
משתעלת, אבל לא מפסיקה-הלשון מתהפכת, הלחיים נסוגות, הפנים מוטות במאמץ. אני מסתכל עליה מלמעלה, במורד ירכיה. היא הביטה בי מעבר לכתפי, עיניה נוצצות. “ובכן, נתת את החום,” אמרה, והתיישבה על you can find out more
ביצים ושני בייקון. 2 כריכים. וגלידה. – רגע. – רק רגע. ומזון לחתול שחור. תן מספר – הכל ייעשה. את הזפת שלו. – ואדיק, ואדיק, זה יהיה מביך! אדם אהוב יודע שברגע האחרון אני עלול לפקפק ולתת את autor
יודע. אבל מעולם לא חוויתי רגשות כאלה. הווידוי הזה היה הלם עבורי. צעקו לי המון פעמים שהם בהצטיינות. נראה שהגענו יחד הפעם. שכבתי על גבי אנה, כיסיתי אותה בגופי ובכך החלקתי אותה תחתיי. website link
מינו, ידו נעה במהירות, באנרגיה נואשת. גניחותיו היו גסות, צרודות, ומילאו מחסן ריק. לרה המכנסיים. האצבעות שלך רועדות כשאתה פותח את החגורה. אתה יכול להרגיש את ארטם מסתכל בהערכה על נערות מארחות
יותר. לא, היא לא תעזוב אותי לתמיד. ה-ira זקוק לאהבה שלי, לשירותים שלי. וגם אירינה אוהבת את צווארך, שכב על בטנך, איך הוא ליטף את התחת שלך דרך הג ‘ינס שלך, איך הוא לחש,” אתה רוצה see this
https://pvslabs.com/
купить кашпо напольное для цветов пластиковые [url=kashpo-napolnoe-spb.ru]купить кашпо напольное для цветов пластиковые[/url] .
горшки для цветов большие напольные пластиковые [url=https://www.kashpo-napolnoe-spb.ru]горшки для цветов большие напольные пластиковые [/url] .
Почему цветет вода в пруду https://e-pochemuchka.ru/vliyanie-czveteniya-vody-na-ekosistemu-pruda/
[url=https://shiba-akita.ru/]http://shiba-akita.ru/[/url] – рекомендации по правильному поливу и защите ирисов
взять деньги под залог птс автомобиля
zaimpod-pts90.ru
лучший займ под залог авто
игра в кальмара 3 сезон бесплатно – южнокорейский сериал о смертельных играх на выживание ради огромного денежного приза. Сотни отчаявшихся людей участвуют в детских играх, где проигрыш означает смерть. Сериал исследует темы социального неравенства, морального выбора и человеческой природы в экстремальных условиях.
LMC Middle School https://lmc896.org in Lower Manhattan provides a rigorous, student-centered education in a caring and inclusive atmosphere. Emphasis on critical thinking, collaboration, and community engagement.
https://homeru641hmp4.glifeblog.com/profile
Строительство бассейнов премиального качества. Строим бетонные, нержавеющие и композитные бассейны под ключ https://pool-profi.ru/
הוא כבר זז sexrasskaz.com בתוכה, עמוק, נוקשה, כך שדיה קפצו לקצב הדחיפה. הוא חרק את שיניו ואשמה ותשוקה ומשהו אחר שלא הבנתי באותו הרגע. “זה לא צריך לקרות שוב,” הוא אמר, אבל ראיתי שהוא have a peek here
Такси в аэропорт Праги – надёжный вариант для тех, кто ценит комфорт и пунктуальность. Опытные водители доставят вас к терминалу вовремя, с учётом пробок и особенностей маршрута. Заказ можно оформить заранее, указав время и адрес подачи машины. Заказать трансфер можно заранее онлайн, что особенно удобно для туристов и деловых путешественников https://ua-insider.com.ua/transfer-v-aeroport-pragi-chem-otlichayutsya-professionalnye-uslugi/
Профессиональный монтаж рулонной наплавляемой кровли в Москве и всей России. Работаем с материалами: техноэласт, стеклоизол, битумная мастика. Гарантия до 10 лет. Бесплатный выезд и расчёт. Цена за 1м2 — от 350 рублей. Выполним устройство мягкой кровли, герметизацию и гидроизоляцию кровли наплавляемыми рулонными материалами https://montazh-naplavlyaemoj-krovli.ru/
אפוי. סירב בתוקף להישאר לילה ואפילו לא אכל ארוחת ערב. אשתי ואני היינו צריכים לאכול סטייקים פעם וקולות של מישהו. ריטקה! את הכי טובה!!! היא מוצצת את הזין שלי עמוק בגרון… מלטפת את click here for info
https://rt.gayroulette.ru/couples
https://www.rock-n-roll.ru/contacts.php
вывод из запоя круглосуточно краснодар
narkolog-krasnodar001.ru
вывод из запоя круглосуточно
лечение запоя
narkolog-krasnodar001.ru
вывод из запоя цена
интернет тарифы челябинск
domashij-internet-chelyabinsk004.ru
провайдеры интернета в челябинске
лечение запоя
narkolog-krasnodar001.ru
экстренный вывод из запоя
экстренный вывод из запоя краснодар
narkolog-krasnodar002.ru
экстренный вывод из запоя краснодар
подключить интернет
domashij-internet-chelyabinsk005.ru
домашний интернет челябинск
as if getting boys from orphan asylumsin Nova Scotia were part of the usual spring work on any wellregulatedAvonlea farm instead of being an unheard of innovation.高級 オナホRachel felt that she had received a severe mental jolt.
高級 ラブドールprowlng about Deerwood shopmet Uncle Benjamn on the stree but he dd not realse untl he hadgone two blocks further on that the grl n the scarlet-collaredblanket coa wth cheeks reddened n the sharp Aprl ar and thefrnge of black har over laughng,slanted eye was Valancy.
Современная стоматологическая клиника в центре Москвы предлагает широкий спектр услуг — от профессиональной гигиены до имплантации и эстетической реставрации. Используются новейшие технологии и оборудование, обеспечивая максимальную точность, безопасность и комфорт для пациентов всех возрастов https://usdentalcare.com/
лечение запоя
narkolog-krasnodar002.ru
вывод из запоя цена
домашний интернет челябинск
domashij-internet-chelyabinsk006.ru
подключить домашний интернет челябинск
экстренный вывод из запоя краснодар
narkolog-krasnodar003.ru
вывод из запоя круглосуточно
экстренный вывод из запоя
narkolog-krasnodar003.ru
экстренный вывод из запоя
Переезд в столицу — это необычно непростое событие, особенно когда речь идет о доступе к интернету и телевидению. При смене места жительства важно учесть выбор провайдера, так как услуги интернета могут различаться в зависимости от местоположения. В Екатеринбурге доступен разнообразие интернет-провайдеров, предлагающих различные тарифы на интернет. Оптоволоконное соединение обеспечивает высокую скорость и стабильность соединения, что особенно актуально для работы из дома; Беспроводной интернет также может быть полезным выбором, но его скорость чаще всего ниже. телевидение и интернет Екатеринбург При перемещении стоит сравнить провайдеров по параметрам, таким как качество интернета, стоимость подключения и наличие акций и скидок. Не забудьте изучить отзывы о провайдерах — они помогут вам избежать проблем. Установка интернета и кабельного телевидения обычно осуществляется быстро, но лучше заранее поинтересоваться сроками подключения и необходимых документах. Важно выбрать надежного провайдера, чтобы наслаждаться качественными услугами интернета и телевидения в Екатеринбурге.
https://vc.ru/niksolovov/1555291-besplatnaya-nakrutka-laikov-vkontakte-25-servisov-i-metodov-v-2025-godu
be many ways set out,ラブドール オナニーand expressed.
вывод из запоя
narkolog-krasnodar004.ru
экстренный вывод из запоя
At last I got the better of him.フィギュア 無 修正He left off clankingit.
Adventure Island Rohini is a popular amusement park in New Delhi, offering exciting rides, water attractions, and entertainment for all ages: family activities at Adventure Island
вывод из запоя круглосуточно
narkolog-krasnodar004.ru
вывод из запоя цена
В столице России представлено множество интернет-провайдеров, которые предоставляют услуги для корпоративного сегмента. Выбор провайдера — ключевой момент для гарантии надежного соединения и качественного интернет-сервиса. Надежные провайдеры предлагают различные тарифы на интернет, которые учитывают потребности компаний.Скорость интернета — важный фактор, который напрямую влияет на продуктивность работы. Многие интернет-провайдеры предлагают корпоративный интернет с высокоскоростными тарифами, что идеально подходит для крупных коллективов. Услуги для бизнеса также могут включать интернет-решения, обеспечивающие безопасность и надежность при подключении к сети. провайдеры интернета в Екатеринбурге При выборе провайдера стоит обратить внимание на репутацию провайдера связи. Это поможет найти надежного партнера для вашего бизнеса в Екатеринбурге в Екатеринбурге.
Копался по теме пневматики и охоты, нашёл неплохой форум с обсуждениями и советами. Вдруг кому будет полезно: https://guns.allzip.org/topic/56/218719.html
вывод из запоя круглосуточно краснодар
narkolog-krasnodar005.ru
лечение запоя краснодар
лечение запоя краснодар
narkolog-krasnodar005.ru
вывод из запоя круглосуточно
Как выбрать интернет для дома в Екатеринбурге: важные аспекты При поиске интернета для квартиры важно обратить внимание на несколько факторов. Первым делом стоит обратить внимание на интернет-провайдеров, предоставляющих услуги связи в Екатеринбурге. Сравнение тарифов на интернет поможет найти оптимальный вариант. Скорость интернета — ключевой фактор. Для комфортного использования безлимитного интернета нужна высокая скорость, особенно если в доме несколько пользователей. Интернет по оптоволокну гарантирует быструю и надежную связь. Обязательно ознакомьтесь с отзывами о провайдерах. Это даст представление о качестве связи и стабильности интернета. Также стоит изучить дополнительные предложения, например, установку Wi-Fi роутеров. domashij-internet-ekaterinburg006.ru Выбор провайдера не должен быть спонтанным. Внимательно рассмотрите все детали, чтобы сделать правильный выбор для вашего интернета дома.
Наркологическая помощь доступна в любое время на сайте narkolog-tula001.ru. Терапия наркомании требует квалифицированного подхода‚ и наша команда готова предоставить консультацию нарколога в любое время. Мы поддерживаем зависимым‚ предоставляя анонимное лечение и реабилитационный центр для восстановления после зависимости. Наша detox программа включает психотерапевтическую помощь и медицинскую помощь при алкоголизме. Мы также обеспечиваем профилактику рецидивов через индивидуальную терапию и кризисную интервенцию. Не ждите‚ обратитесь за помощью уже сегодня!
Помощь наркологов в Туле доступна для всех, кто встретился с проблемами зависимости; Анонимная помощь — это ключевой момент, дающий возможность пациентам обращаться без страха осуждения. Наркологическая клиника предоставляет лечение зависимости через персонализированные программы реабилитации. Первичная консультация у нарколога — первый шаг к исцелениюгде можно узнать детали о detox-программах и психологической поддержке. Реабилитация включает семейную терапию, что способствует успешному лечению и профилактике рецидива. Свяжитесь на narkolog-tula001.ru для получения анонимного лечения и услуг.
какие провайдеры по адресу
domashij-internet-kazan004.ru
провайдеры интернета по адресу
Клиники Тулы предлагают разнообразные пакеты услуг, включая инъекции для снятия запойного состояния, которые могут включать витамины и препараты для снятия симптомов. Сравнение клиник позволяет выбрать наиболее подходящий вариант с учетом ценовой политики и уровня сервиса. Большинство учреждений предоставляет круглосуточную помощь в большинстве учреждений.При выборе клиники стоит учитывать отзывы пациентов и опыт врачей. Консультации нарколога помогут составить эффективный план терапии алкоголизма. Конфиденциальное лечение также является значимым фактором, так как некоторые пациенты хотят сохранить анонимность.После завершения запойного состояния требует успешной комплексной терапии, включая реабилитацию алкоголиков и дальнейшее наблюдение за состоянием пациента. Таким образом, услуги нарколога, такие как вывод из запоя и капельницы от запоя, играют важную роль в процессе восстановления. вывод из запоя круглосуточно тула
Прокапаться от алкоголя на дому — значимый этап для преодоления алкогольной зависимости. Лечение алкоголизма начинается с детоксикации , которая может быть проведена в домашних условиях . Основные подходы включают использование медикаментов и поддержку специалистов, которые помогут безопасно прекратить употребление . narkolog-tula002.ru Рекомендации для поддержания трезвости и стратегии преодоления зависимости, такие как самопомощь при алкоголизме , играют ключевую роль в процессе восстановления. Безопасное прекращение употребления алкоголя — это шаг к новой, трезвой жизни.
интернет по адресу дома
domashij-internet-kazan005.ru
интернет по адресу казань
Выездной нарколог – это прекрасная возможность для тех, кто сталкивается с алкогольной зависимостью или наркоманией. Терапия зависимостей включает в себя очистку организма и реабилитацию зависимых. Нарколог на дому предоставляет анонимное лечение, что особенно важно для пациентов, стыдящихся обращаться в клинику. Методы кодирования – проверенный способ, который можно провести на дому. Помощь на дому включает в себя психологическую поддержку и медицинскую помощь. Консультации специалиста помогут понять, как преодолеть зависимости. Реабилитационные программы и семейная терапия играют ключевую роль в процессе лечения. На сайте narkolog-tula003.ru вы найдете подробности о доступных услугах.
Детоксикация от алкоголя – это ключевой этап в борьбе с алкоголизмом‚ но вокруг нее существует множество мифов. Первый миф: вывод из запоя цена высока. На самом деле стоимость лечения алкоголизма варьируются‚ и доступные программы detox предлагают разные варианты. Второй миф: симптомы запойного состояния неопасны. Запой может привести к алкогольным отравлениям и серьезным последствиям. вывод из запоя цена Лечение запойного состояния включает в себя детоксикацию организма и психотерапевтическую помощь. Реабилитация после алкоголя важна для восстановления и социальной адаптации. Осознание заблуждений о процессе детоксикации позволяет избежать ошибок на пути к выздоровлению.
провайдеры интернета по адресу
domashij-internet-kazan006.ru
провайдеры интернета по адресу казань
Наркологическая помощь в Туле 24/7 – это существенная часть процесса выздоровления от зависимости. В клиниках наркологии, таких как narkolog-tula004.ru, предоставляется анонимное лечение и консультация нарколога. Профессиональная команда врачей предлагает программу по очищению организма, чтобы помочь пациентам освободиться от физической зависимости. Лечение наркозависимости в стационаре включает психотерапию, а также помощь для близких. Организация медицинской помощи в Туле направлена на профилактику наркотиков и быструю реакцию в кризисных ситуациях. Услуги нарколога доступны круглосуточно, что позволяет быстро реагировать на запросы и гарантировать пациентам требуемую поддержку.
Капельница от запоя – это проверенный способ терапии алкоголизма‚ который реализует нарколог с выездом на дом. Этапы подготовки к процедуре включает несколько этапов. Первым делом‚ важно проанализировать симптомы запоя: головные боли‚ повышенная тревожность‚ обильное потоотделение. Затем пациент должен подготовить комфортное место для процедуры‚ где будет возможен доступ к венам. Услуги на дому даёт возможность устранить стресс‚ который возникает при визите в клинику. Специалист проведет очищение организма‚ вводя лечебные растворы‚ которые нормализуют состояние организма и повышают общее самочувствие. Эффективность капельницы заключается в оперативном удалении токсинов и облегчении состояния. Помимо этого‚ уколы от запоя могут дополнительно помочь в стабилизации состояния. После процедуры начинается программа реабилитации‚ направленная на избежание повторных случаев. врач нарколог на дом
проверить провайдера по адресу
domashij-internet-krasnoyarsk004.ru
интернет по адресу дома
Наркология – это важная область медицины‚ ориентированная на лечение зависимостями. Если вы или ваши близкие переживаете проблемы зависимости от наркотиков‚ важно знать о возможностях анонимного лечения. Специализированные клиники, такие как narkolog-tula004.ru‚ предоставляют поддержку нарколога и всестороннюю поддержку для зависимых. Поддерживающие сообщества и программы восстановления оказывают помощь людям на этапе к выздоровлению. Психологическая помощь при зависимости занимает ключевую роль в восстановлении наркозависимых. Также существенна профилактика наркомании и экстренная поддержка. Не бойтесь обращаться за помощью — вы можете вернуться к нормальной жизни!
Как провести ремонт и улучшить свое жилье самостоятельно Когда дом нуждается в ремонте, помощь специалистов может оказаться очень кстати; На сайте narkolog-tula006.ru вы найдете множество домашних мастеров, готовых помочь с устранением неисправностей. Это может быть как мелкий ремонт, так и более серьезные сантехнические работы или электромонтажные услуги. Для самостоятельного ремонта существуют несколько ключевых рекомендаций. Первый шаг — это планирование: определите, какие именно работы нужно выполнить, и составьте детальную смету. Также не забывайте о безопасности при выполнении электромонтажных работ. Для декорирования вашего жилья обратитесь к домашним умельцам, которые предоставляют услуги по благоустройству. Эти специалисты смогут сделать ваш дом более уютным и привлекательным. Не забывайте, что качественный ремонт, это залог вашего комфорта и уюта!
провайдеры интернета по адресу красноярск
domashij-internet-krasnoyarsk005.ru
провайдер по адресу красноярск
Капельницы для лечения запоя в Туле: быстрая помощь Алкоголизм — серьезная проблема‚ требующая внимания и профессиональной помощи. В Туле наблюдается рост спроса на услуги нарколога на выезд. Специалисты-наркологи на дом в Туле предоставляют экстренные услуги‚ включая детоксикацию и помощь при запое.Капельницы являются одним из наиболее действенных способов борьбы с запоем. Данный метод снабжает организм важными веществами‚ что способствует быстрому очищению. Специализированная помощь нарколога включает в себя терапевтические процедуры‚ которые помогают справиться с физической зависимостью от спиртного. нарколог на дом тула Главное‚ не откладывать вызов нарколога на дом. Чем быстрее начнется лечение алкогольной зависимости‚ тем выше шансы на успешное восстановление. Нарколог на дом предоставляет возможность получить своевременную помощь без поездки в медицинское учреждение. Мы поможем вам справиться с зависимостью от алкоголя.
Капельница для лечения алкоголизма – это действующий способ‚ который оказать помощь в реабилитации после алкогольной зависимости в домашних условиях. Вызвав к наркологу‚ который приедет к вам‚ вы сможете получить квалифицированную помощь и необходимые медикаменты для облегчения симптомов похмелья. Признаки запойного состояния могут включать головной боли‚ недомогания и общего недомогания; вызвать нарколога на дом тула Этап очистки организма начинается с введения капельницы‚ что обеспечивает поступление жидкости и витаминов‚ что помогает снять симптомы абстиненции. Услуги нарколога в Туле включают персонализированный подход к пациенту‚ что важно для успешного лечения алкоголизма в домашних условиях. Поддержка близких при алкоголизме является важной составляющей в процессе восстановления здоровья после алкоголя. Домашняя реабилитация осуществляется с помощью препаратов и капельниц‚ что позволяет предотвратить новые запои и облегчить процесс восстановления. При этом профилактика запоев является ключевым моментом в борьбе с зависимостью.
הגיל כבר? טרנסג ‘ נדרים, איך אתה משדל בעלים למציצות? לנה וובה היו זוג נשוי כמעט מושלם שלנו, ” אני כאן, זה בסדר.” למה שלא נרקוד? – מציעה קטיה וקולה נשמע קל, אך עם צרידות קלה, The best escort girls show sexuality
провайдеры интернета по адресу красноярск
domashij-internet-krasnoyarsk006.ru
интернет по адресу красноярск
Наркологическая служба в Туле – это неотъемлемая часть борьбы с алкоголизмом и наркотической зависимостью. На сайте narkolog-tula006.ru можно получить доступных услугах, таких как вызов нарколога на дом при зависимости от алкоголя и различных видах наркозависимости. Наркологическая помощь включает консультации специалистов, стационарное лечение и программы реабилитации.Медицинская помощь направлена на восстановление психического здоровья и терапию зависимости. Не упустите шанс на выздоровление, свяжитесь с нами сегодня!
пансионат инсульт реабилитация
pansionat-msk001.ru
пансионат для лежачих пожилых
узнать интернет по адресу
domashij-internet-krasnodar004.ru
какие провайдеры по адресу
אירינה במגבת, על פי הטקס, שטפתי את פני במים מהאגן, ואפילו שתיתי ממנו. לשטוף את הרגליים מרשים, פחדה להתגלגל מהמגלשה הגבוהה. טיכון, שישב לצדה, תפס אותה בחזה הזה. למה היא הלכה למטה this article
кашпо для цветов напольное вазон [url=www.kashpo-napolnoe-spb.ru]www.kashpo-napolnoe-spb.ru[/url] .
пансионат для лежачих пожилых
pansionat-msk002.ru
пансионаты для инвалидов в москве
Обращение за помощью нарколога в Туле – ключевой шаг для тех‚ кто с трудностями зависимости. На сайте narkolog-tula007.ru вы имеете возможность получить квалифицированной помощью. Наркологическая помощь включает определение зависимости и конфиденциальное лечение. Если у вас возникли алкогольная или наркотическая зависимость‚ срочный вызов врача поможет избежать последствий. Центры реабилитации предлагают программы восстановления и поддержку семьи‚ что является важным для успешного лечения. Консультация нарколога – это первый этап на пути к исцелению. Не откладывайте‚ обратитесь за медицинской помощью уже сегодня!
провайдеры интернета в краснодаре по адресу проверить
domashij-internet-krasnodar005.ru
узнать интернет по адресу
пансионат для людей с деменцией в москве
pansionat-msk003.ru
пансионат инсульт реабилитация
какие провайдеры по адресу
[url=https://domashij-internet-krasnodar006.ru]domashij-internet-krasnodar006.ru[/url]
интернет провайдеры по адресу
пансионат для престарелых людей
pansionat-msk001.ru
пансионат для пожилых с деменцией
пансионат для лежачих больных
pansionat-tula001.ru
пансионат для пожилых
В столице России множество интернет-провайдеров, которые предлагают самые разные тарифы на интернет. Выбирая провайдера важно учитывать доступность сети и скорость интернета, чтобы обеспечить качественный интернет для дома или бизнеса. Сравнение провайдеров, можно выявить наилучшие предложения. К примеру, domashij-internet-msk004.ru предлагает детальные отзывы о провайдерах и их рейтинги. Это поможет вам сделать осознанный выбор. Не забудьте также обратить внимание на услуги связи, включая интернет-подключение и Wi-Fi для жилища. Стабильное соединение и доступ в интернет – важнейшие аспекты для комфортного использования. Не забывайте проверять актуальные тарифы на интернет и условия подключения.
пансионат инсульт реабилитация
pansionat-msk002.ru
пансионат для престарелых людей
пансионат для лежачих пожилых
pansionat-tula002.ru
пансионат с деменцией для пожилых в туле
Определение интернет-провайдера в Москве для игр — задача , которая не из простых. Множество игроков хотят к высокоскоростному интернету с низкой задержкой и надежным подключением. Операторы интернета по адресу в Москве имеют различные тарифы на интернет, включая оптоволоконный интернет , который является отличным вариантом для любителей игр. Анализ провайдеров поможет вам выбрать наиболее подходящий вариант. Обратите внимание отзывы о провайдерах, чтобы отобрать достойного оператора связи. Также стоит рассмотреть возможности использования VPN для игр, что может повысить качество соединения. Для игроков онлайн важно, чтобы интернет был стабильным и скоростным. Исследуйте предложения операторов, чтобы найти идеальный интернет в Москве для ваших потребностей.
частный пансионат для пожилых
pansionat-msk003.ru
частный дом престарелых
пансионат для людей с деменцией в туле
pansionat-tula003.ru
пансионат для пожилых
декоративный горшок напольный для цветов [url=http://kashpo-napolnoe-msk.ru/]http://kashpo-napolnoe-msk.ru/[/url] .
вывод из запоя челябинск
[url=https://vivod-iz-zapoya-chelyabinsk001.ru]https://vivod-iz-zapoya-chelyabinsk001.ru[/url]
вывод из запоя круглосуточно
пансионат инсульт реабилитация
pansionat-tula001.ru
пансионат для престарелых людей
провайдеры интернета нижний новгород
domashij-internet-nizhnij-novgorod004.ru
домашний интернет в нижнем новгороде
вывод из запоя круглосуточно
vivod-iz-zapoya-chelyabinsk002.ru
вывод из запоя
You deserve it all.I should not besorry to see you disgraced,lovedoll
пансионат для реабилитации после инсульта
pansionat-tula002.ru
пансионат для лежачих тула
провайдеры в нижнем новгороде по адресу проверить
domashij-internet-nizhnij-novgorod005.ru
провайдеры по адресу дома
экстренный вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk003.ru
экстренный вывод из запоя челябинск
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Ознакомиться с деталями – https://vyvod-iz-zapoya-1.ru/
Neil Island is a small, peaceful island in the Andaman and Nicobar Islands, India. It’s known for its beautiful beaches, clear blue water, and relaxed atmosphere: how to reach Neil Island
частные пансионаты для пожилых в туле
pansionat-tula003.ru
пансионат инсульт реабилитация
подключить интернет по адресу
domashij-internet-nizhnij-novgorod006.ru
провайдер по адресу нижний новгород
вывод из запоя череповец
vivod-iz-zapoya-cherepovec004.ru
вывод из запоя цена
лечение запоя челябинск
[url=https://vivod-iz-zapoya-chelyabinsk001.ru]https://vivod-iz-zapoya-chelyabinsk001.ru[/url]
экстренный вывод из запоя
При подборе интернета для большой семьи в новосибирске важно учитывать несколько аспектов. Во-первых‚ интернет-скорость должна быть высокой‚ чтобы все члены семьи могли в одно и то же время использовать интернет. Рекомендуется изучить семейные тарифы от интернет-провайдеров‚ которые предлагают неограниченный доступ к интернету и стабильное соединение. domashij-internet-novosibirsk004.ru Анализ провайдеров поможет выбрать лучший вариант‚ основываясь на отзывах пользователей. Домашние роутеры также играют важную роль‚ так как Wi-Fi для большой семьи должен охватывать все уголки квартиры. Не забывайте про IPTV для семьи‚ который может стать отличным источником развлечений. Выбирая тариф обращайте внимание на скидки для семей и акции. Подключение интернета должно быть быстрым и удобным‚ чтобы не терять время в ожидании. Сотовый интернет также может оказаться полезным в поездках. Услуги связи в новосибирске предлагают множество вариантов‚ так что принимайте обоснованные решения!
вывод из запоя череповец
vivod-iz-zapoya-cherepovec005.ru
вывод из запоя череповец
вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk002.ru
экстренный вывод из запоя
Установка фиксированного интернет-соединения в столице стало актуальной проблемой для многих жителей . Высокоскоростной интернет в новосибирске предлагает скорость , которая способна удовлетворить даже самых требовательных пользователей . Провайдеры новосибирска предлагают различные тарифы на доступ в сеть, включая в себя выгодные предложения с гигабитными скоростями. Гигабитный интернет в новосибирске При выборе провайдера необходимо обращать внимание на отзывы о провайдерах , так как надежность соединения и качество обслуживания – ключевые факторы . Многие компании предоставляют услуги подключения интернета по технологии FTTH, что обеспечивает высокую скорость и надежность . Анализ предложений провайдеров поможет выбрать наилучший вариант для вашего дома . Обратите внимание на наличие Wi-Fi роутеров в комплекте , а также на качество клиентской поддержки. Подбирайте оптимальный интернет для вашего дома и получайте удовольствие от стабильного соединения!
вывод из запоя череповец
vivod-iz-zapoya-cherepovec006.ru
вывод из запоя круглосуточно череповец
купить напольное кашпо недорого высокие недорого [url=https://kashpo-napolnoe-rnd.ru]купить напольное кашпо недорого высокие недорого[/url] .
the oak is right,a thousand times right,ラブドール 中出し
Мобильный интернет в новосибирске: обзор операторов В столице России мобильный интернет стал неотъемлемой частью жизни. Основные операторы связи предлагают широкие тарифы на мобильный интернет, включая пакетные предложения и ограниченные опции. Рассмотрим главные факторы выбора провайдера. Скорость интернета – важный фактор. В новосибирске доступны технологии четвертого поколения и 5G, которые обеспечивают высокую скорость соединения. Операторы связи, такие как Мобилочка, Билайн, Мегафон и Теле 2, активно развивают зоны покрытия, предлагая своим клиентам стабильное качество связи. При выборе интернет-провайдеров в новосибирске по адресу необходимо обратить внимание на отзывы о провайдерах. Пользователи обращают внимание на различия в качестве связи и скорости интернета, что влияет на их выбор. интернет провайдеры в новосибирске по адресу Обзор тарифов на мобильный интернет помогает найти лучшие предложения. Многие операторы предлагают специальные предложения, которые могут включать дополнительные мобильные пакеты данных или привлекательные тарифы для новых пользователей.
экстренный вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk003.ru
вывод из запоя цена
лечение запоя
vivod-iz-zapoya-irkutsk001.ru
вывод из запоя цена
https://ernestz862lpr4.wikiparticularization.com/user
домашний интернет подключить омск
domashij-internet-omsk004.ru
подключить интернет омск
вывод из запоя череповец
vivod-iz-zapoya-cherepovec004.ru
экстренный вывод из запоя
цветочные горшки большие напольные пластиковые [url=kashpo-napolnoe-rnd.ru]цветочные горшки большие напольные пластиковые[/url] .
Студия дизайна Интерьеров в СПБ. Лучшие условия для заказа и реализации дизайн-проектов под ключ https://cr-design.ru/
вывод из запоя цена
vivod-iz-zapoya-irkutsk003.ru
лечение запоя
подключить интернет омск
domashij-internet-omsk005.ru
провайдеры интернета омск
вывод из запоя цена
vivod-iz-zapoya-cherepovec005.ru
вывод из запоя круглосуточно череповец
лечение запоя
vivod-iz-zapoya-kaluga004.ru
лечение запоя
подключить интернет в квартиру омск
domashij-internet-omsk006.ru
домашний интернет тарифы
лечение запоя
vivod-iz-zapoya-cherepovec006.ru
вывод из запоя цена
вывод из запоя круглосуточно
vivod-iz-zapoya-kaluga005.ru
экстренный вывод из запоя калуга
тарифы интернет и телевидение пермь
domashij-internet-perm004.ru
лучший интернет провайдер пермь
экстренный вывод из запоя иркутск
vivod-iz-zapoya-irkutsk001.ru
вывод из запоя цена
вывод из запоя цена
vivod-iz-zapoya-kaluga006.ru
лечение запоя калуга
тарифы интернет и телевидение пермь
domashij-internet-perm005.ru
подключить интернет в квартиру пермь
лечение запоя
vivod-iz-zapoya-krasnodar001.ru
экстренный вывод из запоя краснодар
экстренный вывод из запоя
vivod-iz-zapoya-irkutsk002.ru
вывод из запоя
интернет тарифы пермь
domashij-internet-perm006.ru
домашний интернет тарифы пермь
вывод из запоя круглосуточно краснодар
vivod-iz-zapoya-krasnodar002.ru
вывод из запоя круглосуточно краснодар
лечение запоя
vivod-iz-zapoya-irkutsk003.ru
вывод из запоя
интернет домашний ростов
domashij-internet-rostov004.ru
дешевый интернет ростов
вывод из запоя круглосуточно
vivod-iz-zapoya-krasnodar003.ru
лечение запоя
лечение запоя калуга
vivod-iz-zapoya-kaluga004.ru
вывод из запоя круглосуточно
подключить интернет
domashij-internet-rostov005.ru
подключение интернета ростов
Наш агрегатор – beautyplaces.pro собирает лучшие салоны красоты, СПА, центры ухода за телом и студии в одном месте. Тут легко найти подходящие услуги – от стрижки и маникюра до косметологии и массажа – с удобным поиском, подробными отзывами и актуальными акциями. Забронируйте визит за пару кликов https://beautyplaces.pro/
экстренный вывод из запоя
vivod-iz-zapoya-krasnodar004.ru
вывод из запоя цена
напольные высокие горшки для цветов цены [url=http://kashpo-napolnoe-rnd.ru]http://kashpo-napolnoe-rnd.ru[/url] .
вывод из запоя круглосуточно калуга
vivod-iz-zapoya-kaluga005.ru
вывод из запоя
провайдеры интернета ростов
domashij-internet-rostov006.ru
домашний интернет в ростове
экстренный вывод из запоя
vivod-iz-zapoya-krasnodar005.ru
экстренный вывод из запоя краснодар
вывод из запоя круглосуточно калуга
vivod-iz-zapoya-kaluga006.ru
вывод из запоя круглосуточно
провайдеры по адресу дома
domashij-internet-samara004.ru
какие провайдеры интернета есть по адресу самара
Наркология в Красноярске предлагает разнообразные услуги для людей‚ страдающих от различных зависимостей. Важно понимать‚ что преодоление зависимости — это сложный процесс. Первый этап — это встреча с наркологом‚ который выяснит степень зависимости и подберет наиболее подходящее лечение. В Красноярске функционируют кризисные центры‚ где можно получить конфиденциальную помощь специалистов. Психотерапевтические методы помогают в восстановлении. Семейная терапия способствует улучшению отношений и поддерживает пациента. Реабилитация наркоманов включает программы лечения алкоголизма и помощь с наркотиками. Важно знать о профилактических мерах и следовать рекомендациям специалистов. Восстановление после зависимости — это длительный процесс‚ требующий терпения и поддержки. Свяжитесь с клиникой зависимостей на vivod-iz-zapoya-krasnoyarsk001.ru для профессиональной помощи.
Предлагаем вашему вниманию интересную справочную статью, в которой собраны ключевые моменты и нюансы по актуальным вопросам. Эта информация будет полезна как для профессионалов, так и для тех, кто только начинает изучать тему. Узнайте ответы на важные вопросы и расширьте свои знания!
Углубиться в тему – https://www.hotel-sugano.com/bbs/sugano.cgi/sosh13.pascal.ru/forum/datasphere.ru/club/user/12/blog/2477/www.tovery.net/sinopipefittings.com/e_Feedback/sinopipefittings.com/e_Feedback/www.hip-hop.ru/forum/id298234-worksale
В обзорной статье вы найдете собрание важных фактов и аналитики по самым разнообразным темам. Мы рассматриваем как современные исследования, так и исторические контексты, чтобы вы могли получить полное представление о предмете. Погрузитесь в мир знаний и сделайте шаг к пониманию!
Изучить вопрос глубже – https://majesticvillas.gr/porto-katsiki-beach-in-lefkada
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Ознакомиться с деталями – https://latinloyalty.com/hello-world
В этой статье-обзоре мы соберем актуальную информацию и интересные факты, которые освещают важные темы. Читатели смогут ознакомиться с различными мнениями и подходами, что позволит им расширить кругозор и глубже понять обсуждаемые вопросы.
Изучить вопрос глубже – https://fisioterapia-alcala126.com/20-anos-centro-fisioterapia-alcala
В этой статье собраны факты, которые освещают целый ряд важных вопросов. Мы стремимся предложить читателям четкую, достоверную информацию, которая поможет сформировать собственное мнение и лучше понять сложные аспекты рассматриваемой темы.
Ознакомиться с деталями – https://vistoweekly.com/mastering-rubranking-for-seo-success-in-digital-marketing
Профессиональная наркологическая клиника. Лечение зависимостей, капельницы, вывод из запоя, реабилитация. Анонимно, круглосуточно, с поддержкой врачей и психологов.
В этой публикации мы предлагаем подробные объяснения по актуальным вопросам, чтобы помочь читателям глубже понять их. Четкость и структурированность материала сделают его удобным для усвоения и применения в повседневной жизни.
Углубиться в тему – https://seikou-church.net/2024/06/02/%E7%A4%BC%E6%8B%9D%E3%81%AE%E9%96%8B%E5%A7%8B%E6%99%82%E9%96%93%E3%81%8C%E5%A4%89%E3%82%8F%E3%82%8A%E3%81%BE%E3%81%99
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Подробнее можно узнать тут – https://gioiosabergamo.it/home-default/play
какие провайдеры на адресе в самаре
domashij-internet-samara005.ru
интернет провайдеры самара по адресу
вывод из запоя краснодар
vivod-iz-zapoya-krasnodar001.ru
лечение запоя краснодар
Платная наркологическая помощь в Красноярске набирает популярность. Наркологические клиники, такие как наркологическая клиника Красноярск предлагают широкий спектр услуг: от детоксикации организма до реабилитации наркозависимых. Психотерапия и консультирование по зависимостям помогают пациентам понять психологию зависимости и находить пути к выздоровлению. Алкогольные реабилитационные центры предлагают конфиденциальное лечение и персонализированный подход к каждому клиенту. Квалифицированные специалисты в области наркологии, реабилитационные программы и медицинское сопровождение при лечении зависимостей играют ключевую роль в успешной реабилитации. Социальная адаптация после лечения имеет большое значение для снижения риска рецидивов. Дополнительные сведения доступны на сайте vivod-iz-zapoya-krasnoyarsk002.ru.
проверить провайдеров по адресу самара
domashij-internet-samara006.ru
интернет провайдеры по адресу
Наркологическая помощь становится актуальной в преодолении зависимостей. На сайте vivod-iz-zapoya-krasnoyarsk003.ru можно найти информация о программах реабилитации, включая индивидуальные подходы. Квалифицированные специалисты поддерживают в выявлении проблем с зависимостями и рекомендуют медицинскую помощь при алкоголизме и наркомании. Первичная консультация — это первый шаг к избавлению от зависимости после зависимости. Важны подходы к предотвращению рецидивов и семейная терапия для поддержки в процессе реабилитации. Забота со стороны семьи и врачей помогает преодолеть трудности на пути к здоровой жизни.
лечение запоя
vivod-iz-zapoya-krasnodar002.ru
вывод из запоя круглосуточно краснодар
подключение интернета по адресу
domashij-internet-spb004.ru
провайдеры интернета в санкт-петербурге
вывод из запоя круглосуточно минск
vivod-iz-zapoya-minsk001.ru
вывод из запоя минск
лечение запоя
vivod-iz-zapoya-krasnodar003.ru
экстренный вывод из запоя краснодар
какие провайдеры интернета есть по адресу санкт-петербург
domashij-internet-spb005.ru
проверить провайдера по адресу
вывод из запоя круглосуточно минск
vivod-iz-zapoya-minsk002.ru
лечение запоя
вывод из запоя цена
vivod-iz-zapoya-krasnodar004.ru
лечение запоя
недорогой интернет санкт-петербург
domashij-internet-spb006.ru
какие провайдеры на адресе в санкт-петербурге
лечение запоя минск
vivod-iz-zapoya-minsk003.ru
вывод из запоя
В этой статье собраны факты, которые освещают целый ряд важных вопросов. Мы стремимся предложить читателям четкую, достоверную информацию, которая поможет сформировать собственное мнение и лучше понять сложные аспекты рассматриваемой темы.
Не пропусти важное – https://www.slovcar.sk/2022/11/13/stories-about-digital-marketing-2
Этот текст сочетает в себе элементы познавательного рассказа и аналитической подачи информации. Читатель получает доступ к уникальным данным, которые соединяют прошлое с настоящим и открывают двери в будущее.
Все материалы собраны здесь – https://savaherbals.in/liver-detox
В этой статье вы найдете познавательную и занимательную информацию, которая поможет вам лучше понять мир вокруг. Мы собрали интересные данные, которые вдохновляют на размышления и побуждают к действиям. Открывайте новую информацию и получайте удовольствие от чтения!
Обратиться к источнику – https://steigensynergy.com/steigen-synergy-it-is-now-an-sap-partner
В этой статье представлен занимательный и актуальный контент, который заставит вас задуматься. Мы обсуждаем насущные вопросы и проблемы, а также освещаем истории, которые вдохновляют на действия и изменения. Узнайте, что стоит за событиями нашего времени!
Более подробно об этом – https://babi-beauty.fr/signature-styles-the-best-haircuts-at-our-barber-shop
Эта статья предлагает живое освещение актуальной темы с множеством интересных фактов. Мы рассмотрим ключевые моменты, которые делают данную тему важной и актуальной. Подготовьтесь к насыщенному путешествию по неизвестным аспектам и узнайте больше о значимых событиях.
Заходи — там интересно – https://cheerleader-verein-dresden.de/portfolio/oxygen-club-national-meets-in-2000s
В этой публикации мы предлагаем подробные объяснения по актуальным вопросам, чтобы помочь читателям глубже понять их. Четкость и структурированность материала сделают его удобным для усвоения и применения в повседневной жизни.
Узнать напрямую – https://sepidsanat.com/%D9%86%D8%B5%D8%A8-%D8%B3%DB%8C%D9%86%DB%8C-%D9%87%D8%A7%DB%8C-%DA%A9%D8%A7%D8%A8%D9%84
лечение запоя краснодар
vivod-iz-zapoya-krasnodar005.ru
экстренный вывод из запоя краснодар
В этом информативном тексте представлены захватывающие события и факты, которые заставят вас задуматься. Мы обращаем внимание на важные моменты, которые часто остаются незамеченными, и предлагаем новые перспективы на привычные вещи. Подготовьтесь к тому, чтобы быть поглощенным увлекательными рассказами!
Следуйте по ссылке – https://f5fashion.vn/top-voi-hon-67-ve-xe-lexus-lx570-hay-nhat
Эта статья предлагает живое освещение актуальной темы с множеством интересных фактов. Мы рассмотрим ключевые моменты, которые делают данную тему важной и актуальной. Подготовьтесь к насыщенному путешествию по неизвестным аспектам и узнайте больше о значимых событиях.
Более того — здесь – http://www.all-hit.ru
экстренный вывод из запоя
vivod-iz-zapoya-omsk001.ru
вывод из запоя круглосуточно
В этой статье собраны факты, которые освещают целый ряд важных вопросов. Мы стремимся предложить читателям четкую, достоверную информацию, которая поможет сформировать собственное мнение и лучше понять сложные аспекты рассматриваемой темы.
Узнать напрямую – https://almaxindustry.com/komatsu-pump-list
интернет по адресу дома
domashij-internet-ufa004.ru
интернет провайдеры в уфе по адресу дома
Специалист по наркологии — это медицинский работник, который предоставляет помощь людям, испытывающим проблемы от алкоголизма и наркомании. Процесс лечения включает в себя детоксикацию, медикаменты и психотерапию. Важно обратиться за консультацией нарколога для определения персонализированного подхода реабилитации. Семейная поддержка играет важную роль в процессе выздоровления, а группы взаимопомощи помогают интегрироваться в социальной среде. Профилактика зависимостей также имеют значение, чтобы снизить риск рецидивов. Обращение к профессионалам на vivod-iz-zapoya-krasnoyarsk001.ru гарантирует качественную медицинскую помощь и содействие на всех этапах лечения.
экстренный вывод из запоя омск
vivod-iz-zapoya-omsk002.ru
лечение запоя омск
интернет провайдеры в уфе по адресу дома
domashij-internet-ufa005.ru
интернет по адресу дома
Выездная наркологическая помощь – это неотъемлемая часть лечения зависимостей‚ который предоставляет экстренную помощь при алкоголизме и зависимости от наркотиков. Служба наркологической помощи на выезд предоставляет профессиональную помощь зависимым‚ включая детоксикацию и кризисную интервенцию. На сайте vivod-iz-zapoya-krasnoyarsk002.ru можно получить консультации по наркологии‚ ознакомиться с методами лечения наркомании и реабилитации на дому. Конфиденциальное лечение зависимых позволяет сохранить конфиденциальность. Важно также помнить о поддержке близких‚ что способствует в процессе восстановления. Программа восстановления после зависимости включает профилактику зависимостей и психотерапию‚ что способствует успешному возвращению к нормальной жизни.
лечение запоя
vivod-iz-zapoya-omsk003.ru
лечение запоя омск
провайдеры по адресу
domashij-internet-ufa006.ru
провайдеры интернета по адресу уфа
Капельница от запоя – это один из наиболее эффективных методов лечения алкогольной зависимости‚ который обеспечивает возможность комфортного и конфиденциального лечения. Нарколог на дом анонимно может быстро обеспечить необходимую медицинскую помощь при запое‚ используя метод капельницы для очищения организма. Преимущества капельницы заключаются в том‚ что она способствует быстрому снятию симптомов запоя‚ восстанавливает баланс жидкости и электролитов и способствует улучшению общего состояния пациента. Это особенно важно в случае тяжелых стадий алкоголизма‚ когда требуется срочное вмешательство.Существуют различные методы лечения алкоголизма‚ но капельница выделяется своей эффективностью и скоростью. В сравнении с таблетками и инъекциями‚ капельница гарантирует непрерывное введение медикаментов в организм‚ что способствует более быстрому восстановлению.Поддержка семьи и психотерапия при алкоголизме также играют важную роль в процессе реабилитации. По завершении этапа детоксикации важно продолжать лечение и заниматься профилактикой рецидивов‚ что возможно только при комплексном подходе. Таким образом‚ капельница при запое — это ключевой элемент в борьбе с алкоголизмом‚ предоставляя пациентам эффективное и конфиденциальное лечение с быстрым восстановлением.
вывод из запоя цена
vivod-iz-zapoya-orenburg001.ru
лечение запоя
подключить интернет в волгограде в квартире
domashij-internet-volgograd004.ru
домашний интернет тарифы омск
лечение запоя
vivod-iz-zapoya-minsk001.ru
экстренный вывод из запоя минск
вывод из запоя
vivod-iz-zapoya-orenburg002.ru
экстренный вывод из запоя
домашний интернет тарифы
domashij-internet-volgograd005.ru
интернет провайдеры омск
”You could see the superstitious crowd shrink and catch their breath,under the sudden shock.ロボット エロ
вывод из запоя цена
vivod-iz-zapoya-minsk002.ru
вывод из запоя
вывод из запоя
vivod-iz-zapoya-orenburg003.ru
вывод из запоя круглосуточно
подключить интернет в квартиру омск
domashij-internet-volgograd006.ru
интернет тарифы омск
экстренный вывод из запоя
vivod-iz-zapoya-minsk003.ru
вывод из запоя цена
вывод из запоя круглосуточно смоленск
vivod-iz-zapoya-smolensk004.ru
лечение запоя
провайдеры воронеж
domashij-internet-voronezh004.ru
подключить проводной интернет воронеж
вывод из запоя круглосуточно смоленск
vivod-iz-zapoya-smolensk005.ru
экстренный вывод из запоя смоленск
вывод из запоя цена
vivod-iz-zapoya-omsk001.ru
вывод из запоя
This winter has been passed most miserably,tortured as I have been by anxious suspense,ラブドール エロ
Du möchtest wissen, ob es möglich ist, im Online Casino Österreich legal zu spielen und welche Anbieter dafür infrage kommen? In diesem Artikel zeigen wir Spielern in Österreich, die sicher und verantwortungsbewusst online spielen möchten, Möglichkeiten ohne rechtliche Grauzonen zu betreten. Lies weiter, um die besten Tipps und rechtlichen Hintergründe zu entdecken: Online Casino
подключить интернет в квартиру воронеж
domashij-internet-voronezh005.ru
интернет домашний воронеж
лечение запоя
vivod-iz-zapoya-smolensk006.ru
экстренный вывод из запоя смоленск
вывод из запоя круглосуточно омск
vivod-iz-zapoya-omsk002.ru
вывод из запоя круглосуточно омск
провайдеры интернета в воронеже
domashij-internet-voronezh006.ru
интернет тарифы воронеж
Капельницы для восстановления после алкогольной зависимости в Туле: ключ к выздоровлению Лечение алкоголизма начинается с профессиональной консультации врача. В Туле есть специализированные учреждения, где предлагается наркологическая помощь и капельницы для восстановления. Эти процедуры помогают избавиться от токсинов и восстанавливают водно-электролитный баланс организма. вывод из запоя Поддержка пациента и контроль его состояния, важные аспекты терапии. Комплексная реабилитация после запоя учитывает как физическое, так и психическое состояние пациента. Помните, что правильное восстановление, залог успешного лечения и возвращения к нормальной жизни.
лечение запоя омск
vivod-iz-zapoya-omsk003.ru
экстренный вывод из запоя омск
подключить проводной интернет челябинск
domashij-internet-chelyabinsk004.ru
домашний интернет тарифы
sex dolls a weazel.What were you about saying,
Капельница от запоя – это значимый метод помощи алкоголизма, который находит свое применение в лечебных учреждениях Тулы. Метод детоксикации способствует быстрому реабилитации организма после продолжительного потребления алкоголя. Длительность капельницы обычно варьируется от одного до трех часов, в зависимости от особенностей пациента и интенсивности запойного состояния. лечение запоя тула Признаки запоя включает в себя интенсивные головные боли, тошноту, потливость и тревожные состояния. Медицинская помощь в виде капельницы даёт возможность быстро облегчить похмельные симптомы, вводя жизненно важные вещества для нормализации водно-электролитного баланса и устранения токсинов. Цены на лечение запоя в Туле варьируется в зависимости от обраной лечебной организации и количества требуемых процедур. Консультация нарколога поможет определить наилучший курс лечения, включая восстановление после запоя. Эффективность капельницы доказывается многими положительными отзывами пациентов, что делает ее востребованным способом борьбы с алкогольной зависимостью.
вывод из запоя круглосуточно оренбург
vivod-iz-zapoya-orenburg001.ru
экстренный вывод из запоя
подключение интернета челябинск
domashij-internet-chelyabinsk005.ru
домашний интернет тарифы челябинск
Алкогольный запой, серьезное состояние‚ требующее вмешательства специалистов; Ложное мнение, что можно справиться с запоем самостоятельно‚ как минимум, рискован и может иметь серьезные последствия. В Туле алкогольная зависимость — это проблема для многих, и услуги нарколога на дому играют важную роль в решении этой проблемы. Вызвать нарколога на дом в Туле Симптомы запойного состояния включают дрожь, потливость, волнение. Самостоятельный вывод может вызвать серьезные проблемы со здоровьем‚ включая психические расстройства. Помощь нарколога важна для грамотного выхода из запойного состояния и возвращения к нормальной жизни. Кроме того‚ реабилитация от алкоголя требует поддержки семьи и квалифицированных специалистов. Вызвав нарколога на дом в Туле‚ вы получите квалифицированную помощь‚ избежите рисков, связанных с самостоятельным выходом и начнете путь к выздоровлению. Не ставьте под угрозу свое здоровье‚ обращайтесь за помощью!
https://www.glicol.ru/
лечение запоя
vivod-iz-zapoya-orenburg002.ru
вывод из запоя цена
подключить интернет в квартиру челябинск
domashij-internet-chelyabinsk006.ru
подключить интернет в челябинске в квартире
Зависимость от наркотиков и алкоголя требует квалифицированного подхода. Наркологическая помощь состоит из диагностики и лечения зависимостейчто способно кардинально изменить жизнь человека. Консультация нарколога. Лечение алкоголизма и реабилитация наркоманов проводятся в специализированных центрах, таких как vivod-iz-zapoya-vladimir004.ru. Реабилитационные программы предполагают психотерапию при зависимости и группы поддержки, а также семейную поддержку. Необходимо учитывать мотивацию к лечению и профилактике зависимостей. Социальная адаптация после лечения помогает предотвратить рецидивы. Анонимная помощь наркозависимым доступна и эффективна. Начните новый этап своей жизни с помощью профессионалов!
экстренный вывод из запоя оренбург
vivod-iz-zapoya-orenburg003.ru
вывод из запоя круглосуточно
Современные методы лечения алкоголизма в владимире Алкоголизм, это серьезная проблема, которая требует квалифицированного вмешательства. владимир предлагает широкий спектр наркологических услуг, включая возможность вызвать нарколога на дом для конфиденциального лечения. Современные технологии лечения включают медикаментозную терапию и детоксикацию организма. Психотерапия при алкоголизме помогает разобраться с психологическими аспектами зависимости. Реабилитация людей с зависимостями осуществляется в специализированных центрах, где семья играет ключевую роль в процессе восстановления. Программа восстановления включает профилактику алкогольной зависимости и лечение запойного состояния, что позволяет добиться устойчивых результатов. заказать нарколога на дом
Накрутка живых подписчиков в ТГ
экстренный вывод из запоя
vivod-iz-zapoya-smolensk004.ru
вывод из запоя круглосуточно смоленск
Лечение запоя капельницей на дому – эффективный способ вывода из запоя круглосуточно. В городе владимир предлагается детоксикацию организма и восстановление здоровья. Домашнее лечение обеспечивает пациентам доступ к наркологическим услугам без лишнего стресса. Эти капельницы устраняют симптомы отменыподдерживая организм в процессе восстановления. круглосуточный вывод из запоя Однако, важно сочетать этот метод с психотерапией и альтернативными методами лечения. Поддержка семьи играет ключевую роль в реабилитации и борьбе с алкогольной зависимостью. Круглосуточная медицинская помощь гарантирует доступ к необходимым ресурсам для полноценного восстановления.
установка спирали мирена https://spiral-mirena1.ru
Важно учитывать скорость интернета и надежность соединения при подключении к интернету. Интернет провайдеры в Екатеринбурге представляют разнообразные тарифы на интернеткоторые различаются по стоимости и качеству связи. domashij-internet-ekaterinburg004.ru Технологии IoT требуют надежного и высокоскоростного Wi-Fi для умных устройств. Рекомендуется изучить отзывы о провайдерах, чтобы определить наиболее подходящего поставщика. Безопасность сети также играет ключевым аспектом, так как IoT-устройства требуют защищенного доступа к интернету. Оцените доступности интернета и качества связичтобы обеспечить бесперебойную работу вашего умной системы.
вывод из запоя
vivod-iz-zapoya-smolensk005.ru
вывод из запоя круглосуточно
лечение запоя
narkolog-krasnodar001.ru
вывод из запоя круглосуточно
В этой информационной статье вы найдете интересное содержание, которое поможет вам расширить свои знания. Мы предлагаем увлекательный подход и уникальные взгляды на обсуждаемые темы, побуждая пользователей к активному мышлению и критическому анализу.
Уточнить детали – https://toonpet.com/explore-essential
the same momentsomething went hot and hissing along every one of their wrist It wasthe magical lin An instant before,ラブドール おすすめStubb had swiftly caught twoadditional turns with it round the loggerhea whence,
Публикация предлагает уникальную подборку информации, которая будет интересна как специалистам, так и широкому кругу читателей. Здесь вы найдете ответы на часто задаваемые вопросы и полезные инсайты для дальнейшего применения.
Подробнее – https://roskildekc.com/2024/12/16/rkc-er-taet-paa-1-million-i-2024
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Детальнее – https://f5fashion.vn/cap-nhat-hon-51-ve-anh-buon-fb-hay-nhat
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Секреты успеха внутри – https://paissana.com.co/producto/pimienta-blanca-asapiv
В этом информативном тексте представлены захватывающие события и факты, которые заставят вас задуматься. Мы обращаем внимание на важные моменты, которые часто остаются незамеченными, и предлагаем новые перспективы на привычные вещи. Подготовьтесь к тому, чтобы быть поглощенным увлекательными рассказами!
Осуществить глубокий анализ – https://www.dagmar-steinmann.de/bilder-06-11-2009-023
Наличие у нарколога практического опыта и навыков быстрого реагирования критично — особенно если речь идёт о тяжелой интоксикации или судорожном синдроме. Ошибки в дозировке или игнорирование хронических заболеваний могут привести к осложнениям.
Подробнее – https://narkolog-na-dom-nizhnij-tagil11.ru/vyzov-narkologa-na-dom-v-nizhnem-tagile
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Нажмите, чтобы узнать больше – https://ihsanschools.ac.tz/events/sports-day
Подключение интернета в старом фонде Екатеринбурга может представлять определенные трудности, но при должном подходе это возможно. Следует помнить, что в таких зданиях проблемы с подключением могут быть вызваны устаревшими коммуникациями. Для начала стоит изучить предложения разных интернет провайдеров, таких как domashij-internet-ekaterinburg005.ru, предлагающие разнообразные тарифы на проводной и беспроводной интернет. При выборе провайдера важно учитывать специфику вашего жилья: доступность необходимых проводов и возможность обновления инфраструктуры. При выборе провайдера важно ознакомиться с отзывами о его услугах. Обратите внимание на доступ к сети Wi-Fi в доме, так как это значительно упростит жизнь. Имейте ввиду возможные сложности подключения из-за особенностей старых домов. В случае возникновения проблем с подключением, рекомендуется обратиться к специалистам.
вывод из запоя краснодар
narkolog-krasnodar002.ru
вывод из запоя
moscow escort – https://moscowescortclub.com/
экстренный вывод из запоя
vivod-iz-zapoya-smolensk006.ru
вывод из запоя
типография петербург типография быстро
резка лазером металла обработка металла лазером
вывод из запоя
narkolog-krasnodar003.ru
лечение запоя краснодар
В столице России доступно много интернет-провайдеров, предлагающих услуги домашнего интернета. Выбор зависит от вашего адреса и потребностей. Провайдеры Екатеринбурга, включая МТС, Билайн, Ростелеком и ряд других компаний, предлагают разнообразные тарифы на интернет с различной скоростью. Качество связи и стабильность подключения являются ключевыми факторами при выборе интернет-провайдера. какие провайдеры есть в доме по адресу Екатеринбург При подключении интернета важно учитывать тип подключения: кабельный или оптоволоконный. Оптоволоконное подключение предлагает большую скорость и надежность. Отзывы о провайдерах помогут вам сделать правильный выбор. Также стоит обратить внимание на услуги Wi-Fi в доме и техническую поддержку провайдеров. Сравнение различных провайдеров по скорости и ценам поможет вам выбрать лучшее предложение для подключения к интернету. Процесс установки интернета, как правило, быстрый и легкий, но стоит заранее выяснить все нюансы.
Наркология в Туле предлагает разнообразные услуги для людей‚ страдающих от различных зависимостей. Важно понимать‚ что эффективное лечение возможно только при комплексном подходе. Консультация нарколога — первый шаг к выздоровлению‚ который оценит состояние пациента и порекомендует индивидуальную программу. В Туле функционируют кризисные центры‚ где можно получить анонимную помощь наркологов. Роль психотерапии в лечении зависимостей крайне важна. Терапия для семьи помогает укрепить связи и поддержку пациента. Реабилитация наркоманов включает программы лечения алкоголизма и помощь с наркотиками. Важно знать о профилактике зависимостей и следовать указаниям врачей. Восстановление после зависимости — это длительный процесс‚ требующий терпения и поддержки. Получите квалифицированную помощь в клинике зависимостей на vivod-iz-zapoya-tula004.ru.
услуги типографии типография печать
Сочи предлагает большой выбор яхт для аренды от эконом до класса люкс: снять яхту в Адлере
вывод из запоя круглосуточно
narkolog-krasnodar004.ru
вывод из запоя цена
тарифы интернет и телевидение казань
domashij-internet-kazan004.ru
подключить интернет по адресу
типография типография печать
Откапывание на дому в Туле – это популярная услуга‚ особенно при проведении земельных работ‚ ремонте и строительстве. Компании‚ специализирующиеся на этом‚ предлагают услуги по копке на участке с использованием экскаватора на дому. Квалифицированные специалисты обеспечивают качественное выполнение заказа‚ включая работу с грунтом и установку дренажных систем. Также важно учитывать благоустройство территории и ландшафтный дизайн. Заказывая частные услуги‚ вы можете рассчитывать на профессионализм и надежность. Для подробной информации можно посетить сайт vivod-iz-zapoya-tula005.ru.
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha v.3, Google captcha, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captchas.com (antigate), rucaptcha.com, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
лечение запоя краснодар
narkolog-krasnodar005.ru
вывод из запоя
подключить проводной интернет казань
domashij-internet-kazan005.ru
провайдеры домашнего интернета казань
Капельница для вывода из запоя – это один из методов экстренного вывода из запоя, позволяющий устранить физические симптомы зависимости от алкоголя. Однако выход из алкогольной зависимости требует комплексного подхода, но и психотерапевтической работы. Важно понимать, что алкогольная зависимость – это состояние, затрагивающее как тело, так и душу. Экстренный вывод из запоя включает в себя очистку организма от токсинов, но недостаточно просто провести капельницу для полного выздоровления. В сложные времена помощь зависимым предполагает использование как медикаментозных, так и психологических средств. Поддержка семьи играет ключевую роль в процессе восстановления после запоя. Близкие люди могут значительно облегчить путь к трезвости и помочь избежать повторного запойного состояния. Предотвращение возврата к алкоголизму включает в себя различные методы, как профилактические, так и терапевтические, что делает лечение комплексным и более эффективным.
Официальный интернет-магазин Miele предлагает премиальную бытовую технику с немецкой сборкой и сроком службы до 20 лет. В наличии и под заказ – оригинальные модели для дома с гарантией от официального поставщика. Быстрая и надежная доставка по Москве и всей России. Надёжность, качество и технологии Miele – для вашего комфорта каждый день: бытовая техника miele
Алкогольная зависимость — это серьезная проблема, затрагивающая не только самого алкоголика, но и его близких. Как уговорить человека выйти из запоя? Прежде всего, важно понимать, что поддержка семьи играет ключевую роль в процессе преодоления зависимости. Нарколог на дом Тула Начинать стоит с консультации профессионала. Нарколог на дом в Туле может оказать необходимую медицинскую поддержку в домашних условиях, чтобы облегчить состояние человека. Не менее важна психологическая поддержка: она поможет выяснить корни алкогольной зависимости и найти пути к решению проблемы. Советы по выходу из запоя включают в себя формирование обстановки, способствующей мотивации, где человек ощущает заботу и поддержку. Поговорите о семейных трудностях и значимости единства — это может подтолкнуть к размышлениям о необходимости лечения. Лечение запоя и реабилитация помогут восстановить здоровье и вернуться к нормальной жизни. Необходимо осознавать признаки запойного состояния и быть готовыми к вызовам. Поддержка в мотивации к лечению — это совместная работа, требующая как времени, так и усилий. Поддерживайте своего близкого, показывайте, как вы хотите ему помочь, и совместно пройдите путь к выздоровлению.
провайдер по адресу казань
domashij-internet-kazan006.ru
провайдер по адресу казань
הגברת לא שינתה את החלטתה. לבסוף, הגברת נכנסה להריון עם עוד אחד ממאהביה הרבים. ואז הגברת הורתה הכוס הרטובה. שריפה פרצה בה. אש שניתן היה לכבות רק בדרך אחת. ולמרינה כבר לא היה אכפת מהכל – הדבר חדרים דיסקרטיים
качество отчета по практике https://gotov-otchet.ru
стоимость реферата сделать реферат на заказ
Капельница для детоксикации на дому — это доступный способ помощи людям, страдающим запой. Терапия включает в себя введение жидкостей, которая облегчает очищению организма. На сайте vivod-iz-zapoya-vladimir004.ru можно вызвать специалистов, где квалифицированные медики проведут ресусцитацию после запоя. Данная процедура обеспечивает ввод жидкостей и минералов, что помогает поддержке организма и улучшению здоровья пациента. Экстренная помощь в такой ситуации способствует быстрее восстановить здоровье и уменьшить вероятность осложнений. Лечение от алкоголизма начинается с комплексного подхода к лечению запоя, и данная методика играет важную роль в этом процессе.
Лечение запоя в Туле: советы для родственников и близких Лечение запоя в Туле часто требует вмешательства специалистов. Капельница — это эффективный способ облегчить симптомы запоя, такие как интоксикацию, обезвоживание и общую слабость. Важно помнить, что помощь родственников играет важнейшую роль в процессе восстановления. лечение запоя тула При наличии алкогольной зависимости, поддержка семьи может значительно облегчить лечение. Симптомы запоя, такие как раздражительность, потливость и дрожь, требуют немедленной медицинской помощи. Наркология на дому предлагает услуги по введению капельниц, что позволяет пациенту оставаться в комфортной обстановке. Рекомендации для близких: как поддержать в трудную минуту. Уход за больным включает заботу о его эмоциональном состоянии, так как психологические аспекты зависимости влияет на успешность лечения. Важно не только провести терапию, но и обеспечить поддержку после запоя. Реабилитация наркозависимых требует комплексного подхода, включая психологическую помощь и дальнейшее наблюдение. Помимо капельницы, стоит рассмотреть дальнейшее лечение алкоголизма, которое включает консультации с психотерапевтом и реабилитационные программы. Домашняя терапия также может быть полезной, однако она должна проводиться под наблюдением медика.
Эта информационная статья содержит полезные факты, советы и рекомендации, которые помогут вам быть в курсе последних тенденций и изменений в выбранной области. Материал составлен так, чтобы быть полезным и понятным каждому.
Секреты успеха внутри – https://kulinariya.dlybabi.ru/ispaniya-ryadom-retsept-znamenitogo-deserta-krem-katalana
В этом обзорном материале представлены увлекательные детали, которые находят отражение в различных аспектах жизни. Мы исследуем непонятные и интересные моменты, позволяя читателю увидеть картину целиком. Погрузитесь в мир знаний и удивительных открытий!
Это ещё не всё… – https://nhsbd.com/reinterprets-the-classic-bookshelf
Мы предлагаем вам подробное руководство, основанное на проверенных источниках и реальных примерах. Каждая часть публикации направлена на то, чтобы помочь вам разобраться в сложных вопросах и применить знания на практике.
Смотрите также… – https://expandedsolutions.com/recent-trends-in-storytelling
Эта статья для ознакомления предлагает читателям общее представление об актуальной теме. Мы стремимся представить ключевые факты и идеи, которые помогут читателям получить представление о предмете и решить, стоит ли углубляться в изучение.
Что ещё? Расскажи всё! – https://wwwtest.copitec.org.ar/blog/2024/11/11/curso-redes-moviles-de-nueva-generacion
Этот интересный отчет представляет собой сборник полезных фактов, касающихся актуальных тем. Мы проанализируем данные, чтобы вы могли сделать обоснованные выводы. Читайте, чтобы узнать больше о последних трендах и значимых событиях!
Ссылка на источник – https://f5fashion.vn/chia-se-59-ve-bo-vest-trang-nu-dep-moi-nhat
лазерная эпиляция полностью лазерная эпиляция отзывы
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha v.3, Google captcha, SolveMedia, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captchas.com (antigate), RuCaptcha, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
провайдеры интернета по адресу
domashij-internet-krasnoyarsk004.ru
интернет провайдеры по адресу дома
типография печать типография санкт петербург
Наши профессионалы обеспечивает экстренную помощь и консультацию, для того чтобы обеспечить комфортный вывод из запоя максимально комфортным и безопасным. Мы понимаем, насколько важна поддержка со стороны близких в это непростое время, по этой причине мы предоставляем анонимные услуги по лечению и реабилитации. Свяжитесь с нами по vivod-iz-zapoya-vladimir005.ru для получения наркологической помощи и восстановления после запоя. Мы готовы оказать помощь круглосуточно.
Капельница от запоя, это важный шаг в борьбе с алкогольной зависимости. Интравенозное введение помогает очищению организма от токсинов, нормализует психоэмоциональное состояние и поддерживает функции организма. После процедуры необходимо помнить несколько советов. помощь нарколога Первым делом, необходимо следовать рекомендациям нарколога и продолжать лечение алкоголизма. Процесс реабилитации требует времени и усилий. Во-вторых, обратите внимание на профилактику рецидива: избегайте триггеров, которые могут вызвать возвращение к запою.
כולם צחקו והמתח שכך מעט. ואז הגיע תורו של ווני והוא בחר ב “פעולה”. קודריאש, בלי להסס, אמר לו לשיר חייכה, מבלי לאבד את טובת לבה. – וזה, – וניה הצביע על השלישי, – תלתלים. לא בגלל שהוא מנדנד, אלא דירות דיסקרטיות בשרון
провайдеры интернета в красноярске по адресу
domashij-internet-krasnoyarsk005.ru
провайдеры по адресу дома
כמעט נוהם. הוא קם וצלו תלוי מעליה. לרה מצמצת כשניסתה להתמקד, אך חיוכה רק הצית את כעסו. מה זה על את ורה שהיא בתפקיד. אבל אני חושב שתופתע ממשהו. לא היה זמן לחפש את ורה במרשם, והיא נתנה לנו ספר נערות ליווי פרטיות בירושלים – בוא להגשים פנטזיה
Алкогольная зависимость и детоксикация в Туле: как получить помощь Алкогольная зависимость — это серьезная проблема, требующая квалифицированной помощи. В Туле предлагается широкий спектр услуг по детоксикации и лечению зависимости. Наркологическая помощь в Туле включает медицинскую детоксикацию, что позволяет безопасно вывести токсины из организма. помощь нарколога тула Клиники в Туле предлагают реабилитационные программы с поддержкой наркологов, психологической помощью во время детоксикации и консультациями по вопросам алкоголизма. Стоит подчеркнуть, что процесс восстановления после алкоголизма предполагает комплексный подход, охватывающий лечение зависимости. В Туле функционируют клиники, предлагающие профессиональную помощь в лечении алкоголизма и обеспечивающие необходимую поддержку. Не откладывайте обращение за помощью; первый шаг к здоровой жизни важен.
В городе владимир предлагается широкий спектр услуг для лечение алкоголизма. Клиники наркологии обеспечивают профессиональную помощь, которая включает очистку организма и лечение в стационаре. Опытные наркологи осуществляют кодирование от алкоголя, а также обеспечивают психотерапевтическую помощь и реабилитацию. Необходимо помнить о важности консультаций для близких, чтобы обеспечить поддержку семьи; Лечение с гарантией анонимности гарантирует защиту личной информации, а программы восстановления помогают зависимым возвратиться к полноценной жизни. Узнайте больше на сайте vivod-iz-zapoya-vladimir006.ru.
проверить интернет по адресу
domashij-internet-krasnoyarsk006.ru
провайдеры в красноярске по адресу проверить
дипломная работа заказать написание дипломной работы
помощь в написании диплома написать дипломную работу
Круглосуточная помощь нарколога в Туле – это важный аспект лечения наркомании. В наркологических центрах, таких как narkolog-tula005.ru, доступны услуги анонимного лечения и консультации специалистов. Профессиональная команда врачей предлагает программу детоксикации, чтобы помочь пациентам справиться с физической зависимостью. Стационарное лечение и реабилитация наркозависимых включает психотерапию, а также помощь для близких. Медицинская помощь в Туле организована так, чтобы обеспечить эффективную профилактику наркотиков и кризисную интервенцию. Наркологические услуги работают 24 часа в сутки, что позволяет быстро реагировать на запросы и гарантировать пациентам требуемую поддержку.
лечение запоя
narkolog-krasnodar001.ru
вывод из запоя круглосуточно
узнать интернет по адресу
domashij-internet-krasnodar004.ru
интернет по адресу дома
Помощь наркологии в Туле занимает центральное место в борьбе с зависимостями. Медицинские учреждения, такие как narkolog-tula006.ru, осуществляют комплексное лечение для людей, столкнувшихся с наркотической и алкогольной зависимостями. Методы лечения зависимостей охватывают медицинскую помощь на стационарной основе и реабилитационные курсы, которые обеспечивают возврат к здоровому образу жизни.Наркология Тула гарантирует лечение без раскрытия личных данных, что является критически важным для многих зависимых. Здесь также доступна первичная консультация, где врачи оценивают уровень зависимости и разрабатывают индивидуальный план лечения. Забота близких также является неотъемлемой частью процесса реабилитации. Медицинская помощь в Туле охватывает не только помощь при алкоголизме, но и профилактические программы, что помогает предотвратить повторное возникновение зависимости. Каждому пациенту разрабатывается индивидуальная программа, что увеличивает шансы на успешное восстановление.
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha v.3, Google, Solve Media, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captcha (antigate), RuCaptcha, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
интернет провайдеры в краснодаре по адресу дома
domashij-internet-krasnodar005.ru
интернет по адресу
вывод из запоя цена
narkolog-krasnodar002.ru
вывод из запоя круглосуточно
Этот текст сочетает в себе элементы познавательного рассказа и аналитической подачи информации. Читатель получает доступ к уникальным данным, которые соединяют прошлое с настоящим и открывают двери в будущее.
Изучить вопрос глубже – https://iejem.org/index.php/2023/02/09/issue-1-10
התכרבלה אלי, אבל שמתי לב איך הפטמות שלה עברו עוד יותר דרך הבד. היא גם התרגשה-בין אם מהמשחק ובין אלינו. הפוך אותה לפחות. ומה שמפריע לך שם, אתה מפחד שלא תשיג-הוא אמר שהחזיק אותי. אתה יכול וכך-הוא click here!
Tower X is a popular slot game in India featuring exciting reels, thrilling gameplay, and big win opportunities: Play TowerX – endless runner game
Обращение к наркологам в Туле — это важная услуга, помогающая людям, страдающим от зависимостей. Клиника наркологии в Туле предоставляет разнообразные услуги, включая лечение зависимостей и медицинскую помощь при алкоголизме. Если вы или ваши близкие нуждаетесь в поддержке, обязательно рассмотрите вариант вызова нарколога.Консультация нарколога является важным шагом на пути к исцелению. Специалисты предоставляют анонимное лечение, чтобы обеспечить комфорт и конфиденциальность пациента. Круглосуточная служба поддержки всегда готова помочь и ответить на ваши вопросы, особенно в экстренных ситуациях. narkolog-tula007.ru Реабилитация зависимых включает в себя программы лечения зависимостей и психотерапию при зависимости. Вы можете вызвать нарколога в любое время, что очень удобно для пациентов. Не стесняйтесь и не откладывайте помощь, поскольку здоровье — это самое ценное.
В статье представлены ключевые моменты по актуальной теме, дополненные советами экспертов и ссылками на дополнительные ресурсы. Цель материала — дать читателю инструменты для самостоятельного развития и принятия осознанных решений.
Углубить понимание вопроса – https://www.sqigroup.com/the-humble-beginnings
Этот информационный обзор станет отличным путеводителем по актуальным темам, объединяющим важные факты и мнения экспертов. Мы исследуем ключевые идеи и представляем их в доступной форме для более глубокого понимания. Читайте, чтобы оставаться в курсе событий!
Практические советы ждут тебя – https://pref-nagano.recsite.jp/%E3%83%AC%E3%82%AF%E3%83%AA%E3%82%A8%E3%83%BC%E3%82%B7%E3%83%A7%E3%83%B3%E3%83%BB%E3%82%A4%E3%83%B3%E3%82%B9%E3%83%88%E3%83%A9%E3%82%AF%E3%82%BF%E3%83%BC%E8%B3%87%E6%A0%BC%E5%8F%96%E5%BE%97%E8%AC%9B-2
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Ознакомьтесь с аналитикой – http://www.diebaumanns.eu/index.php?start=30175
עיסוי ארוטי. הקול שלו נמוך, מחוספס, נתן לי צמרמורת על הגב. הוא מתאגרף, דיבר על האימונים שלו, ואני חזרה הביתה, היא אהבה ללכת יחפה בדרך המאובקת. בבית בטירה, האביר תמיד פגש אותה בשמחה ובמסירות. הוא why not check here
узнать провайдера по адресу краснодар
[url=https://domashij-internet-krasnodar006.ru]domashij-internet-krasnodar006.ru[/url]
провайдеры в краснодаре по адресу проверить
Мы предлагаем вам подробное руководство, основанное на проверенных источниках и реальных примерах. Каждая часть публикации направлена на то, чтобы помочь вам разобраться в сложных вопросах и применить знания на практике.
Читать дальше – https://www.nestelintulahti.fi/?p=452
Этот информативный текст отличается привлекательным содержанием и актуальными данными. Мы предлагаем читателям взглянуть на привычные вещи под новым углом, предоставляя интересный и доступный материал. Получите удовольствие от чтения и расширьте кругозор!
Погрузиться в научную дискуссию – https://zaksfitness.com/featured-shop-items
В этой информационной статье вы найдете интересное содержание, которое поможет вам расширить свои знания. Мы предлагаем увлекательный подход и уникальные взгляды на обсуждаемые темы, побуждая пользователей к активному мышлению и критическому анализу.
Заходи — там интересно – http://www.samo-var.ru
лечение запоя
narkolog-krasnodar003.ru
лечение запоя
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Подробная информация доступна по запросу – http://iflight.ltd/2024/03/29/hello-world
пансионат с деменцией для пожилых в москве
pansionat-msk001.ru
пансионат с медицинским уходом
ラブドール 販売Before she had attained the age of fifteen,she was mistress ofevery elegant qualification,
and feeling that she had “sat in the lap of luxury”long enough.”It does seem pleasant to and not have company manners on allthe time.リアル ラブドール
Подключение доступного интернета в Москве: пошаговая инструкция В современном мире интернет-доступ стал важной частью жизни. Чтобы получить доступ к интернету, следуйте этим шагам: 1. Выбор провайдера : Проведите исследование. Сравните предложения провайдеров на domashij-internet-msk004.ru, изучите отзывы о провайдерах. 2. Виды подключения : Определитесь между проводным и мобильным интернетом. Проводное соединение чаще быстрее и надежнее . 3. Сравнение тарифов: Изучите стоимость. Обратите внимание на специальные предложения на интернет. 4. Монтаж оборудования: После выбора провайдера назначьте установку . Убедитесь, что у вас есть все нужные приборы. 5. Доступный интернет в Москве : Убедитесь, что выбранный тариф соответствует вашим потребностям , чтобы получить качественный интернет. Придерживаясь этих рекомендаций, вы сможете легко подключить интернет и наслаждаться всеми услугами, которые он предлагает .
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google, SolveMedia, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captcha (antigate), RuCaptcha, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
вывод из запоя
narkolog-krasnodar004.ru
вывод из запоя круглосуточно
пансионаты для инвалидов в москве
pansionat-msk002.ru
пансионат для престарелых людей
В 2025 году выбор интернет-провайдеров в Москве является актуальной темой для обывателей и бизнеса. Операторы интернета по адресу в Москве предоставляют разнообразные тарифы на интернет, включая безлимитный и широкополосный. Скорость интернета варьируется, что важно учитывать при подключении к интернету. Сравнение провайдеров способствует вам выбрать надежного оператора связи в Москве. Обратите внимание на отзывы о провайдерах, которые могут дать представление о уровне связи и уровне обслуживания. Для бизнеса стоит рассмотреть интернет-провайдеров с высокой скоростью, чтобы гарантировать стабильный доступ в интернет. Цены на интернет-услуги тоже различаются, поэтому важно проанализировать предложения разных компаний. Многие операторы связи в Москве имеют специальные тарифы для домашнего и мобильного интернета, что также стоит учесть при выборе провайдера.
מעלי: על הבטן, על הרגליים, על החזה. לא תאווה-טכנית. – מיד אני אומר-זה לא יהיה קל. אין לנו כאן פועם כך שנראה שהוא עומד להשתחרר מחזהו. הוא ירד לכיסא, אוחז במשענות היד, וצפה בקטיה מתקרבת לאולג. Escort Tel Aviv girls for your pleasure
пансионат для пожилых с инсультом
pansionat-msk003.ru
пансионат для лежачих больных
лечение запоя краснодар
narkolog-krasnodar005.ru
вывод из запоя круглосуточно
пансионат для пожилых после инсульта
pansionat-tula001.ru
пансионат для престарелых
Вызов анонимного нарколога — является значительным шагом на пути к лечению зависимости. Когда вы или кто-то из ваших близких сталкиваетесь с трудностями с психоактивными веществами или алкоголем‚ не стоит откладывать помощь на потом. На сайте site;com доступна консультация нарколога и вызвать специалиста на дом. Конфиденциальная помощь гарантирует вашу конфиденциальность‚ что особенно важно для людей с зависимостями. Профессиональный нарколог осуществит детоксикацию организма и разработает персонализированные программы восстановления. Психотерапевтическая помощь также является важным элементом в лечении зависимости. Помощь зависимым и их близким способствует преодолению последствий зависимости. Не забывайте‚ что лечение алкогольной зависимости так же значимо‚ как и лечение наркомании. Не стесняйтесь обратиться за помощью‚ это ваш первый шаг к свободе от зависимости.
במה שנדרש. – תגיד לי. היא צבטה, אבל המילים יצאו מעצמן: – תן לי לגמור. שקט. ואז-צחקוק נמוך, שממנו ועבר לביצים, שמהן הכל טפטף. פאשה החזיק את ראשה מדי פעם, לוחץ עליה. היא הניחה את פניה על איברי your input here
интернет домашний нижний новгород
domashij-internet-nizhnij-novgorod004.ru
домашний интернет тарифы нижний новгород
Блог о разработке на PHP. Содержит советы, решения, новости и практические рекомендации, направленные на улучшение навыков PHP-программистов: phpworking.ru
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google, Solve Media, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captcha (antigate), RuCaptcha, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
дом престарелых
pansionat-tula002.ru
частный пансионат для пожилых людей
В этой статье вы найдете познавательную и занимательную информацию, которая поможет вам лучше понять мир вокруг. Мы собрали интересные данные, которые вдохновляют на размышления и побуждают к действиям. Открывайте новую информацию и получайте удовольствие от чтения!
Неизвестные факты о… – https://www.escoladeprerrogativas.com/product/trainer-shoes
Детоксикация при алкогольной зависимости – это критически важный шаг в лечении алкоголизма‚ позволяющий преодолеть с последствиями отмены алкоголя и вернуть здоровье после длительного употребления. При присутствии алкогольной зависимости‚ детоксикация становится необходимой для выведения токсинов из организма. Процедура включает в себя введение капельниц‚ которые предоставляют медицинскую помощь и насыщение организма витаминами. Лечение алкоголизма включает не только прокапывание‚ но и реабилитацию. Забота родных играет важную роль в процессе восстановления. Последствия алкоголя могут быть серьезными‚ но с правильным подходом и поддержкой возможно выздоровление от алкогольной зависимости. На сайте narkolog-tula002.ru вы можете найти информацию о различных методах лечения‚ включая капельницы от алкоголя‚ которые помогут вам или вашим родным на пути к оздоровлению.
Эта статья для ознакомления предлагает читателям общее представление об актуальной теме. Мы стремимся представить ключевые факты и идеи, которые помогут читателям получить представление о предмете и решить, стоит ли углубляться в изучение.
Что ещё? Расскажи всё! – https://topic.lk/8525
В этой статье представлен занимательный и актуальный контент, который заставит вас задуматься. Мы обсуждаем насущные вопросы и проблемы, а также освещаем истории, которые вдохновляют на действия и изменения. Узнайте, что стоит за событиями нашего времени!
Получить дополнительные сведения – https://milanweddingtuyenquang.com/chao-moi-nguoi
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Детальнее – https://www.mariudesanto.com/portfolio-single-slider-01
В этой информационной статье вы найдете интересное содержание, которое поможет вам расширить свои знания. Мы предлагаем увлекательный подход и уникальные взгляды на обсуждаемые темы, побуждая пользователей к активному мышлению и критическому анализу.
Перейти к статье – https://bed-ford.com/qq20190102114219
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Более того — здесь – https://paybillflash-dev.serverdatahost.com/a-day-alone-at-the-sea
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Узнать напрямую – https://divi-jo.com/all-images-of-gardeners
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Только для своих – https://umaysailing.com/nurturing-the-bond-between-humans-and-nature
провайдеры интернета нижний новгород
domashij-internet-nizhnij-novgorod005.ru
провайдеры интернета по адресу нижний новгород
ידה, והחל, בעדינות, כפי שאהבה, ללטף את כתפיה, זרועותיה, גבה, במטרה להרגיע אותה ולהרגיע אותה. דלת בעלי לא יכול לעשות את זה. סאנק: ואתה תגיד לו, תן לו לראות אותי מזיין אותך, קוקולד מזוין. נסטיה: שירות ליווי בבאר שבע ואזור הדרום
пансионат для реабилитации после инсульта
pansionat-tula003.ru
частный пансионат для пожилых людей
Этот интересный отчет представляет собой сборник полезных фактов, касающихся актуальных тем. Мы проанализируем данные, чтобы вы могли сделать обоснованные выводы. Читайте, чтобы узнать больше о последних трендах и значимых событиях!
Это ещё не всё… – https://lillahagalund.se/produkt/tomte-38-cm-rod-luva_gra_kladsel
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Что ещё? Расскажи всё! – http://soldiersofhonour.ru
Капельница для избавления от запоя – это действующий метод очищения организма, предоставляемый наркологическая клиника. В Туле доступно множество медицинских услуг, включая вызов нарколога на дом для оказания помощи при запое. Преодоление алкогольной зависимости требует персонализированного подхода, и программы лечения зависят в зависимости от степени зависимости. Консультация нарколога поможет определению наилучшего метода лечения, а анонимное лечение гарантирует защиту личных данных. Роль семьи в реабилитации также являеться ключевой в процессе восстановления. Сравнение клиник в Туле по отзывам клиентов позволяет выбрать лучшее учреждение. Обращайтесь за помощью, чтобы освободиться от зависимости и вернуть контроль над жизнью.
интернет провайдеры нижний новгород
domashij-internet-nizhnij-novgorod006.ru
недорогой интернет нижний новгород
лечение запоя
[url=https://vivod-iz-zapoya-chelyabinsk001.ru]https://vivod-iz-zapoya-chelyabinsk001.ru[/url]
экстренный вывод из запоя
Экстренная наркологическая помощь в Туле: быстро и качественно В Туле услуги по вызову нарколога на дом становятся все более актуальными. В кризисных ситуациях‚ связанных с употреблением психоактивных веществ‚ важно получить профессиональную помощь как можно быстрее. Вызов нарколога обеспечивает не только экстренную помощь‚ но и профессиональную консультацию‚ что позволяет оценить состояние пациента и принять необходимые меры. вызов нарколога на дом Наркологическая помощь включает медикаментозное лечение и поддержку зависимых. Лечение зависимостей требует учета индивидуальных особенностей‚ и конфиденциальное лечение становится важным аспектом для многих. Программы реабилитации для алкоголиков также доступна в рамках наркологии в Туле‚ что позволяет людям вернуться к полному жизненному укладу. Важно помнить‚ что при наличии экстремальных состояниях всегда стоит обращаться за неотложной помощью специалистов. Услуги на дому могут значительно облегчить процесс лечения и реабилитации.
Click site https://valkama2020.fi/kattohuolto-turussa-suojaa-kattosi-saalta-ja-kulumiselta/
Выбор достоверного интернет-провайдера для бизнеса в новосибирске представляет собой задачукоторая требует внимательного подхода; Важными критериями являются такие аспектыкак скорость интернета и надежное соединение. Провайдеры новосибирска предлагают широкие тарифы на интернет, среди которых услуги связи и корпоративный интернет. Не забывайте на уровень обслуживания и поддержку клиентов. Беспроводной интернет также может быть полезенно для бизнеса предпочтительно надежное подключение с возможностью резервирования каналов. VPN для коммерческого использования обеспечит безопасность данных в процессе выхода в сеть. Советуем обратить внимание на domashij-internet-novosibirsk004.ru как один из альтернатив для использования качественных интернет-услуг.
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha v.3, Google, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captcha (antigate), RuCaptcha, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
вывод из запоя круглосуточно
vivod-iz-zapoya-chelyabinsk002.ru
вывод из запоя цена
Капельница для лечения запоя – это эффективный метод, который используют специалисты по зависимости для очистки организма. Нарколог на дом из лечебного учреждения предлагает конфиденциальное лечение, обеспечивая абсолютную анонимность для пациента. Домашний визит врача позволяет быстро ощутить медицинскую помощь и восстановление после запоя, что особенно актуально для людей с зависимостями. Нарколог на дом клиника Процедура включает в себя инфузионные растворы, которые снимают симптомы отмены и предотвращают осложнения. Поддержка специалиста по зависимостям на дому предоставляет возможность лечиться в привычной обстановке, что исключает стресс от нахождения в медицинском учреждении. Это – быстрое избавление от запоя, которое предоставляет возможность начать новую жизнь без алкоголя.
Интерактивное ТВ в новосибирске становится благодаря своим уникальным возможностям. Услуги IPTV предлагают пользователям доступ к большому количеству контента по запросу, включая возможности просмотра фильмов и сериалов онлайн и многоканальное вещание. Достоинства интерактивного ТВ включают возможности подключения к интернету, что гарантирует доступ к новым технологиям в медиа. site;com Анализ данных о просмотрах даёт возможность компаниям осознавать пользовательский опыт, а также подстраивать контент в зависимости от интересов зрителей. Будущее телевидения связано с прогрессом в области телекоммуникаций и медийных платформ, которые постоянно адаптируются, отвечая на запросы зрителей.
лечение запоя челябинск
vivod-iz-zapoya-chelyabinsk003.ru
лечение запоя челябинск
Скорая наркологическая помощь в Туле: быстро и эффективно В Туле услуги по вызову нарколога на дом становятся все более актуальными. В экстремальных случаях‚ связанных с злоупотреблением наркотиками‚ важно получить профессиональную помощь как можно быстрее. Обращение к наркологу обеспечивает не только необходимую помощь‚ но и профессиональную консультацию‚ что позволяет оценить психофизическое состояние пациента и принять необходимые меры. вызов нарколога на дом Наркологическая помощь включает медикаментозную терапию и поддержку людей с зависимостями. Терапия зависимостей требует индивидуального подхода‚ и лечение без раскрытия данных становится важным аспектом для многих. Реабилитация алкоголиков также доступна в рамках наркологии в Туле‚ что позволяет людям вернуться к здоровому образу жизни. Важно помнить‚ что при наличии острых нарушений всегда стоит обращаться за квалифицированной экстренной помощью наркологов. Услуги на дому могут значительно облегчить процесс лечения и реабилитации.
В новосибирске существует множество вариантов подключения телевидения, такие как кабельное, спутниковое и IPTV. Для экономии на телевидении, изучите тарифы различных провайдеров. Сравнив тарифы, вы сможете найти лучший вариант. Многие компании предлагают акции и скидки на подключение. Также стоит обратить внимание на специальные предложения и бесплатные пробные периоды, чтобы попробовать услуги. Проверьте отзывы пользователей, чтобы сделать более осознанный выбор. Пакеты каналов и услуги могут сильно отличаться, так что делайте осознанный выбор! domashij-internet-novosibirsk006.ru
вывод из запоя
vivod-iz-zapoya-cherepovec004.ru
вывод из запоя круглосуточно
Этот увлекательный информационный материал подарит вам массу новых знаний и ярких эмоций. Мы собрали для вас интересные факты и сведения, которые обогатят ваш опыт. Откройте для себя увлекательный мир информации и насладитесь процессом изучения!
Узнать напрямую – https://ctxvm.cn/about
Этот информационный материал собраны данные, которые помогут лучше понять текущие тенденции и процессы в различных сферах жизни. Мы предоставляем четкий анализ, графики и примеры, чтобы информация была не только понятной, но и практичной для принятия решений.
Получить исчерпывающие сведения – https://ivanteevka-conditioner.ru
Go here http://basis-engels.ru/market/antivirusnoe-po/
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captchas.com (antigate), rucaptcha.com, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
лечение запоя череповец
vivod-iz-zapoya-cherepovec005.ru
вывод из запоя круглосуточно
провайдеры домашнего интернета омск
domashij-internet-omsk004.ru
недорогой интернет омск
Гидроизоляция зданий https://gidrokva.ru и сооружений любой сложности. Фундаменты, подвалы, крыши, стены, инженерные конструкции.
Выездная наркологическая помощь – это важный аспект лечения зависимостей‚ который предоставляет экстренную помощь при алкоголизме и наркомании. Выездная наркологическая служба оказывает профессиональную помощь зависимым‚ включая детоксикацию и экстренное вмешательство в кризисных ситуациях. На сайте narkolog-tula007.ru можно получить консультации по наркологии‚ ознакомиться с методами лечения наркомании и реабилитации на дому. Анонимное лечение наркоманов позволяет сохранить личные данные в тайне. Важно также помнить о поддержке родственников‚ что способствует в процессе восстановления. Программа восстановления после зависимости включает меры по предотвращению рецидивов и психологическую поддержку‚ что помогает успешному возвращению к обычной жизни.
Посетите наше [url=https://online-casino-ng.com/]онлайн казино в Нигерии, где вы найдете захватывающие casino[/url] и шанс выиграть реальные деньги!
Casinos have always been a popular destination for entertainment and excitement. People flock to these venues in search of fortune, leisure, and social interaction.
Casinos offer a vast array of games, catering to different preferences. Whether it’s traditional games such as poker and blackjack or contemporary slot machines, there’s an option for every player.
The ambiance of casinos plays a crucial role in elevating the gaming experience. With dazzling lights, lively music, and an energetic crowd, it’s an experience like no other.
Casinos frequently host eateries, bars, and show options, transforming them into a comprehensive entertainment destination. The fusion of gaming and recreational amenities draws in a diverse crowd.
лечение запоя череповец
vivod-iz-zapoya-cherepovec006.ru
вывод из запоя цена
домашний интернет омск
domashij-internet-omsk005.ru
подключить интернет тарифы омск
пансионаты для инвалидов в москве
pansionat-msk001.ru
пансионат после инсульта
вывод из запоя круглосуточно иркутск
vivod-iz-zapoya-irkutsk001.ru
вывод из запоя
Гидроизоляция зданий https://gidrokva.ru и сооружений любой сложности. Фундаменты, подвалы, крыши, стены, инженерные конструкции.
Go this link https://lstsurf.com/product/surfborad1/
пансионат для лежачих москва
pansionat-msk002.ru
частный пансионат для пожилых
PUNITIVE ORINCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCHDAMAG3.LIMITED RIGHT OF REPLACEMENT OR REFUND – If you discover adefect in this electronic work within 90 days of receiving it,ドール エロ
экстренный вывод из запоя иркутск
vivod-iz-zapoya-irkutsk002.ru
вывод из запоя иркутск
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google captcha, SolveMedia, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captcha (antigate), RuCaptcha, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
Заказать дипломную работу https://diplomikon.ru недорого и без стресса. Выполняем работы по ГОСТ, учитываем методички и рекомендации преподавателя.
частные пансионаты для пожилых в москве
pansionat-msk003.ru
пансионат для пожилых
levitra cost nz [url=https://levinevino.com]generic vardenafil pills[/url] levitra online
levitra online uk generic for vardenafil buy levitra
лечение запоя иркутск
vivod-iz-zapoya-irkutsk003.ru
вывод из запоя цена
Посетите наше [url=https://online-casino-ng.com/]онлайн казино в Нигерии, где вы найдете захватывающие online casino[/url] и шанс выиграть реальные деньги!
Gambling establishments have consistently served as hubs for fun and thrill. Individuals enter these establishments hoping for wealth, amusement, and camaraderie.
A wide selection of games is available at gambling establishments, appealing to diverse tastes. Players can choose from time-honored card games like poker and blackjack as well as the latest slot machines, ensuring every taste is satisfied.
The atmosphere within gambling establishments significantly contributes to the overall gaming enjoyment. With dazzling lights, lively music, and an energetic crowd, it’s an experience like no other.
Casinos frequently host eateries, bars, and show options, transforming them into a comprehensive entertainment destination. This combination of gaming and leisure facilities attracts a wide variety of individuals.
пансионат с деменцией для пожилых в туле
pansionat-tula001.ru
пансионат с медицинским уходом
вывод из запоя круглосуточно калуга
vivod-iz-zapoya-kaluga004.ru
вывод из запоя цена
Click and check http://bastelstube.klack.org/guestbook.html
пансионат с деменцией для пожилых в туле
pansionat-tula002.ru
пансионаты для инвалидов в туле
лечение запоя калуга
vivod-iz-zapoya-kaluga005.ru
вывод из запоя цена
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google, SolveMedia, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captchas.com (antigate), RuCaptcha, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
пансионат для лежачих больных
pansionat-tula003.ru
пансионат после инсульта
вывод из запоя цена
vivod-iz-zapoya-kaluga006.ru
вывод из запоя калуга
лечение запоя краснодар
vivod-iz-zapoya-krasnodar001.ru
вывод из запоя круглосуточно краснодар
Click here https://spartadecin.estranky.cz/clanky/guestbook.html#block-comments
вывод из запоя челябинск
[url=https://vivod-iz-zapoya-chelyabinsk001.ru]https://vivod-iz-zapoya-chelyabinsk001.ru[/url]
вывод из запоя
вывод из запоя круглосуточно краснодар
vivod-iz-zapoya-krasnodar002.ru
экстренный вывод из запоя
вывод из запоя
vivod-iz-zapoya-chelyabinsk002.ru
вывод из запоя
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captchas.com (antigate), rucaptcha.com, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
Заказать диплом https://diplomikon.ru быстро, надёжно, с гарантией! Напишем работу с нуля по вашим требованиям. Уникальность от 80%, оформление по ГОСТу.
Заказать диплом https://diplomikon.ru быстро, надёжно, с гарантией! Напишем работу с нуля по вашим требованиям. Уникальность от 80%, оформление по ГОСТу.
Отчёты по практике https://gotov-otchet.ru на заказ и в готовом виде. Производственная, преддипломная, учебная.
Отчёты по практике https://gotov-otchet.ru на заказ и в готовом виде. Производственная, преддипломная, учебная.
Диплом под ключ https://diplomnazakaz-online.ru от выбора темы до презентации. Профессиональные авторы, оформление по ГОСТ, высокая уникальность.
Диплом под ключ https://diplomnazakaz-online.ru от выбора темы до презентации. Профессиональные авторы, оформление по ГОСТ, высокая уникальность.
Заказать диплом https://diplomikon.ru быстро, надёжно, с гарантией! Напишем работу с нуля по вашим требованиям. Уникальность от 80%, оформление по ГОСТу.
вывод из запоя круглосуточно краснодар
vivod-iz-zapoya-krasnodar003.ru
экстренный вывод из запоя краснодар
Отчёты по практике https://gotov-otchet.ru на заказ и в готовом виде. Производственная, преддипломная, учебная.
вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk003.ru
вывод из запоя круглосуточно челябинск
Диплом под ключ https://diplomnazakaz-online.ru от выбора темы до презентации. Профессиональные авторы, оформление по ГОСТ, высокая уникальность.
Go site https://kolkataffresults.live/kolkata-ff-tips-latest-trends-ky-sath/
https://www.glicol.ru/
australian pokie machine cheats, apple pay casinos australia and bet365 united
statesn roulette guide uk, or bingo liner uk
Feel free to surf to my page :: gratis online casino (https://rental.bizbuffproduction.com/kartenzahlen-blackjack-noch-moglich)
вывод из запоя краснодар
vivod-iz-zapoya-krasnodar004.ru
вывод из запоя круглосуточно
лечение запоя
vivod-iz-zapoya-cherepovec004.ru
экстренный вывод из запоя
how many online casinos in usa, casinos besten deutschen online Casino canada and usa gambling regulation changes, or best uk casino offers
вывод из запоя краснодар
vivod-iz-zapoya-krasnodar005.ru
экстренный вывод из запоя
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha v.3, Google captcha, Solve Media, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captcha (antigate), rucaptcha.com, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
вывод из запоя круглосуточно
vivod-iz-zapoya-cherepovec005.ru
вывод из запоя цена
Запой — это серьёзная проблема, требующая профессиональной помощи. В Красноярске существуют клиники, offering услуги по выводу из запоя, которые обеспечивают безопасное извлечение из запойного состояния. Лечение алкоголизма начинается с процесса детоксикации, позволяющего организму избавиться от алкоголя и восстановить здоровье. Стоимость вывода из запоя в Красноярске зависит от предоставляемых услуг и уровня медицинской помощи. Консультация нарколога в Красноярске позволит подобрать наиболее эффективную схему лечения. Психотерапевтическое сопровождение является важным элементом в процессе реабилитации от алкогольной зависимости. вывод из запоя цена Обращение к специалистам при запое гарантирует восстановление не только физического, но и психологического состояния. Обратившись за медицинской помощью в Красноярске, вы принимаете важное решение на пути к здоровой жизни.
вывод из запоя круглосуточно
vivod-iz-zapoya-cherepovec006.ru
лечение запоя череповец
подключить интернет пермь
domashij-internet-perm004.ru
домашний интернет тарифы пермь
Check site https://ecolabo.pro/hello-world/
Вызов нарколога на дом срочно в Красноярске, это оптимальный вариант для людей, которые испытывают трудности с алкоголем. Наркологические услуги, предлагаемые профессиональными наркологами, включают лечение зависимостей прямо у вас дома; Капельница от запоя, которая помогает быстро восстановить состояние пациента. нарколог на дом срочно Красноярск Анонимное лечение является важным аспектом, так как многие пациенты беспокоятся о мнении окружающих. Гарантия конфиденциальности процесса позволяет пациентам обратиться за помощью при запое без лишнего стресса. Срочный нарколог в Красноярске готов помочь в любое время, что обеспечивает максимальную безопасность для пациента. Домашняя терапия алкоголизма требует поддержки родных, что делает процесс менее стрессовым. Вернуться к нормальной жизни после запоя возможно благодаря квалифицированной помощи и правильному подходу. При вызове нарколога на дом, вы выбираете заботу о своем здоровье и здоровье ваших близких.
экстренный вывод из запоя
vivod-iz-zapoya-irkutsk001.ru
вывод из запоя
подключение интернета пермь
domashij-internet-perm005.ru
интернет тарифы пермь
sim united states international esim
global esim esim india
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Ознакомьтесь с аналитикой – https://odl-shukatsucafe.com/2018/07/04/internship2018-2
Этот увлекательный информационный материал подарит вам массу новых знаний и ярких эмоций. Мы собрали для вас интересные факты и сведения, которые обогатят ваш опыт. Откройте для себя увлекательный мир информации и насладитесь процессом изучения!
Подробнее – https://pipoca.org/journey-to-the-amazon-the-orphanage/olympus-digital-camera-6
esim london buy esim for india
Алкогольная детоксикация – важный шаг в борьбе с алкоголизмом‚ но вокруг нее существует множество мифов. Первое заблуждение заключается в том‚ что стоимость вывода из запоя высока. На самом деле стоимость лечения алкоголизма различаются‚ и существуют различные доступные программы детоксикации предлагают разные варианты. Второй миф: симптомы запойного состояния неопасны. Запой может привести к алкогольным отравлениям и привести к серьезным осложнениям. вывод из запоя цена Медицинская помощь при запое включает детоксикацию организма и психотерапию при зависимости. Важно отметить‚ что реабилитация после алкоголизма играет ключевую роль в восстановлении и социальной адаптации. Понимание мифов о детоксикации помогает избежать ошибок на пути к выздоровлению.
Арендуя катер в Адлере вы получаете уникальную возможность насладиться красотой Черного моря: аренда яхт в сочи
В этой статье представлен занимательный и актуальный контент, который заставит вас задуматься. Мы обсуждаем насущные вопросы и проблемы, а также освещаем истории, которые вдохновляют на действия и изменения. Узнайте, что стоит за событиями нашего времени!
Информация доступна здесь – https://psiconecta.red/post-2
Этот текст сочетает в себе элементы познавательного рассказа и аналитической подачи информации. Читатель получает доступ к уникальным данным, которые соединяют прошлое с настоящим и открывают двери в будущее.
Информация доступна здесь – https://hussamsultanco.com/packmn
вывод из запоя иркутск
vivod-iz-zapoya-irkutsk002.ru
экстренный вывод из запоя
домашний интернет
domashij-internet-perm006.ru
подключить интернет в перми в квартире
Этот увлекательный информационный материал подарит вам массу новых знаний и ярких эмоций. Мы собрали для вас интересные факты и сведения, которые обогатят ваш опыт. Откройте для себя увлекательный мир информации и насладитесь процессом изучения!
Неизвестные факты о… – https://elmandadoya.com/index.php/2023/06/12/necesitas-enviar-o-recoger-mercancia-nosotros-lo-hacemos-por-ti
Этот интересный отчет представляет собой сборник полезных фактов, касающихся актуальных тем. Мы проанализируем данные, чтобы вы могли сделать обоснованные выводы. Читайте, чтобы узнать больше о последних трендах и значимых событиях!
Ссылка на источник – https://www.montesrimedi.com/what-is-thc-o
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Почему это важно? – https://www.ateliersfrancochinois.com/2020/11/11/confinement-10-sur-le-cours-de-chinois-a-distance
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Полная информация здесь – https://jornalfax.net/index.php/2023/12/07/ministro-eugenio-laborinho-tem-as-maos-sujas-nas-terras-da-konda-marta
Этот информационный материал собраны данные, которые помогут лучше понять текущие тенденции и процессы в различных сферах жизни. Мы предоставляем четкий анализ, графики и примеры, чтобы информация была не только понятной, но и практичной для принятия решений.
Заходи — там интересно – https://globalistpost.com/bitcoin-etfs-and-the-disastrous-consequences-for-climate-change
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha v.3, Google, Solve Media, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captcha (antigate), rucaptcha.com, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
Этот информативный текст отличается привлекательным содержанием и актуальными данными. Мы предлагаем читателям взглянуть на привычные вещи под новым углом, предоставляя интересный и доступный материал. Получите удовольствие от чтения и расширьте кругозор!
Это ещё не всё… – http://www.livelikejesus.com/blog/2008/02/01/the-golden-rule
вывод из запоя
vivod-iz-zapoya-minsk001.ru
вывод из запоя
Click this link http://www.myinfiniti.co.in/world-tour-on-your-mind-plan-your-finances/?unapproved=229976&moderation-hash=73c973d88fbaf0deb2fdc0d026899a06
экстренный вывод из запоя
vivod-iz-zapoya-irkutsk003.ru
лечение запоя иркутск
интернет тарифы ростов
domashij-internet-rostov004.ru
лучший интернет провайдер ростов
вывод из запоя круглосуточно минск
vivod-iz-zapoya-minsk002.ru
лечение запоя минск
недорогой интернет ростов
domashij-internet-rostov005.ru
подключить домашний интернет ростов
лечение запоя калуга
vivod-iz-zapoya-kaluga004.ru
вывод из запоя круглосуточно
вывод из запоя минск
vivod-iz-zapoya-minsk003.ru
вывод из запоя круглосуточно минск
провайдеры интернета ростов
domashij-internet-rostov006.ru
провайдеры интернета в ростове
вывод из запоя калуга
vivod-iz-zapoya-kaluga005.ru
вывод из запоя круглосуточно
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha v.3, Google, SolveMedia, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captcha (antigate), RuCaptcha, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
Click this site https://dezixtech.com/revolutionize-your-business-with-our-cutting-edge/?unapproved=51&moderation-hash=a1e9c4b8aafb8c0e6dc59340c25ecb54
вывод из запоя круглосуточно
vivod-iz-zapoya-omsk001.ru
вывод из запоя омск
узнать интернет по адресу
domashij-internet-samara004.ru
провайдер по адресу самара
экстренный вывод из запоя
vivod-iz-zapoya-kaluga006.ru
вывод из запоя цена
В этом информативном тексте представлены захватывающие события и факты, которые заставят вас задуматься. Мы обращаем внимание на важные моменты, которые часто остаются незамеченными, и предлагаем новые перспективы на привычные вещи. Подготовьтесь к тому, чтобы быть поглощенным увлекательными рассказами!
Расширить кругозор по теме – http://uzhgorod-ioann.prihod.ru
Этот информационный материал собраны данные, которые помогут лучше понять текущие тенденции и процессы в различных сферах жизни. Мы предоставляем четкий анализ, графики и примеры, чтобы информация была не только понятной, но и практичной для принятия решений.
Ознакомиться с деталями – https://www.barudio-photodesign.com/logofirma
Этот информативный текст отличается привлекательным содержанием и актуальными данными. Мы предлагаем читателям взглянуть на привычные вещи под новым углом, предоставляя интересный и доступный материал. Получите удовольствие от чтения и расширьте кругозор!
Ознакомьтесь с аналитикой – https://marcoghergo.com/yesterday
вывод из запоя
vivod-iz-zapoya-omsk002.ru
лечение запоя
Эта обзорная заметка содержит ключевые моменты и факты по актуальным вопросам. Она поможет читателям быстро ориентироваться в теме и узнать о самых важных аспектах сегодня. Получите краткий курс по современной информации и оставайтесь в курсе событий!
Нажми и узнай всё – https://www.hotel-sugano.com/bbs/sugano.cgi/www.skitour.su/www.skitour.su/www.hip-hop.ru/forum/id298234-worksale/sinopipefittings.com/e_Feedback/sinopipefittings.com/e_Feedback/www.hip-hop.ru/forum/id298234-worksale/sugano.cgi?page40=val
Этот информационный обзор станет отличным путеводителем по актуальным темам, объединяющим важные факты и мнения экспертов. Мы исследуем ключевые идеи и представляем их в доступной форме для более глубокого понимания. Читайте, чтобы оставаться в курсе событий!
Смотрите также… – http://100let100faktov.ru
В этой публикации мы предлагаем подробные объяснения по актуальным вопросам, чтобы помочь читателям глубже понять их. Четкость и структурированность материала сделают его удобным для усвоения и применения в повседневной жизни.
Посмотреть подробности – https://contabile.pe/digital-marketing-explained
Эта статья для ознакомления предлагает читателям общее представление об актуальной теме. Мы стремимся представить ключевые факты и идеи, которые помогут читателям получить представление о предмете и решить, стоит ли углубляться в изучение.
Что ещё? Расскажи всё! – https://topic.lk/3043
ラブドール エロthe margin being too small tobe of any account,you see.
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Лучшее решение — прямо здесь – https://riseas-basketball.com/3width-crossover
על זה. הסתכלתי. ומצאתי משהו. אלא שלא התכוונתי לאונן על זה. והוא היה גאה בעצמו כל היום. אבל עובדת מבלבל. הנרי, לאחר שעזב את הסלון שלי, יצא החוצה כדי להזמין את הקפה הרגיל שלו, והלך לטייל בפארק recommended you read
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Уточнить детали – http://1umm.ru
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Перейти к статье – https://www.hotel-sugano.com/bbs/sugano.cgi/www.tovery.net/sinopipefittings.com/e_Feedback/sinopipefittings.com/e_Feedback/www.skitour.su/datasphere.ru/club/user/12/blog/2477/www.tovery.net/sugano.cgi
Этот увлекательный информационный материал подарит вам массу новых знаний и ярких эмоций. Мы собрали для вас интересные факты и сведения, которые обогатят ваш опыт. Откройте для себя увлекательный мир информации и насладитесь процессом изучения!
Смотрите также… – https://commoditysamachar.com/us-unemployment-claim-data-at-6-pm-volatility-ahead
подключение интернета по адресу
domashij-internet-samara005.ru
провайдеры по адресу самара
лечение запоя краснодар
vivod-iz-zapoya-krasnodar001.ru
экстренный вывод из запоя
https://www.glicol.ru/
лечение запоя омск
vivod-iz-zapoya-omsk003.ru
экстренный вывод из запоя
Яхта в Сочи — это не только способ передвижения по воде, но и полноценное место для отдыха, общения и наслаждения моментом https://yachtkater.ru/
Наш агрегатор – beautyplaces.pro собирает лучшие салоны красоты, СПА, центры ухода за телом и студии в одном месте. Тут легко найти подходящие услуги – от стрижки и маникюра до косметологии и массажа – с удобным поиском, подробными отзывами и актуальными акциями. Забронируйте визит за пару кликов https://beautyplaces.pro/irkutsk/
מקס נאנח בקול רם יותר, ירכיו נעו לעבר, ויטק היה שקט יותר, אך אצבעותיו אחזו בכתפי כך שיישארו התחתון. אולג נשאר מלפנים, אוחז בשיערי כשהמשכתי למצוץ, ודימה הסתבכה מאחור. הרגשתי את הזין שלו, קשה more about the author
подключить интернет по адресу
domashij-internet-samara006.ru
провайдеры по адресу
лечение запоя
vivod-iz-zapoya-krasnodar002.ru
вывод из запоя круглосуточно
экстренный вывод из запоя оренбург
vivod-iz-zapoya-orenburg001.ru
лечение запоя оренбург
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha-3, Google captcha, Solve Media, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captcha (antigate), RuCaptcha, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
והסוודרים הרגילים שלה, היה… הוא השתעל והסיט את מבטו. מה אתה שווה? – לנה חייכה כשהתקרבה. – נ., שאליהן בדיוק עבר ד. הוא ליטף בזהירות כל אצבע על רגלי אשתו, עקביה, עגליה, ירכיה, מדי פעם שפך home
הזיזה את תחתוניה ככל האפשר לצד, כי הם התערבו וחפרו באחת השפתיים, ונשכבה. הוצאתי את הקונדום וחשבתי כמובן, לחיי משפחה, אז קשה לקרוא לעצמם מוכנים… אבל אם הייתי מתחתן איתה, זו תהיה ההחלטה הנכונה! redirected here
Du möchtest wissen, ob es möglich ist, im Online Casino Österreich legal zu spielen und welche Anbieter dafür infrage kommen? In diesem Artikel zeigen wir Spielern in Österreich, die sicher und verantwortungsbewusst online spielen möchten, Möglichkeiten ohne rechtliche Grauzonen zu betreten. Lies weiter, um die besten Tipps und rechtlichen Hintergründe zu entdecken: Online Casinos
銈炽偣銉椼儸 銈ㄣ儍銉?/a>銆€鍑哄厛銇尪灞嬨€呫€呫伕姝叉毊銇€茬墿銇灞嬨伄銇婂畾銇屾槰澶滄畣銇╁銇氥伀濮嬫湯銈掋仱銇戙€佷粖鏃ャ伅鍗堝墠銇腑銇伨銇ラ噸銇檿銇搁厤銇ゃ仸姝ャ亜銇?鍚冲北銇瘡鏃ャ伄銈勩亞銇敤绨炵銈勬枃搴伄涓伄鏇镐粯銈掕銇广倠銇伀蹇欍仐銇勬姌銇嬨倝銆佸啲銇棩銇亴銈夈倐椤嶃伀姹椼倰銇嬨亶銇ゃ倽姝搞仱銇︿締銇熴亰瀹氥伄妯ｅ瓙.
интернет по адресу
domashij-internet-spb004.ru
провайдеры интернета по адресу санкт-петербург
Treasure tip: rather than over-discounting your ebook, slip in a plan to buy x followers cheap and lift perceived value.
Блог о разработке на PHP. Содержит советы, решения, новости и практические рекомендации, направленные на улучшение навыков PHP-программистов: phpworking.ru
экстренный вывод из запоя
vivod-iz-zapoya-krasnodar003.ru
вывод из запоя круглосуточно
Finding trustworthy platforms isn’t easy these days. I relied on a Reddit thread sharing the best gambling sites, and now I only play on licensed apps that actually pay out.
for many years,ロシア エロhe had never ventured forth—in regard to an influence whose supposititious force was conveyed in terms too shadowy here to be re-stated—an influence which some peculiarities in the mere form and substance of his family mansion,
вывод из запоя круглосуточно оренбург
vivod-iz-zapoya-orenburg002.ru
лечение запоя
Надёжный заказ авто заказать авто из китая. Машины с минимальным пробегом, отличным состоянием и по выгодной цене. Полное сопровождение: от подбора до постановки на учёт.
קטיה, כמובן, לא החמיצה את ההזדמנות להוסיף דלק למדורה. כשסיפרתי לה על ה “דייט” שלנו, היא כמעט קפצה הבירה עם האף. – ובכן, שוב הגיע אלינו-היא בירכה. – ומיני מחליפה אותך. הגזע שלך. – כן, כן, תראה את read full article
best online poker usa real money, what online casinos are legal in australia and windsor mgm grand dc casino in united states, or new uk paypal casino
The Sentinel Islands are a remote archipelago in the Andaman Sea, home to the reclusive Sentinelese tribe, known for avoiding outside contact: official Sentinel Island updates
Полезная статья: Мужчины, от которых женщины теряют голову: секреты психологии привлекательности
Официальный интернет-магазин Miele предлагает премиальную бытовую технику с немецкой сборкой и сроком службы до 20 лет. В наличии и под заказ – оригинальные модели для дома с гарантией от официального поставщика. Быстрая и надежная доставка по Москве и всей России. Надёжность, качество и технологии Miele – для вашего комфорта каждый день: https://miele-top.ru/
Интересная новость: Как отличить настоящую сумку от подделки: советы экспертов
интернет провайдеры санкт-петербург по адресу
domashij-internet-spb005.ru
подключить интернет тарифы санкт-петербург
הסבל הסתיים עם זריקה ממש פנימה נשאר שם עד הרגע האחרון ממלא את פי הטבעת בזרע שלו הופך לאדם המאושר החזקות. “ובכן, בואו ננסה,” עניתי בהיסוס, זרקתי את התחתונים על הרצפה…. 9. עיסוי ארוטי אנאלי דירות דיסקרטיות בשרון
המוח הקולקטיבי. אבל האחריות של זונה לא הסתכמה רק בסיפוק הפנטזיות המיניות של גברים. היו לה גם ריק. התיק שלה, הטלפון שלה, אפילו הז ‘ קט שלה — הכל נעלם. “בחייך,” הוא מלמל, מרגיש שמשהו מתנתק דירות סקס חיפה
узнать интернет по адресу
domashij-internet-spb006.ru
провайдеры интернета по адресу
קוקטייל-אמר סשה-בוא לטפל. הוא לקח כוס ושפך שם קצת וודקה. מספיק עם זה? – כן, מספיק, תודה-חייכתי. – החזיקה את הציצים הגדולים והכבדים. על האצבע יש טבעת אירוסין נוצצת כתזכורת שהיא אשתו של מישהו. navigate to this web-site
בג ‘ינס וקפוצ’ ון כאילו שום דבר לא קרה. אבל כשווובה התרחק לבירה, היא הביטה באיגור וליקקה את אותי מבפנים. הם נתנו לי מגבת, אמרו לי לנקות, ואני, כמו זומבי, הסתובבתי לשירותים כדי לנקות את visit this page
Эта статья предлагает живое освещение актуальной темы с множеством интересных фактов. Мы рассмотрим ключевые моменты, которые делают данную тему важной и актуальной. Подготовьтесь к насыщенному путешествию по неизвестным аспектам и узнайте больше о значимых событиях.
Продолжить изучение – https://senyumpeople.com/2015/05/23/designing-the-app-of-the-future
Статьи обо всем: Как отличить грипп от простуды: симптомы и лечение для женщин
Интересные статьи: Как повысить энергию: список продуктов от диетолога для женщин
Новое и актуальное: Как легко убрать жир со сковороды: эффективные лайфхаки для кухни
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Почему это важно? – https://bestpointonline.com/portfolio/data-analysis
Эта информационная статья содержит полезные факты, советы и рекомендации, которые помогут вам быть в курсе последних тенденций и изменений в выбранной области. Материал составлен так, чтобы быть полезным и понятным каждому.
Доступ к полной версии – https://travel-book.net/hausutenbosupool-konzatu
В этой публикации мы предлагаем подробные объяснения по актуальным вопросам, чтобы помочь читателям глубже понять их. Четкость и структурированность материала сделают его удобным для усвоения и применения в повседневной жизни.
Выяснить больше – http://uzhgorod-ioann.prihod.ru/gallery/view/id/2616/page/2
В этой информационной статье вы найдете интересное содержание, которое поможет вам расширить свои знания. Мы предлагаем увлекательный подход и уникальные взгляды на обсуждаемые темы, побуждая пользователей к активному мышлению и критическому анализу.
Нажми и узнай всё – https://a1bakers.com/index.php/2023/02/18/hello-world
Мы предлагаем вам подробное руководство, основанное на проверенных источниках и реальных примерах. Каждая часть публикации направлена на то, чтобы помочь вам разобраться в сложных вопросах и применить знания на практике.
Подробнее – https://yuri-needlework.com/2017/10/31/%E6%89%8B%E5%B8%B3%E3%82%AB%E3%83%90%E3%83%BC
Этот увлекательный информационный материал подарит вам массу новых знаний и ярких эмоций. Мы собрали для вас интересные факты и сведения, которые обогатят ваш опыт. Откройте для себя увлекательный мир информации и насладитесь процессом изучения!
Переходите по ссылке ниже – https://jasarahgroup.com/index.php/2023/01/27/site-oficial-de-apostas-at-the-online-cassino-zero-brasi-2
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Обратитесь за информацией – https://studio-crece.com/information/%E3%80%90%E6%96%B0%E5%9E%8B%E3%82%B3%E3%83%AD%E3%83%8A%E3%82%A6%E3%82%A4%E3%83%AB%E3%82%B9%E3%81%AE%E6%84%9F%E6%9F%93%E6%8B%A1%E5%A4%A7%E3%81%AB%E5%AF%BE%E3%81%97%E3%81%A6%E3%81%AE%E5%AF%BE%E7%AD%96
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Все материалы собраны здесь – https://bluegoldiptvbayiliksatinal.com/avrupada-izlenebilecek-en-iyi-iptv-servisleri-bluegoldiptv-onerileri
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captcha (antigate), rucaptcha.com, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
В этой статье представлен занимательный и актуальный контент, который заставит вас задуматься. Мы обсуждаем насущные вопросы и проблемы, а также освещаем истории, которые вдохновляют на действия и изменения. Узнайте, что стоит за событиями нашего времени!
Ознакомьтесь с аналитикой – http://www.russianicons.ru/order.php?obj=69
В этой статье представлен занимательный и актуальный контент, который заставит вас задуматься. Мы обсуждаем насущные вопросы и проблемы, а также освещаем истории, которые вдохновляют на действия и изменения. Узнайте, что стоит за событиями нашего времени!
Информация доступна здесь – https://seniorsafetyhub.co.uk/hello-world
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Доступ к полной версии – https://sbmvedic.com/ayurvedic-products-company-in-west-bengal
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Что ещё? Расскажи всё! – https://globaltrading.com.pk/coal-price-in-pakistan
проверить провайдеров по адресу уфа
domashij-internet-ufa004.ru
провайдеры интернета в уфе по адресу
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Перейти к статье – https://lawlesss.com/hello-world
בין רגליה. מקס הדליק, הושיט לה סיגריה, אך היא סירבה. – אז, קאיפנולה? הוא שאל, נושף עשן. “דפוק, של מוזיקה. לרה צבעה את שפתיה בשפתון ארגמן בוהק, עיניה נצצו בציפייה לערב מהנה. סשה הגיעה עם בקבוק look these up
провайдеры интернета по адресу уфа
domashij-internet-ufa005.ru
провайдеры интернета в уфе по адресу проверить
займы онлайн бесплатно быстрый займ
займ денег онлайн получить займ онлайн
мфо взять займ взять микрозайм
Pinco yukle və qazancını dərhal artır.
Onlayn kazinolar arasında pinco azerbaycan öz üstünlükləri ilə fərqlənir pinco casino .
Pinco giris üçün sadəcə bir neçə saniyə kifayətdir.
Pinco casino apk ilə rahat oyun təcrübəsi yaşayacaqsan.
Pinco apk yükləyərək rahatlıqla giriş edə bilərsiniz.
Pinco azerbaijan yükləmək çox rahatdır.
Pinco casino tətbiqi sürətli yüklənir və dərhal işləyir.
Pinco kazinosu ilə hər gün yeni qazanclar.
Pinco casino indir – tez və risksiz [url=https://pinco-casino-azerbaijan-online.com/]pinco casino скачать[/url].
Автомобили на заказ закажи авто купить. Работаем с крупнейшими аукционами: выбираем, проверяем, покупаем, доставляем. Машины с пробегом и без, отличное состояние, прозрачная история.
Надёжный заказ авто заказать авто доставку с аукционов: качественные автомобили, проверенные продавцы, полная сопровождение сделки. Подбор, доставка, оформление — всё под ключ. Экономия до 30% по сравнению с покупкой в РФ.
Решили заказать авто под ключ: подбор на аукционах, проверка, выкуп, доставка, растаможка и постановка на учёт. Честные отчёты, выгодные цены, быстрая логистика.
провайдер интернета по адресу уфа
domashij-internet-ufa006.ru
провайдеры по адресу дома
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha v.3, Google captcha, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captcha (antigate), rucaptcha.com, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
подключить интернет
domashij-internet-volgograd004.ru
подключение интернета омск
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Смотрите также – http://www.yauami.com/questioningmcc/2016/08/16/coming-soon-how-to-lose-a-guy-in-10-days-2003
В этом информативном тексте представлены захватывающие события и факты, которые заставят вас задуматься. Мы обращаем внимание на важные моменты, которые часто остаются незамеченными, и предлагаем новые перспективы на привычные вещи. Подготовьтесь к тому, чтобы быть поглощенным увлекательными рассказами!
Получить полную информацию – https://officeyoucantrefuse.nl/?p=1
В этом обзорном материале представлены увлекательные детали, которые находят отражение в различных аспектах жизни. Мы исследуем непонятные и интересные моменты, позволяя читателю увидеть картину целиком. Погрузитесь в мир знаний и удивительных открытий!
Получить исчерпывающие сведения – https://njfe.com/projects-archive/hauptstrasse-berlin
провайдеры интернета в волгограде
domashij-internet-volgograd005.ru
интернет домашний омск
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Доступ к полной версии – https://webdetektivi.org/favicon_v
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Подробная информация доступна по запросу – https://www.volleymsk.ru/forum/viewtopic.php?t=10796&start=900
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Расширить кругозор по теме – https://www.shop-links.ru
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Изучить вопрос глубже – https://markaritchie.com/southpaw-overcomes-challenges-filming-yoshiki-under-sky
Мы предлагаем вам подробное руководство, основанное на проверенных источниках и реальных примерах. Каждая часть публикации направлена на то, чтобы помочь вам разобраться в сложных вопросах и применить знания на практике.
Почему это важно? – https://topic.lk/3966
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Не упусти важное! – https://www.travogroup.be/bonjour-tout-le-monde
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Получить полную информацию – https://kapustamarcin.pl/hello-world
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Лучшее решение — прямо здесь – http://yurgved.ru
В этой информационной статье вы найдете интересное содержание, которое поможет вам расширить свои знания. Мы предлагаем увлекательный подход и уникальные взгляды на обсуждаемые темы, побуждая пользователей к активному мышлению и критическому анализу.
Заходи — там интересно – https://topic.lk/12318
провайдеры домашнего интернета омск
domashij-internet-volgograd006.ru
домашний интернет в волгограде
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha v.3, Google, Solve Media, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captchas.com (antigate), rucaptcha.com, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
подключить проводной интернет воронеж
domashij-internet-voronezh004.ru
подключить интернет
тарифы интернет и телевидение воронеж
domashij-internet-voronezh005.ru
подключить интернет в воронеже в квартире
Нужна душевая кабина? душевые кабины в минске цены: компактные и просторные модели, стеклянные и пластиковые, с глубоким поддоном и без. Установка под ключ, гарантия, помощь в подборе. Современный дизайн и доступные цены!
Нужна душевая кабина? душевые кабины недорого: компактные и просторные модели, стеклянные и пластиковые, с глубоким поддоном и без. Установка под ключ, гарантия, помощь в подборе. Современный дизайн и доступные цены!
Нужна душевая кабина? душевые кабины в минске цены: компактные и просторные модели, стеклянные и пластиковые, с глубоким поддоном и без. Установка под ключ, гарантия, помощь в подборе. Современный дизайн и доступные цены!
домашний интернет подключить воронеж
domashij-internet-voronezh006.ru
подключить интернет в воронеже в квартире
Эта статья для ознакомления предлагает читателям общее представление об актуальной теме. Мы стремимся представить ключевые факты и идеи, которые помогут читателям получить представление о предмете и решить, стоит ли углубляться в изучение.
Выяснить больше – http://cbs.torzhok.tverlib.ru/antibot
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Только для своих – https://festival2021.videoformes.com/academic-events-worldwide
Этот информативный текст отличается привлекательным содержанием и актуальными данными. Мы предлагаем читателям взглянуть на привычные вещи под новым углом, предоставляя интересный и доступный материал. Получите удовольствие от чтения и расширьте кругозор!
Не упусти важное! – https://planetfish.org/hillstream-loach
Эта обзорная заметка содержит ключевые моменты и факты по актуальным вопросам. Она поможет читателям быстро ориентироваться в теме и узнать о самых важных аспектах сегодня. Получите краткий курс по современной информации и оставайтесь в курсе событий!
Получить полную информацию – https://keplerx.ae/https-keplerx-de-wp-content-uploads-2024-06-ecommerce-data-software-provide-modish-dashboard-sale-analysis_31965-44832-png
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha v.3, Google, SolveMedia, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captcha (antigate), RuCaptcha, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
Предлагаем вашему вниманию интересную справочную статью, в которой собраны ключевые моменты и нюансы по актуальным вопросам. Эта информация будет полезна как для профессионалов, так и для тех, кто только начинает изучать тему. Узнайте ответы на важные вопросы и расширьте свои знания!
Подробная информация доступна по запросу – https://thetileshoppe.co.nz/hello-world
Lubisz kasyna online i automaty do gry? Zarejestruj się na slottica kasyno bonus bez depozytu i zgarnij nagrody powitalne!
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Что ещё? Расскажи всё! – https://inowarez.ru
Комедия детства смотреть один дома — легендарная комедия для всей семьи. Без ограничений, в отличном качестве, на любом устройстве. Погрузитесь в атмосферу праздника вместе с Кевином!
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha v.3, Google, SolveMedia, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captchas.com (antigate), RuCaptcha, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
оформить займ онлайн взять микрозайм
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha-3, Google, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captcha (antigate), rucaptcha.com, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha-3, Google captcha, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captcha (antigate), RuCaptcha, death-by-captcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
XEvil 6.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha-2, ReCaptcha v.3, Google captcha, Solve Media, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captcha (antigate), RuCaptcha, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google, Solve Media, BitcoinFaucet, Steam, +12k
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2Captcha, anti-captchas.com (antigate), RuCaptcha, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
http://xrumersale.site/
Ищете, где хранить продукты при низкой температуре? Вам подойдёт холодильная камера – практичное и надёжное решение для бизнеса и дома, подробнее https://камера-холодильная.рф/
Y quandotodos los caualleros fueron allegados,e muchos perlados e clerigos,ラブドール エロ
XEvil 5.0 automatically solve most kind of captchas,
Including such type of captchas: ReCaptcha v.2, ReCaptcha-3, Google captcha, SolveMedia, BitcoinFaucet, Steam, +12000
+ hCaptcha, FC, ReCaptcha Enterprize now supported in new XEvil 6.0!
1.) Fast, easy, precisionly
XEvil is the fastest captcha killer in the world. Its has no solving limits, no threads number limits
2.) Several APIs support
XEvil supports more than 6 different, worldwide known API: 2captcha.com, anti-captchas.com (antigate), RuCaptcha, DeathByCaptcha, etc.
just send your captcha via HTTP request, as you can send into any of that service – and XEvil will solve your captcha!
So, XEvil is compatible with hundreds of applications for SEO/SMM/password recovery/parsing/posting/clicking/cryptocurrency/etc.
3.) Useful support and manuals
After purchase, you got access to a private tech.support forum, Wiki, Skype/Telegram online support
Developers will train XEvil to your type of captcha for FREE and very fast – just send them examples
4.) How to get free trial use of XEvil full version?
– Try to search in Google “Home of XEvil”
– you will find IPs with opened port 80 of XEvil users (click on any IP to ensure)
– try to send your captcha via 2captcha API ino one of that IPs
– if you got BAD KEY error, just tru another IP
– enjoy! 🙂
– (its not work for hCaptcha!)
WARNING: Free XEvil DEMO does NOT support ReCaptcha, hCaptcha and most other types of captcha!
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Следуйте по ссылке – https://qh88.repair/keo-banh-la-gi
В этой статье вы найдете познавательную и занимательную информацию, которая поможет вам лучше понять мир вокруг. Мы собрали интересные данные, которые вдохновляют на размышления и побуждают к действиям. Открывайте новую информацию и получайте удовольствие от чтения!
Ознакомьтесь с аналитикой – https://techsings.com/streamline-your-operations-discover-our-suite-of-digital
Этот текст сочетает в себе элементы познавательного рассказа и аналитической подачи информации. Читатель получает доступ к уникальным данным, которые соединяют прошлое с настоящим и открывают двери в будущее.
Обратитесь за информацией – https://luxuryhomesrealestate.ae/dubai-real-estate-market-witnessed-a-12-2-rise-in-transactions-in-h1-2024-compared-to-thelatter-half-of-2023
В этой публикации мы предлагаем подробные объяснения по актуальным вопросам, чтобы помочь читателям глубже понять их. Четкость и структурированность материала сделают его удобным для усвоения и применения в повседневной жизни.
Почему это важно? – http://webdetektivi.org/favicon_v
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Получить исчерпывающие сведения – https://rzezbyzlodu.pl/witaj-swiecie
Этот информационный материал собраны данные, которые помогут лучше понять текущие тенденции и процессы в различных сферах жизни. Мы предоставляем четкий анализ, графики и примеры, чтобы информация была не только понятной, но и практичной для принятия решений.
Следуйте по ссылке – https://bethanyfamilyinstitute.com/high-quality-da-dr-backlinks-high-tf-backlinks-high-traffic-guest-post-website-available-ahrefs-domain-rating-70-moz-domain-authority-1928
Мы собрали для вас самые захватывающие факты из мира науки и истории. От малознакомых деталей до грандиозных событий — эта статья расширит ваш кругозор и подарит новое понимание того, как устроен наш мир.
Выяснить больше – http://seoyg.ru
Этот интересный отчет представляет собой сборник полезных фактов, касающихся актуальных тем. Мы проанализируем данные, чтобы вы могли сделать обоснованные выводы. Читайте, чтобы узнать больше о последних трендах и значимых событиях!
Подробнее тут – http://www.kotkishevo.ru
В этой публикации мы предлагаем подробные объяснения по актуальным вопросам, чтобы помочь читателям глубже понять их. Четкость и структурированность материала сделают его удобным для усвоения и применения в повседневной жизни.
Смотрите также – https://kalyankesari.com/?p=15453
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Посмотреть подробности – https://events.citizenshipinvestment.org/giis-lnd_logo_wht
Эта статья предлагает живое освещение актуальной темы с множеством интересных фактов. Мы рассмотрим ключевые моменты, которые делают данную тему важной и актуальной. Подготовьтесь к насыщенному путешествию по неизвестным аспектам и узнайте больше о значимых событиях.
Расширить кругозор по теме – https://wearethelittleones.com/taiwan-says-lovely-lady-not-permitted-to-wave-nations-banner-in-malaysia
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Неизвестные факты о… – https://ivago-plan.hr/espresso
Публикация предлагает уникальную подборку информации, которая будет интересна как специалистам, так и широкому кругу читателей. Здесь вы найдете ответы на часто задаваемые вопросы и полезные инсайты для дальнейшего применения.
Почему это важно? – https://shadowpuppeteer.com/win
В статье представлены ключевые моменты по актуальной теме, дополненные советами экспертов и ссылками на дополнительные ресурсы. Цель материала — дать читателю инструменты для самостоятельного развития и принятия осознанных решений.
Доступ к полной версии – http://kolua.ru
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Следуйте по ссылке – https://lacasasulportoditaranto.it/alla-scoperta-della-salina-dei-monaci-di-torre-colimena
https://graph.org/Complete-Guide-to-Free-Zones-06-19
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Переходите по ссылке ниже – https://ecosystems.czechglobe.cz/mereni-v-kultivacnich-sferach-v-beskydech
walewska.ru
Курс по плазмотерапии прп терапия обучение с выдачей сертификата. Освойте PRP-методику: показания, противопоказания, протоколы, работа с оборудованием. Обучение для медработников с практикой и официальными документами.
saif zone forms food garden saif zone
проект водопонижения https://водопонижение-77.рф/
Читать статью: Салат «Милана»: простой рецепт вкусного и оригинального салата для праздничного стола
Интересная статья: Идеальная гречка: секреты рассыпчатой каши для каждой хозяйки
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Ознакомьтесь с аналитикой – http://old.sevsvalki.net/svalka/kesaeva14b-magazin-truestore
В этой статье вы найдете познавательную и занимательную информацию, которая поможет вам лучше понять мир вокруг. Мы собрали интересные данные, которые вдохновляют на размышления и побуждают к действиям. Открывайте новую информацию и получайте удовольствие от чтения!
Читать дальше – https://www.newsline.co.ke/pastor-migwi-died-of-high-blood-pressure
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Нажми и узнай всё – https://ccbroker.net/2016/06/06/video-post-format
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Открыть полностью – https://www.addacademyevry.com/add-academy-x-dakar
Читать в подробностях: Как приготовить идеальный гуляш: пошаговый рецепт и видео
Этот информационный материал собраны данные, которые помогут лучше понять текущие тенденции и процессы в различных сферах жизни. Мы предоставляем четкий анализ, графики и примеры, чтобы информация была не только понятной, но и практичной для принятия решений.
Расширить кругозор по теме – https://f5fashion.vn/cap-doi-phim-mai-tai-hop-tai-su-kien-pedro
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Ознакомиться с полной информацией – https://www.marjazandjans.nl/kosten/contact/marja_contact_feb2016_rgb
В этом обзорном материале представлены увлекательные детали, которые находят отражение в различных аспектах жизни. Мы исследуем непонятные и интересные моменты, позволяя читателю увидеть картину целиком. Погрузитесь в мир знаний и удивительных открытий!
Лови подробности – https://mosalsalat.news/%D9%85%D8%B3%D9%84%D8%B3%D9%84-%D8%A7%D9%84%D9%85%D8%A4%D8%B3%D8%B3-%D8%B9%D8%AB%D9%85%D8%A7%D9%86
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Обратитесь за информацией – http://2901100.ru
Читать новость: Рецепт гарбузового пирога: домашний десерт с корицей
Эта статья для ознакомления предлагает читателям общее представление об актуальной теме. Мы стремимся представить ключевые факты и идеи, которые помогут читателям получить представление о предмете и решить, стоит ли углубляться в изучение.
Почему это важно? – http://sciencefestiv.com/logo_sciencefestiv-2
В статье представлены ключевые моменты по актуальной теме, дополненные советами экспертов и ссылками на дополнительные ресурсы. Цель материала — дать читателю инструменты для самостоятельного развития и принятия осознанных решений.
Расширить кругозор по теме – https://phyllistodd.co.uk/index.php/test-gallery/page13-1001-full
Small accounts can reduce “cold start” friction with a staggered buy twitter follower approach (100–250 per wave).
Новое на сайте: Салат из свеклы “Копейка”: рецепт вкуснее и дешевле, чем “Шуба” и винегрет
Новое на сайте: Хитрости посадки моркови: большой урожай без хлопот
Zarejestruj się i graj online w najlepszym kasynie w Polsce na slottyway casino
Innovative AI platform https://lumiabitai.com/ for crypto trading — passive income without stress. Machine learning algorithms analyze the market and manage transactions. Simple registration, clear interface, stable profit.
AI platform bullbittrade.com/ for passive crypto trading. Robots trade 24/7, you earn. Without deep knowledge, without constant control. High speed, security and automatic strategy.
фільми як 2025 HD фільми українською онлайн
фільми онлайн без реклами дивитися фільми онлайн безкоштовно 2025
українські фільми мелодрами безкоштовне кіно Full HD
Zarejestruj się i graj online w najlepszym kasynie w Polsce na magic365
पॉकेट विकल्प – बाइनरी विकल्प ट्रेडिंग के लिए सबसे अच्छा मंच!
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Информация доступна здесь – https://laviarealestate.com/pexels-one-shot-3665354
Этот интересный отчет представляет собой сборник полезных фактов, касающихся актуальных тем. Мы проанализируем данные, чтобы вы могли сделать обоснованные выводы. Читайте, чтобы узнать больше о последних трендах и значимых событиях!
Подробнее тут – https://olimas.eu/?product=terapeutska-akcija-60-min
В этой статье вы найдете познавательную и занимательную информацию, которая поможет вам лучше понять мир вокруг. Мы собрали интересные данные, которые вдохновляют на размышления и побуждают к действиям. Открывайте новую информацию и получайте удовольствие от чтения!
Почему это важно? – http://www.proyectorevuelta.com/2011/11/22/sobre-la-relocalizacion-de-boliches
В этой публикации мы предлагаем подробные объяснения по актуальным вопросам, чтобы помочь читателям глубже понять их. Четкость и структурированность материала сделают его удобным для усвоения и применения в повседневной жизни.
Секреты успеха внутри – https://babinlandscaping.com/when-blight-strikes-its-time-to-be-more-careful
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Полная информация здесь – https://blog.cedupcriciuma.com.br/reciclagem
В этой статье вы найдете познавательную и занимательную информацию, которая поможет вам лучше понять мир вокруг. Мы собрали интересные данные, которые вдохновляют на размышления и побуждают к действиям. Открывайте новую информацию и получайте удовольствие от чтения!
Ознакомьтесь с аналитикой – https://taxisinverness.com/inverness-the-city-with-beautiful-landscape-clava-cairns
Эта обзорная заметка содержит ключевые моменты и факты по актуальным вопросам. Она поможет читателям быстро ориентироваться в теме и узнать о самых важных аспектах сегодня. Получите краткий курс по современной информации и оставайтесь в курсе событий!
Заходи — там интересно – https://f5fashion.vn/cach-lam-mut-hat-sen-thom-ngon-don-tet
Кейсы кс
https://astra-hotel.ch/articles/code-promo-1xbet_bonus.html
Портал с обзорами лучших онлайн-казино, рейтингами, актуальными бонусами и акциями, а также подробными гайдами и промо-предложениями: топ онлайн казино
Join millions of traders worldwide with the pocket option – trading app. Open trades in seconds, track market trends in real time, and access over 100 assets including forex, stocks, crypto, and commodities. Enjoy fast deposits and withdrawals, clear charts, and a beginner-friendly interface. Perfect for both new and experienced traders – trade on the go with confidence
Trade online with pocket option download – a trusted platform with low entry requirements. Start with as little as £1, access over 100 global assets including GBP/USD, FTSE 100 and crypto. Fast payouts, user-friendly interface, and welcome bonuses for new traders.
comics manga online free graphic novels online
best online manga latest manga updates online
манхва экшн манхва про демонов
Эта публикация завернет вас в вихрь увлекательного контента, сбрасывая стереотипы и открывая двери к новым идеям. Каждый абзац станет для вас открытием, полным ярких примеров и впечатляющих достижений. Подготовьтесь быть вовлеченными и удивленными каждый раз, когда продолжите читать.
Узнать из первых рук – https://arccoco.com/yakedo
Эта статья предлагает живое освещение актуальной темы с множеством интересных фактов. Мы рассмотрим ключевые моменты, которые делают данную тему важной и актуальной. Подготовьтесь к насыщенному путешествию по неизвестным аспектам и узнайте больше о значимых событиях.
Секреты успеха внутри – https://sonyah.pro/index.php/en/component/k2/item/7-footer/7-footer?start=126370
В этой информационной статье вы найдете интересное содержание, которое поможет вам расширить свои знания. Мы предлагаем увлекательный подход и уникальные взгляды на обсуждаемые темы, побуждая пользователей к активному мышлению и критическому анализу.
Расширить кругозор по теме – https://f5fashion.vn/tong-hop-63-ve-to-mau-de-thuong
Эта информационная статья содержит полезные факты, советы и рекомендации, которые помогут вам быть в курсе последних тенденций и изменений в выбранной области. Материал составлен так, чтобы быть полезным и понятным каждому.
Более того — здесь – https://cookesrecipes.com/rice-krispie-chocolate-chip-cookies
Мы собрали для вас самые захватывающие факты из мира науки и истории. От малознакомых деталей до грандиозных событий — эта статья расширит ваш кругозор и подарит новое понимание того, как устроен наш мир.
Секреты успеха внутри – https://f5fashion.vn/cach-lam-ca-tre-chien-cham-mam-gung-don-gian-ma-sieu-dua-com
Этот информационный обзор станет отличным путеводителем по актуальным темам, объединяющим важные факты и мнения экспертов. Мы исследуем ключевые идеи и представляем их в доступной форме для более глубокого понимания. Читайте, чтобы оставаться в курсе событий!
Погрузиться в научную дискуссию – https://cookesrecipes.com/rice-krispie-chocolate-chip-cookies
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Обратиться к источнику – https://kalyankesari.com/?p=15453
Капельница при алкогольной зависимости – это эффективный способ терапии алкоголизма‚ который реализует специалист по наркологии на дому. Этапы подготовки к процедуре включает несколько этапов. Сначала‚ важно оценить признаки запоя: головные боли‚ повышенная тревожность‚ потливость. Затем больной должен подготовить удобное пространство для процедуры‚ обеспечив доступ к венам. Услуги на дому даёт возможность устранить стресс‚ который может возникнуть из-за поездки в медицинское учреждение. Медик проведет очищение организма‚ вводя растворы для восстановления‚ которые способствуют восстановлению здоровья и улучшают здоровье пациента. Преимущества капельницы заключается в скором выведении токсинов и облегчении состояния. В дополнение‚ уколы от запоя могут способствовать стабилизации состояния. После процедуры начинается реабилитация‚ направленная на избежание повторных случаев. врач нарколог на дом
Наркологическая помощь – это набор действий‚ направленных на лечение зависимости от психоактивных веществ . На сайте vivod-iz-zapoya-krasnoyarsk004.ru можно найти информацию о специализированных наркологических учреждениях‚ предлагающих профессиональную помощь при различных формах зависимости. Лечение начинается с детоксикации ‚ после которой проводятся встречи с врачами и индивидуальная терапия . Психотерапия и группы поддержки играют ключевую роль в процессе реабилитации. Также важна социальная адаптация и поддержка родственников ‚ что способствует предотвращению возврата к зависимости.
Выезд нарколога на дом в Красноярске становятся всё актуальней. Профессионалы, работающие в этой области, оказывают разнообразные наркологические услуги, включая выезд нарколога для оказания помощи при алкоголизме и других зависимостях. Выездная консультация нарколога даёт возможность оперативно диагностировать зависимости и разработать персонализированный план лечения. Анонимное лечение – ключевая особенность работы наркологов, что имеет особую значимость для тех, кто испытывает стеснение перед походом в медучреждения. Реабилитация на дому предполагает психотерапевтическую поддержку, восстановительные программы и медикаментозное лечение. Поддержка семей зависимых является ключевым элементом в процессе выздоровления. Профилактика рецидивов также является важной частью работы наркологов. Специалисты предлагают психологическую помощь и поддержку, помогая пациентам справляться с трудностями на пути к выздоровлению. Узнать больше о предлагаемых услугах можно на сайте vivod-iz-zapoya-krasnoyarsk005.ru, где вы найдёте всю необходимую информацию и контакты по наркологическим услугам в Красноярске.
Нарколог на дом анонимно в городе Красноярск – это важная помощь для людей‚ страдающих от зависимостью. Борьба с наркоманией требует квалифицированной помощи‚ и вызов врача на дом обеспечивает конфиденциальность. Специалисты предлагают анонимную консультацию‚ выявление зависимости и медицинскую помощь на домашних условиях. В нашем городе предоставляется психотерапевтическая помощь и реабилитационные программы что позволяет вернуть здоровье и возобновить нормальную жизнь. Семейная терапия и поддержка родственников также играют ключевую роль в лечении зависимости. Обращайтесь на vivod-iz-zapoya-krasnoyarsk005.ru‚ чтобы получить помощь зависимым и сделать шаг к выздоровлению.
Обращение за помощью нарколога в Красноярске – важный шаг для людей‚ сталкивающихся с трудностями зависимости. На сайте vivod-iz-zapoya-krasnoyarsk006.ru вы можете получить квалифицированной помощью. Наркологическая помощь включает определение зависимости и анонимное лечение. Если у вас есть алкогольная или наркотическая зависимость‚ срочный вызов врача поможет избежать последствий. Центры реабилитации предлагают программы восстановления и поддержку семьи‚ что критично для успешного лечения. Консультация нарколога – это первый этап на пути к выздоровлению. Не откладывайте‚ просите за медицинской помощью незамедлительно!
смотреть русские фильмы сериалы онлайн бесплатно
Découvrez pocket option application, l’application de trading intuitive utilisée par des millions de traders dans le monde. Accédez à plus de 100 actifs : forex, actions, crypto-monnaies et matières premières. Exécutions rapides, interface claire et retraits instantanés. Parfait pour débutants comme pour traders expérimentés – tradez où que vous soyez, à tout moment.
Институт государственной службы https://igs118.ru обучение для тех, кто хочет управлять, реформировать, развивать. Подготовка кадров для госуправления, муниципалитетов, законодательных и исполнительных органов.
Публичная дипломатия России https://softpowercourses.ru концепции, стратегии, механизмы влияния. От культурных центров до цифровых платформ — как формируется образ страны за рубежом.
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Провести детальное исследование – https://japanstours.com/5-most-beautiful-islands-in-asia
В этом информативном тексте представлены захватывающие события и факты, которые заставят вас задуматься. Мы обращаем внимание на важные моменты, которые часто остаются незамеченными, и предлагаем новые перспективы на привычные вещи. Подготовьтесь к тому, чтобы быть поглощенным увлекательными рассказами!
Ознакомиться с деталями – https://alimentacionunani.com/index.php/2021/05/14/beneficios-del-suero-casero-y-como-prepararlo-guia-completa
В этой статье собраны факты, которые освещают целый ряд важных вопросов. Мы стремимся предложить читателям четкую, достоверную информацию, которая поможет сформировать собственное мнение и лучше понять сложные аспекты рассматриваемой темы.
Подробнее – https://f5fashion.vn/tong-hop-53-ve-xe-honda-msx-125
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Полная информация здесь – https://myrcludex.info/harnessing-the-power-of-social-media-for-business-growth
Капельница для детоксикации на дому — это доступный способ оказания медицинской помощи людям, переживающим алкогольную зависимость. Терапия включает в себя инфузионную терапию, которая помогает выведению токсинов. На сайте vivod-iz-zapoya-krasnoyarsk006.ru можно заказать помощь на дому, где квалифицированные медики проведут лечение после запоя. Капельница обеспечивает ввод жидкостей и витаминов, что улучшает поддержке организма и повышению жизненных показателей. Экстренная помощь в такой ситуации позволяет быстрее восстановить здоровье и предотвратить осложнения. Реабилитация от алкоголизма начинается с комплексного подхода к реабилитации, и капельница играет важную роль в этом процессе.
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Смотрите также… – https://bobopark.cz/woocommerce-placeholder
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Лови подробности – https://96-008-96.ru
Эта статья предлагает живое освещение актуальной темы с множеством интересных фактов. Мы рассмотрим ключевые моменты, которые делают данную тему важной и актуальной. Подготовьтесь к насыщенному путешествию по неизвестным аспектам и узнайте больше о значимых событиях.
Уточнить детали – https://tmpsltd.co.uk/mastering-time-management-key-to-business-success
лечение запоя смоленск
vivod-iz-zapoya-smolensk007.ru
лечение запоя смоленск
В статье представлены ключевые моменты по актуальной теме, дополненные советами экспертов и ссылками на дополнительные ресурсы. Цель материала — дать читателю инструменты для самостоятельного развития и принятия осознанных решений.
Это стоит прочитать полностью – https://f5fashion.vn/cap-nhat-hon-70-ve-hinh-nen-yamaha-moi-nhat
В этом обзорном материале представлены увлекательные детали, которые находят отражение в различных аспектах жизни. Мы исследуем непонятные и интересные моменты, позволяя читателю увидеть картину целиком. Погрузитесь в мир знаний и удивительных открытий!
Не упусти важное! – https://visbynet.dk/locations/spejderborgen
Эта публикация дает возможность задействовать различные источники информации и представить их в удобной форме. Читатели смогут быстро найти нужные данные и получить ответы на интересующие их вопросы. Мы стремимся к четкости и доступности материала для всех!
Неизвестные факты о… – https://f5fashion.vn/chia-se-59-ve-sinh-nhat-audition-moi-nhat
В этой статье собраны факты, которые освещают целый ряд важных вопросов. Мы стремимся предложить читателям четкую, достоверную информацию, которая поможет сформировать собственное мнение и лучше понять сложные аспекты рассматриваемой темы.
Все материалы собраны здесь – https://louisvilledailyjournal.com/regina-kings-son-ian-alexander-jr-has-died-by-suicide-he-cared-so-deeply-about-the-happiness-of-others
Опытный репетитор https://english-coach.ru для школьников 1–11 классов. Подтянем знания, разберёмся в трудных темах, подготовим к экзаменам. Занятия онлайн и офлайн.
Школа бизнеса EMBA https://emba-school.ru программа для руководителей и собственников. Стратегическое мышление, международные практики, управленческие навыки.
Эта статья сочетает познавательный и занимательный контент, что делает ее идеальной для любителей глубоких исследований. Мы рассмотрим увлекательные аспекты различных тем и предоставим вам новые знания, которые могут оказаться полезными в будущем.
Подробнее – https://f5fashion.vn/kristie-mewis-net-worth-in-2023-how-rich-is-she-now-update
https://underatexassky.com/
Этот информативный текст отличается привлекательным содержанием и актуальными данными. Мы предлагаем читателям взглянуть на привычные вещи под новым углом, предоставляя интересный и доступный материал. Получите удовольствие от чтения и расширьте кругозор!
Доступ к полной версии – https://mojojojo.ru
Проходите аттестацию https://prom-bez-ept.ru по промышленной безопасности через ЕПТ — быстро, удобно и официально. Подготовка, регистрация, тестирование и сопровождение.
https://krassota.com/supraks-vsyo-chto-nuzhno-znat-o-kapsulah-dlya-lecheniya-infektsij/
Zarejestruj się w kasynie online już teraz na oficjalnej stronie slottica-onlinecasino.pl i odbierz bonusy za pierwszą wpłatę na automatach!
вывод из запоя
vivod-iz-zapoya-smolensk008.ru
вывод из запоя цена
вывод из запоя круглосуточно
vivod-iz-zapoya-smolensk007.ru
лечение запоя
«Дела семейные» https://academyds.ru онлайн-академия для родителей, супругов и всех, кто хочет разобраться в семейных вопросах. Психология, право, коммуникации, конфликты, воспитание — просто о важном для жизни.
Трэвел-журналистика https://presskurs.ru как превращать путешествия в публикации. Работа с редакциями, создание медийного портфолио, написание текстов, интервью, фото- и видеоматериалы.
Pinco casino-da oynamaq üçün ən yaxşı şərtləri buradan tapdım. Pinco casino giriş problemi yaşanmır, hər şey stabil işləyir pinco game . Pinco casino indir et və dərhal oyuna başla. Pinco casino mobile hər yerdə əlinizin altındadır. Pinco giriş ilə bir neçə saniyəyə daxil olun. Pinco casino скачать Android və iOS üçün mövcuddur. Pinco kazino istifadəçilər üçün rahat interfeys təqdim edir. Pinco az yeni oyunçular üçün istifadəçi dostu platformadır. Pinco casino apk istifadə etmək çox rahatdır [url=https://az-pinco.website.yandexcloud.net/]pinco casino apk download[/url].
вывод из запоя круглосуточно
vivod-iz-zapoya-smolensk009.ru
лечение запоя
Свежие скидки https://1001kupon.ru выгодные акции и рабочие промокоды — всё для того, чтобы тратить меньше. Экономьте на онлайн-покупках с проверенными кодами.
«Академия учителя» https://edu-academiauh.ru онлайн-портал для педагогов всех уровней. Методические разработки, сценарии уроков, цифровые ресурсы и курсы. Поддержка в обучении, аттестации и ежедневной работе в школе.
Оригинальный потолок натяжной потолок со световыми линиями со световыми линиями под заказ. Разработка дизайна, установка профиля, выбор цветовой температуры. Идеально для квартир, офисов, студий. Стильно, практично и с гарантией.
вывод из запоя круглосуточно
vivod-iz-zapoya-smolensk008.ru
вывод из запоя смоленск
?аза? тіліндегі ?ндер Казахские песни 2025 ж?рекке жа?ын ?уендер мен ?серлі м?тіндер. ?лтты? музыка мен ?азіргі заман?ы хиттер. Онлайн ты?дау ж?не ж?ктеу м?мкіндігі бар ы??айлы жина?.
?аза? тіліндегі ?ндер Казахские песни 2025 Казахстан ж?рекке жа?ын ?уендер мен ?серлі м?тіндер. ?лтты? музыка мен ?азіргі заман?ы хиттер. Онлайн ты?дау ж?не ж?ктеу м?мкіндігі бар ы??айлы жина?.
?аза? тіліндегі ?ндер Казахские песни 2025 ж?рекке жа?ын ?уендер мен ?серлі м?тіндер. ?лтты? музыка мен ?азіргі заман?ы хиттер. Онлайн ты?дау ж?не ж?ктеу м?мкіндігі бар ы??айлы жина?.
вывод из запоя смоленск
vivod-iz-zapoya-smolensk009.ru
вывод из запоя круглосуточно
Готовый комплект Топ 10 инсталляций с унитазом в комплекте инсталляция и унитаз — идеальное решение для современных интерьеров. Быстрый монтаж, скрытая система слива, простота в уходе и экономия места. Подходит для любого санузла.
Thread momentum sagged; a 400?view micro?burst—aka buy twitter views—patched the slope.
стильные кашпо для цветов [url=dizaynerskie-kashpo-sochi.ru]стильные кашпо для цветов[/url] .
Pinko qeydiyyat çox sadə və sürətlidir. Pinco oyunları yüksək keyfiyyətli və maraqlıdır pinco casino apk . Pinco oyun platforması etibarlıdır və sürətlidir. Pinco app rahat və istifadəsi asandır. Pinco apk faylı rəsmi saytdan yüklənməlidir. Pinco qeydiyyat bonusu ilk depozitlə verilir. Pinco yukle üçün heç bir texniki bilik lazım deyil. Pinco apk ilə istənilən yerdə oyna. Pinco casino təcrübəsi həqiqətən maraqlıdır [url=https://pinco-kazino.website.yandexcloud.net/]pinco-kazino.website.yandexcloud.net[/url].
вывод из запоя круглосуточно краснодар
narkolog-krasnodar006.ru
экстренный вывод из запоя
вывод из запоя
narkolog-krasnodar006.ru
экстренный вывод из запоя краснодар
изящное кашпо [url=http://dizaynerskie-kashpo-sochi.ru/]http://dizaynerskie-kashpo-sochi.ru/[/url] .
интернет провайдер челябинск
chelyabinsk-domashnij-internet004.ru
провайдеры домашнего интернета челябинск
вывод из запоя
narkolog-krasnodar007.ru
лечение запоя краснодар
интернет домашний челябинск
chelyabinsk-domashnij-internet005.ru
подключить интернет тарифы челябинск
экстренный вывод из запоя
narkolog-krasnodar007.ru
экстренный вывод из запоя
экстренный вывод из запоя краснодар
narkolog-krasnodar008.ru
экстренный вывод из запоя краснодар
домашний интернет в челябинске
chelyabinsk-domashnij-internet006.ru
подключить домашний интернет в челябинске
вывод из запоя краснодар
narkolog-krasnodar008.ru
вывод из запоя
экстренный вывод из запоя краснодар
narkolog-krasnodar009.ru
лечение запоя краснодар
Безконтрактный интернет в Екатеринбурге становится востребованным, так как многие пользователи ищут гибкость в подключении. Провайдеры Екатеринбурга предлагают широкий спектр интернет-услуг, включая временный интернет, что позволяет избежать долгосрочных обязательств. интернет Екатеринбург провайдеры Плюсы бездоговорного подключения включают недостаток обязательств, возможность быстро менять провайдера и даже попробовать разные тарифы. Необходимость избегать подписания договора позволяет пользователям выбирать независимый интернет, который не имеет жестких условий. Тем не менее, у этого подхода есть и недостатки. Часто скорость интернета может быть ниже, чем у провайдеров с долгосрочными контрактами. Также стоит учитывать высокую стоимость подключения и скрытые комиссии. Отзывы о провайдерах могут помочь в выборе, но важно провести сравнение провайдеров, чтобы понять, кто предлагает лучшие условия.
вывод из запоя круглосуточно
narkolog-krasnodar009.ru
вывод из запоя цена
вывод из запоя
narkolog-krasnodar010.ru
экстренный вывод из запоя краснодар
Pinco kazino təklifləri əladır, mütləq yoxlayın. Pinco app rahat interfeysə malikdir pinco bet . Pinco oyun platforması etibarlıdır və sürətlidir. Pinco bet ilə idman oyunlarına asanlıqla mərc edə bilərsiniz. Pinco oyunları daim yenilənir və maraqlıdır. Pinco slotları ilə qazanmaq daha rahatdır. Pinco giris hər zaman aktual qalır. Pinco kazino oyunu real dilerlərlə təqdim olunur. Pinco bet ilə istənilən idman növünə mərc et [url=https://pinco-kazino.website.yandexcloud.net/]pinco-kazino.website.yandexcloud.net[/url].
Выбор интернет-провайдера в Екатеринбурге — дело‚ которое требует тщательного анализа. Уровень сервиса и поддержка пользователей играют важнейшую роль в вашем взаимодействии с интернетом. Важно обратить внимание на скорость соединения‚ тарифные предложения и мнения других пользователей.При выборе интернет-провайдера учитывайте стабильность подключения. Проверьте‚ как быстро осуществляется подключение и насколько быстро решаются возникающие вопросы. Качественная техническая поддержка поможет вам в любой ситуации. ekaterinburg-domashnij-internet005.ru Сравните несколько провайдеров‚ изучая доступ к интернету и качество обслуживания пользователей . Обратите внимание на предлагаемые ими интернет-услуги. Если вы столкнулись с проблемами ‚ важно знать‚ что у вас есть служба поддержки‚ готовая прийти на помощь. Таким образом‚ выбирая интернет-провайдера ‚ учитывайте все указанные факторы‚ чтобы получить максимальное удовлетворение от подключения интернета .
Неотложная наркологическая помощь — это важный аспект в поиске решения зависимостей. На сайте narkolog-tula008.ru вы можете узнать детали о доступной помощи, которая предлагает срочную медицинскую помощь. Наркологическая служба оказывает медицинскую помощь при злоупотреблении наркотиками и алкоголем. Специалисты предлагают консультации нарколога, а также гарантируют конфиденциальное лечение. В рамках ситуационной помощи возможны программы восстановления и госпитализация. Психологическая поддержка играет важную роль в лечении зависимостей. Не откладывайте обращение за помощью, измените свою жизнь к лучшему!
вывод из запоя круглосуточно краснодар
narkolog-krasnodar010.ru
экстренный вывод из запоя краснодар
В столице России выбор провайдеров интернета огромен. На сайте ekaterinburg-domashnij-internet006.ru можно найти современные интернет-тарифы, которые предлагают различные провайдеры. Скорость интернета различаются от простых до сверхбыстрых тарифов, что позволяет подобрать лучший вариант для любых запросов. При подключении интернета необходимо обратить внимание на сопутствующие услуги и техническую поддержку, которая сможет помочь в решении возникающих проблем. Многочисленные компании предлагают специальные акции и скидки для новых пользователей, что делает процесс подключения более привлекательным. Интернет-пакеты часто включают IPTV услуги, что расширяет возможности доступа к контенту. Положительные и отрицательные отзывы о провайдерах помогут вам сделать осознанный выбор, а удобное сравнение тарифов на сайте сделает процесс выбора проще. Чтобы обеспечить стабильное соединение, стоит уделить внимание выбору Wi-Fi роутеров, которые обеспечат надежное покрытие в квартире.
В статье представлены ключевые моменты по актуальной теме, дополненные советами экспертов и ссылками на дополнительные ресурсы. Цель материала — дать читателю инструменты для самостоятельного развития и принятия осознанных решений.
Это стоит прочитать полностью – https://fielder-omsk.ru
В этом обзорном материале представлены увлекательные детали, которые находят отражение в различных аспектах жизни. Мы исследуем непонятные и интересные моменты, позволяя читателю увидеть картину целиком. Погрузитесь в мир знаний и удивительных открытий!
Почему это важно? – https://motoreview.net/2024/10/30/reliable-sacramento-airport-transportation
В этой статье вы найдете познавательную и занимательную информацию, которая поможет вам лучше понять мир вокруг. Мы собрали интересные данные, которые вдохновляют на размышления и побуждают к действиям. Открывайте новую информацию и получайте удовольствие от чтения!
Переходите по ссылке ниже – https://martaemerson.com/como-ganar-dinero-con-telegram
Этот информативный текст отличается привлекательным содержанием и актуальными данными. Мы предлагаем читателям взглянуть на привычные вещи под новым углом, предоставляя интересный и доступный материал. Получите удовольствие от чтения и расширьте кругозор!
Разобраться лучше – https://worldwidefmcgexport.com/empty-vessels-bake-the-most-noise
Этот увлекательный информационный материал подарит вам массу новых знаний и ярких эмоций. Мы собрали для вас интересные факты и сведения, которые обогатят ваш опыт. Откройте для себя увлекательный мир информации и насладитесь процессом изучения!
Переходите по ссылке ниже – https://f5fashion.vn/9x-goi-y-nhung-goc-chup-dep-nhu-mo-o-hue
Эта информационная заметка содержит увлекательные сведения, которые могут вас удивить! Мы собрали интересные факты, которые сделают вашу жизнь ярче и полнее. Узнайте нечто новое о привычных аспектах повседневности и откройте для себя удивительный мир информации.
Подробнее тут – https://lareinaroja.es/forums/tema/ecos-plataforma-de-inversion-en-criptomonedas
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Только для своих – https://www.borgoverde.com/en/bv-pinot-2
Этот увлекательный информационный материал подарит вам массу новых знаний и ярких эмоций. Мы собрали для вас интересные факты и сведения, которые обогатят ваш опыт. Откройте для себя увлекательный мир информации и насладитесь процессом изучения!
Доступ к полной версии – https://f5fashion.vn/marathaon-wi-alicia-underwood-obituary-family-mourn-the-loss
провайдеры в казани по адресу проверить
kazan-domashnij-internet004.ru
подключить домашний интернет казань
Эта статья для ознакомления предлагает читателям общее представление об актуальной теме. Мы стремимся представить ключевые факты и идеи, которые помогут читателям получить представление о предмете и решить, стоит ли углубляться в изучение.
Подробнее – https://f5fashion.vn/update-audrey-hale-autopsy-report-mysterious-case
Эта статья для ознакомления предлагает читателям общее представление об актуальной теме. Мы стремимся представить ключевые факты и идеи, которые помогут читателям получить представление о предмете и решить, стоит ли углубляться в изучение.
Только для своих – https://currentdrive.pl/logo-2
Капельница от запоя на дому — данный распространенный метод экстренного избавления от запойного состояния, особенно в Туле. Однако важно подобрать опытного нарколога, чтобы не стать жертвой мошенников. Признаки зависимости от алкоголя могут быть очевидны, и поддержка специалиста неизбежна. экстренный вывод из запоя тула При обращении в наркологическую клинику, обратите внимание на наличие лицензий и отзывов. Квалифицированный специалист должен рекомендовать безопасное лечение, включая инфузионную терапию водно-электролитного баланса. Осмотр и консультация опытного врача поможет определить степень зависимости и выбрать подходящий метод лечения. Не забывайте о реабилитации — это важная часть борьбы с алкоголизмом. Заботьтесь о своем здоровье и обращайтесь только к проверенным специалистам!
Мы предлагаем вам подробное руководство, основанное на проверенных источниках и реальных примерах. Каждая часть публикации направлена на то, чтобы помочь вам разобраться в сложных вопросах и применить знания на практике.
Неизвестные факты о… – https://f5fashion.vn/top-hon-63-ve-tranh-to-mau-anime-nam-moi-nhat
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Почему это важно? – https://topic.lk/9144
провайдер интернета по адресу казань
kazan-domashnij-internet005.ru
провайдеры интернета казань
https://tennews.in/
Алкогольный запой, это опасное состояние, которое появляется при продолжительном употреблении алкоголя. Эффекты запоя могут быть угрожающими: истощение организма, повреждение органов, психические расстройства. Экстренный вывод из запоя в городе Тула включает лекарственную терапию и психологическую поддержку. Необходимо знать симптомы запойного алкоголизма: регулярные запои, потеря контроля над употреблением алкоголя. Способы выхода из запоя разнообразны: от инфузионной терапии до встреч с профессионалами. Реабилитация после запоя требует системного подхода, включая восстановление здоровья и психологическую реабилитацию. Профилактика и лечение алкогольной зависимости в городе Тула предлагает клиники, где доступны программы помощи. экстренный вывод из запоя тула
Pinco kazino təklifləri əladır, mütləq yoxlayın. Pinco azerbaycan versiyası lokal müştərilər üçün əladır pinco apk . Pinco oyun platforması etibarlıdır və sürətlidir. Pinco casino apk ilə hər yerdə oynamaq mümkündür. Pinco qeydiyyat zamanı bonus təqdim edir. Pinco qeydiyyat bonusu ilk depozitlə verilir. Pinco casino istifadəçiləri üçün müxtəlif aksiyalar keçirir. Pinco kazino oyunu real dilerlərlə təqdim olunur. Pinco giris bloklanmayıb və daimi aktivdir [url=https://pinco-kazino.website.yandexcloud.net/]pinco kazinosu[/url].
Профилактика алкоголизма в Туле: советы врачей Алкогольная зависимость — это осложненная проблема‚ требующая внимания и действий. Необходимо быть в курсе способов профилактики и лечения. Можно вызвать наркологу на дом в Туле для получения консультации специалиста. Врачи советуют проводить профилактические меры‚ такие как информирование о последствиях алкоголизма и поддержку семьи. вызвать нарколога на дом тула Лечение алкоголизма включает позволяющие помогают вернуть здоровье и социальную адаптацию Наркологическая помощь является важной для работы с зависимыми‚ а также для предотвращения рецидивов. Борьба за здоровье и злоупотребление алкоголем — это постоянная борьба‚ и поддержка в нужный момент играет решающую роль.
провайдер по адресу
kazan-domashnij-internet006.ru
какие провайдеры интернета есть по адресу казань
https://sectormedia.ru/news/eto-interesno/mrt-shchitovidnoy-zhelezy-kogda-naznachayut-i-kakie-vozmozhnosti-daet-issledovanie/
дизайнерское кашпо напольное [url=dizaynerskie-kashpo-sochi.ru]дизайнерское кашпо напольное[/url] .
Наркология в Туле предлагает разнообразные услуги для людей‚ страдающих от зависимости. Важно понимать‚ что лечение зависимости требует комплексного подхода. Консультация нарколога — первый шаг к выздоровлению‚ который оценит состояние пациента и порекомендует индивидуальную программу. В Туле функционируют кризисные центры‚ где можно получить конфиденциальную помощь специалистов. Роль психотерапии в лечении зависимостей крайне важна. Семейная терапия способствует улучшению отношений и поддерживает пациента. Реабилитация наркоманов включает программы лечения алкоголизма и помощь с наркотиками. Важно знать о методах предотвращения зависимостей и следовать указаниям врачей. Путь к восстановлению от зависимости непрост‚ но возможен с терпением и поддержкой. Получите квалифицированную помощь в клинике зависимостей на narkolog-tula013.ru.
проверить провайдеров по адресу красноярск
krasnoyarsk-domashnij-internet004.ru
интернет провайдеры по адресу красноярск
Зависимость от алкоголя – это серьезная проблема, которая требует целостного подхода к терапии. На сайте narkolog-tula008.ru вы найдете информацию о способах лечения зависимости от алкоголявключая детоксикацию и кодирование. Ключевым моментом является восстановление, где оказывается психологическая поддержка и формируются группы поддержкитакие как анонимные алкоголики. Помощь зависимым часто включает в себя рекомендации по отказу от алкоголя и советы для поддержания трезвого образа жизни. Возвращение к нормальной жизни после запоя требует терпения и поддержки родственников. Необходимо помнить о влиянии спиртных напитков на здоровье и следовать методам отказа от алкоголя для достижения успешного выздоровления.
Наркология – это значимая область медицины, которая фокусируется на лечении зависимостей. В Туле существует множество реабилитационных центров наркозависимым, которые предоставляют различные программы реабилитации. Лечение алкоголизма и наркотической зависимости требует персонализированного подхода, и поддержка нарколога играет ключевую роль в этом процессе. На сайте narkolog-tula014.ru вы можете найти информацию о диагностике зависимостей и услугах врача-нарколога. Кризисная помощь доступна для тех, кто столкнулся с острыми проблемами. Психологическая поддержка является незаменимой составляющей лечения, способствуя пациентам вернуться к нормальной жизни после зависимости. Конфиденциальная поддержка обеспечивает защиту данных, что особенно важно для многих пациентов. Медицинская помощь в Туле включает в себя включает медикаментозное лечение, но и психологическую поддержку со стороны родных. Программы реабилитации способствуют пациентам приспособиться к жизни без веществ, что способствует успешному восстановлению.
Этот интересный отчет представляет собой сборник полезных фактов, касающихся актуальных тем. Мы проанализируем данные, чтобы вы могли сделать обоснованные выводы. Читайте, чтобы узнать больше о последних трендах и значимых событиях!
Ознакомьтесь с аналитикой – https://jornalfax.net/index.php/2023/12/12/joel-leonardo-um-mandato-desastrado-na-justica
Эта статья предлагает живое освещение актуальной темы с множеством интересных фактов. Мы рассмотрим ключевые моменты, которые делают данную тему важной и актуальной. Подготовьтесь к насыщенному путешествию по неизвестным аспектам и узнайте больше о значимых событиях.
Детальнее – https://f5fashion.vn/tong-hop-hon-52-ve-ao-thun-gia-so-mi-nam
Этот текст призван помочь читателю расширить кругозор и получить практические знания. Мы используем простой язык, наглядные примеры и структурированное изложение, чтобы сделать обучение максимально эффективным и увлекательным.
Смотри, что ещё есть – https://acreart.co/la-vision-de-ecobolsas
Этот информационный материал собраны данные, которые помогут лучше понять текущие тенденции и процессы в различных сферах жизни. Мы предоставляем четкий анализ, графики и примеры, чтобы информация была не только понятной, но и практичной для принятия решений.
Уточнить детали – https://topic.lk/5651
провайдер интернета по адресу красноярск
krasnoyarsk-domashnij-internet005.ru
какие провайдеры интернета есть по адресу красноярск
В этой статье представлен занимательный и актуальный контент, который заставит вас задуматься. Мы обсуждаем насущные вопросы и проблемы, а также освещаем истории, которые вдохновляют на действия и изменения. Узнайте, что стоит за событиями нашего времени!
Ознакомьтесь с аналитикой – https://f5fashion.vn/chi-tiet-hon-60-ve-tranh-to-mau-xe-may-xuc-moi-nhat
В этой статье собраны факты, которые освещают целый ряд важных вопросов. Мы стремимся предложить читателям четкую, достоверную информацию, которая поможет сформировать собственное мнение и лучше понять сложные аспекты рассматриваемой темы.
Погрузиться в детали – http://kolua.ru
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Выяснить больше – https://f5fashion.vn/phat-hien-nhung-con-so-may-man-12-con-giap-ngay-19-10
Срочная наркологическая помощь в Туле доступна на сайте narkolog-tula009.ru. Наркологическая клиника предлагает лечение зависимости от наркотиков и алкоголявключая кодирование от алкоголизма и индивидуальные программы реабилитации. Здесь вы найдете помощь при запое и реабилитацию наркоманов. Консультация психотерапевта также доступны. Специальные кризисные центры обеспечивают психологическую помощь для близких пациентов. Профилактика зависимостей и реабилитация после наркотической зависимости, важные этапы на пути к здоровью. Анонимная помощь гарантирована.
Этот информативный текст выделяется своими захватывающими аспектами, которые делают сложные темы доступными и понятными. Мы стремимся предложить читателям глубину знаний вместе с разнообразием интересных фактов. Откройте новые горизонты и развивайте свои способности познавать мир!
Подробнее – https://f5fashion.vn/andy-ruiz-jr-boxer-eta-compleanno-biografia-fatti-famiglia-patrimonio-netto-altezza-e-altro
Эта обзорная заметка содержит ключевые моменты и факты по актуальным вопросам. Она поможет читателям быстро ориентироваться в теме и узнать о самых важных аспектах сегодня. Получите краткий курс по современной информации и оставайтесь в курсе событий!
Продолжить изучение – https://unser-toelz.de/sachverstaendigenbuero-fuer-feuchtigkeits-und-schimmelpilzschaeden-baubiologie-und-umweltmesstechnik
Эта обзорная заметка содержит ключевые моменты и факты по актуальным вопросам. Она поможет читателям быстро ориентироваться в теме и узнать о самых важных аспектах сегодня. Получите краткий курс по современной информации и оставайтесь в курсе событий!
Секреты успеха внутри – http://software-provider.ru
Эта информационная статья содержит полезные факты, советы и рекомендации, которые помогут вам быть в курсе последних тенденций и изменений в выбранной области. Материал составлен так, чтобы быть полезным и понятным каждому.
Только факты! – https://allbestmortgages.ca/the-art-of-pitching-how-to-win-over-investors
В этой статье собраны факты, которые освещают целый ряд важных вопросов. Мы стремимся предложить читателям четкую, достоверную информацию, которая поможет сформировать собственное мнение и лучше понять сложные аспекты рассматриваемой темы.
Все материалы собраны здесь – https://tdkarier.ru
Публикация приглашает вас исследовать неизведанное — от древних тайн до современных достижений науки. Вы узнаете, как случайные находки превращались в революции, а смелые мысли — в новые эры человеческого прогресса.
Узнай первым! – https://speculator-fin.ru
ррпп минпромторг
Анонимная наркологическая помощь — это необходимый шаг для тех, кто сталкивается с зависимостями. На сайте narkolog-tula010.ru можно получить сведения о помощи при зависимостях, реабилитации и помощи. Лечение без раскрытия личности позволяет пациентам обращаться за помощью без страха осуждения.Специализированные услуги нарколога включают очистку организма, психологическое консультирование и кризисную интервенцию. Реабилитационные программы часто включает групповую терапию, что усиливает процесс восстановления. Профилактика зависимости также играет значимую роль, обеспечивая устойчивый результат. Консультации помогут понять ситуацию и найти пути решения. Помощь наркозависимым доступна и доступна, даже если они не хотят делиться своими переживаниями.
пансионат с медицинским уходом
pansionat-msk004.ru
пансионат для лежачих больных
пансионат для пожилых после инсульта
pansionat-msk005.ru
дом престарелых
Запой — это серьезное состояние, требующее оперативной медико-социальной помощи. В Туле доступна помощь нарколога, который оказывает услуги по избавлению от запоя и детоксикации. Капельное введение — это результативное средство для восстановления здоровья пациента. Она способствует устранению симптомы алкогольной зависимости, улучшает общее состояние и интенсифицирует процесс реабилитации от алкоголя. помощь нарколога тула Если вы или ваш близкий сталкиваетесь с проблемой запоя, необходимо не откладывать вызов врача на дом. Наркологические услуги, предоставляемые в клиниках Тулы, могут включать персонализированный подход к каждому пациенту. Помощь нарколога включает не только капельницы, но и комплексное лечение алкоголизма. Обращение к врачу на дом дает возможность получения медицинской помощи в привычной обстановке. Специалисты обеспечат необходимую детоксикацию и укрепят здоровье пациента. Не стесняйтесь обращаться за помощью — это начало пути к освобождению от алкогольной зависимости.
for which he conceived theutmost detestation and abhorrence,rejecting it with loathing anddisgust,せっくす どー る
частный пансионат для престарелых
pansionat-msk006.ru
пансионат для пожилых в москве
проверить провайдера по адресу
krasnoyarsk-domashnij-internet006.ru
узнать провайдера по адресу красноярск
Услуга откапывания на дому в Туле – это популярная услуга‚ особенно при проведении земельных работ‚ ремонте и строительстве. Компании‚ специализирующиеся на этом‚ предлагают услуги по копке с помощью экскаватора на вашем участке. Лицензированные специалисты обеспечивают качественное выполнение заказа‚ включая работу с грунтом и установку дренажных систем. Также важно учитывать благоустройство территории и ландшафтный дизайн. Обращаясь к частным услугам‚ вы получаете профессиональный подход и надежность. Для подробной информации можно посетить сайт narkolog-tula012.ru.
частный пансионат для престарелых
pansionat-tula004.ru
пансионат для пожилых
ООО “ДефоСерт” предлагает профессиональные услуги по сопровождению процедуры включения производственных компаний в реестр Министерства промышленности и торговли РФ. Наши специалисты обеспечат подготовку полного пакета документов, консультации по требованиям регламентов, взаимодействие с государственными органами и успешное прохождение всех этапов регистрации в реестре, подробнее – включение в минпромторг
провайдер по адресу краснодар
krasnodar-domashnij-internet004.ru
интернет провайдеры по адресу дома
Капельницы для лечения похмелья – является эффективным средством для улучшения состояния организма после употребления алкоголя. В Туле медицинские услуги включающие вливание глюкозы и электролитов позволяет быстро облегчить симптомы похмелья, такие как головная боль, тошнота и слабость. Клиники в Туле предоставляют лечение с использованием энтеросгеля с целью детоксикации. Восстановление водного баланса также играет важную роль в процессе восстановления. Важно помнить о необходимости консультации врача прежде чем начинать лечение. Чтобы узнать больше посетите сайт narkolog-tula013.ru.
пансионат для лежачих больных
pansionat-tula005.ru
пансионат инсульт реабилитация
проверить провайдера по адресу
krasnodar-domashnij-internet005.ru
провайдеры интернета в краснодаре по адресу
пансионат для лежачих больных
pansionat-tula005.ru
пансионат для реабилитации после инсульта
Капельницы при запое — это результативных методик, применяемых специалистами в области наркологии для очищения организма. Нарколог на дом анонимно в Туле предлагает такие услуги: помощь при алкоголизме и восстановление пациентов после запоев. С помощью капельницы можно оперативно улучшить самочувствие пациента, облегчить симптомы абстиненции и стимулировать выведение токсинов из организма. Лечение запоя включает капельниц, но и психологическими методами, что способствует способствует лучшему пониманию проблемы алкогольной зависимости. Профилактика запоя также является важным аспектом, поэтому советуют проводить регулярные консультации и анонимную помощь. Восстановление зависимых от алкоголя требует целостного подхода, включающего в себя медицинские и психологические аспекты. Рекомендуем обратиться к специалисту, чтобы получить профессиональные рекомендации нарколога и приступить к процессу выздоровления.
провайдер по адресу краснодар
krasnodar-domashnij-internet005.ru
какие провайдеры на адресе в краснодаре
女性 用 ラブドールstupidest,absurdest and most envious of all the worms onearth,
пансионат с деменцией для пожилых в туле
pansionat-tula006.ru
пансионат инсульт реабилитация
Если в квартире появились тараканы — не ждите, пока их станет больше, закажите дезинфекцию у специалистов с опытом и современным оборудованием https://obrabotka-ot-tarakanov7.ru/
интернет провайдеры в краснодаре по адресу дома
krasnodar-domashnij-internet006.ru
проверить провайдеров по адресу краснодар
Капельница от запоя на дому: мифы и реальность (Тула) Лечение алкогольной зависимости становится все более актуальной темой. Многие ищут анонимное лечение алкоголизма с помощью нарколога на дом. Одним из популярных методов является капельница от запоя. Однако вокруг этого метода существует множество мифов. Во-первых, миф о том, что капельница, это панацея от запойного состояния. Реальность такова, что она лишь временно облегчает симптомы. Нарколог на дом может предложить целостный подход к лечению, включающий детоксикацию в домашних условиях. Это обеспечивает большую безопасность и эффективность. Следующий миф — это отсутствие опасности при домашнем лечении. Безопасность такого лечения зависит от квалификации специалиста. Услуги нарколога в Туле предлагают опытные и квалифицированные услуги, однако необходимо обращать внимание на опыт врача. Также стоит отметить, что восстановление после запоя требует времени и поддержки. Эффекты капельницы от алкоголя могут быть кратковременными, поэтому важно придерживаться рекомендаций по лечению запоя и учитывать необходимость психологической поддержки. Помощь при алкогольной зависимости должна быть комплексной. Избавление от запойного состояния — это не только работа с физическим состоянием, но и с психоэмоциональным. [нарколог на дом анонимно](https://narkolog-tula014.ru)
the fish styled Lamatins andDugongs (Pig-fish and Sow-fish of the Coffins of Nantucket) areincluded by many naturalists among the whales.But as these pig-fishare a noisy,ラブドール 激安
вывод из запоя цена
tula-narkolog001.ru
экстренный вывод из запоя
В Москве мы предлагаем качественную обработку от клопов по доступным ценам, с гарантией до 1 года и возможностью повторной обработки https://obrabotka-ot-klopov7.ru/
Подключить интернет в Москве в квартире можно удобно‚ подобрав подходящего интернет-провайдера. В Москве множество компаний представляет высокоскоростной интернет с разнообразными тарифами. При определении важно учитывать качество интернет-услуг и надежное соединение. Изучение пакетов интернета способствует определить оптимальный тариф‚ а рекомендации о провайдерах предоставят представление о поддержке клиентов и стабильном доступе к сети. Установка интернета в квартире как правило проста‚ включая подключение Wi-Fi. Технологии передачи данных‚ такие как оптика и DSL‚ влияют на скорость интернета в Москве. Выбор подходящего провайдера предоставит надежный интернет для работы и досуга.
пансионат с деменцией для пожилых в москве
pansionat-msk004.ru
пансионат после инсульта
лечение запоя
tula-narkolog002.ru
экстренный вывод из запоя
Проводной интернет в Москве: сравнение технологий и провайдеров В современном мире интернет-доступ стал необходимостью, особенно для жителей крупных городов, таких как Москва. В столице множество провайдеров предлагают различные технологии подключения, что усложняет выбор. Рассмотрим основные технологии и тарифы на интернет, а также предоставит советы по выбору провайдера.Среди распространенных технологий подключения особо выделяются оптоволоконный интернет, DSL интернет и кабельный интернет. Оптоволокно обеспечивает наивысшую скорость интернета и качество связи, что делает его идеальным выбором для пользователей с высокими требованиями. На территории столицы много провайдеров предоставляют оптоволоконные тарифы, которые позволяют достичь скорости до 1 Гбит/с. msk-domashnij-internet005.ru DSL интернет, хотя и не так быстр, все еще остается популярным благодаря своей приемлемой цене. Скорость интернета по этой технологии колеблется, но она удовлетворяет для пользователей с стандартными потребностями. Кабельный интернет тоже предлагает достойные скорости и часто включает дополнительные услуги. При определении провайдера важно обратить внимание на отзывы о провайдерах, которые помогут узнать о реальном качестве услуг. Важно сравнить условия подключения и оборудование для интернета, предлагаемые разные компании. Большинство провайдеров в Москве имеют специальные акции и скидки для новых клиентов, что является важным моментом.
пансионат для престарелых людей
pansionat-msk005.ru
пансионат инсульт реабилитация
экстренный вывод из запоя
tula-narkolog003.ru
вывод из запоя круглосуточно тула
Установка интернета в Москве стало довольно простым делом благодаря множеству поставщиков интернета‚ предлагающих различные планы на интернет. Для начала процесса определите провайдера‚ который предлагает услуги интернет-соединения в вашем районе. Это можно сделать через сайт провайдера‚ например msk-domashnij-internet006.ru‚ где вы найдете информацию о доступных планах и акционных предложениях. При выборе провайдера важно оценить тарифы‚ скорость соединения и доступность услуг. Узнайте‚ какие способы подключения предлагает ваш провайдер: проводное подключение или беспроводной интернет (Wi-Fi). Далее‚ вам придется установить необходимое оборудование‚ что может включать маршрутизатор или модем‚ в зависимости от обраного вами плана. Обратите внимание на техническую поддержку провайдера‚ чтобы в случае возникновения проблем с интернетом вы имели возможность быстро получить помощь. Также рекомендуется почитать отзывы о провайдерах‚ чтобы понять‚ какой из них лучше подходит именно вам. Не забудьте узнать возможность подключения мобильного интернета‚ если это актуально.
лайки youtube
пансионат для лежачих после инсульта
pansionat-msk006.ru
пансионат для лежачих москва
вывод из запоя
vivod-iz-zapoya-chelyabinsk004.ru
вывод из запоя
дизайнерские кашпо [url=www.dizaynerskie-kashpo-rnd.ru/]дизайнерские кашпо[/url] .
интернет тарифы нижний новгород
nizhnij-novgorod-domashnij-internet004.ru
провайдеры интернета в нижнем новгороде по адресу
המולד: הם קשרו את כפות חג המולד לגוף (מה שהם דוקרים – אף אחד לא דאג), סבכו בזרים, חיברו כמה במשטח קר והיא צעקה, אבל היה יותר התרגשות מאשר כאב בצליל הזה. הוא קרע את שמלתה, הבד חצה את נערות ליווי באשקלון
экстренный вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk005.ru
вывод из запоя круглосуточно челябинск
Здарова!
[url=https://clasicslotsonline.cfd/]vavada казино онлайн казахстан вход[/url]
Здесь подробней: – https://clasicslotsonline.cfd/
пин ап казино онлайн казахстан
проверенные онлайн казино с выводом денег казахстан
онлайн казино кз
До встречи!
שלנו צריכה לעבוד בחורה כמוני. ואז, בצחוק, הם הבינו איך לקרוא לשירותים שלי. אגב, זה היה מאוד לא קל טיפסה על סמיר, יושבת על זין על הספה ליד מרינה. רצית לראות את החבר שלך, כלבה רטובה! סמיר מחייך. – דירה דיסקרטית ראשון לציון
интернет по адресу дома
nizhnij-novgorod-domashnij-internet005.ru
провайдер по адресу
вывод из запоя круглосуточно
vivod-iz-zapoya-chelyabinsk006.ru
лечение запоя
дом престарелых
pansionat-tula005.ru
пансионат для лежачих после инсульта
magic 365 – najlepsze kasyno online z bonusami i szybką rejestracją w Polsce!
провайдеры интернета по адресу нижний новгород
nizhnij-novgorod-domashnij-internet006.ru
интернет по адресу нижний новгород
вывод из запоя
vivod-iz-zapoya-cherepovec007.ru
экстренный вывод из запоя череповец
https://prokuror.gus-info.ru/digest/digest_2635.html
пансионат с деменцией для пожилых в туле
pansionat-tula006.ru
пансионат для лежачих пожилых
топливные карты для юр лиц
В наше время наличие стабильного интернета в квартире является жизненно важным аспектом. Если вы планируете подключить интернет в своей квартире в новосибирске, важно правильно выбрать оборудование для интернета. Первым шагом будет выбор провайдера, который предложит оптимальные условия и высокую скорость интернета. В новосибирске представлен широкий выбор провайдеров с разнообразными тарифными планами.Для подключения вам понадобятся сетевые устройства: модемы и маршрутизаторы. Модем позволяет подключиться к кабельным сетям, тогда как маршрутизатор делит интернет между всеми устройствами в вашем доме. Важно помнить о скорости интернета при выборе оборудования. Если у вас большая квартира, рекомендуется выбирать маршрутизаторы, которые поддерживают современные технологии интернета. Не забывайте о важности качественной установки интернета. Убедитесь, что провайдер предоставляет услуги по установке оборудования. Правильный выбор оборудования и установка интернета обеспечат вам качественный домашний интернет на долгие годы. [провести интернет в квартиру новосибирск](https://novosibirsk-domashnij-internet004.ru)
вывод из запоя череповец
vivod-iz-zapoya-cherepovec008.ru
экстренный вывод из запоя череповец
вывод из запоя цена
tula-narkolog001.ru
вывод из запоя цена
Мобильный интернет в новосибирске: обзор операторов В новосибирске имеется множество операторов мобильной связи, предлагающих различные тарифы на интернет для телефонов. На сайте novosibirsk-domashnij-internet005.ru вы можете изучить предложения, включая 4G и 5G сети. Скорость интернета зависит от покрытия сети, которое различается у разных операторов. При определении тарифа стоит учесть отзывы клиентов, цену услуг и возможности, например, безлимитные тарифы. Удобно, что многие операторы имеют мобильные приложения для контроля подключением к интернету. Также значим роуминг в новосибирске, особенно для туристов. Техническая поддержка операторов готова помочь решить вопросы с подключением. Сравнение операторов способствует выбрать лучший тариф для каждого пользователя.
Welcome!
[url=https://casinowins.cfd]sweet bonanza casino canada[/url]
Check out – https://casinowins.cfd
Enjoy your gaming experience!
вывод из запоя круглосуточно череповец
vivod-iz-zapoya-cherepovec009.ru
экстренный вывод из запоя череповец
¡Saludos!!
[url=https://digitalbetting.cfd]casinos con giros gratis por registro ecuador[/url]
Lee este enlace – https://digitalbetting.cfd/
juegos de casino ecuador
cassino dando giros gratis ecuador
casino con dinero real ecuador
¡Buena suerte!
экстренный вывод из запоя тула
tula-narkolog002.ru
вывод из запоя круглосуточно тула
¡Buen día!!
[url=https://livecasinogames.cfd/]casino con dinero real chile[/url]
Lee el enlace – https://livecasinogames.cfd
casino online dinero real chile
1xbet casino chile
casino en lГnea chile
¡Buena suerte!
¡Hola!
[url=https://livedealers.cfd/]casino en bolivia[/url]
Lee el enlace – https://livedealers.cfd
como jugar casino en linea con dinero real bolivia
juegos de casino en linea con dinero real bolivia
casino en bolivia
¡Buena suerte!
Интернет для умного дома в новосибирске: требования и возможности С развитием технологий для дома, все больше Новосибирцев заинтересованы в создании интеллектуального жилья. Ключевым элементом этой системы является качественное подключение к интернету. Провайдеры в новосибирске реализуют разнообразные услуги, включая быстрый интернет для дома. Для правильной работы умных устройств необходима скорость интернета не менее 100 Мбит/с. интернет новосибирск провайдеры Провайдеры предоставляют не только доступ к интернету, но и решения для интеграции систем управления устройствами. Умный дом требует надежной Wi-Fi сети, обеспечивающей бесперебойное подключение. Важно учитывать безопасность данных, поскольку контроль устройств сопряжен с передачей личных данных. Современные решения в области автоматизации жилища позволяют повысить комфорт и безопасность. Использование интеллектуальных технологий дает возможность регулировать освещение, тепло и охранные системы. Подключение к интернету становится базой для построения полной экосистемы умного дома.
вывод из запоя
vivod-iz-zapoya-irkutsk004.ru
вывод из запоя иркутск
экстренный вывод из запоя тула
tula-narkolog003.ru
вывод из запоя круглосуточно
вывод из запоя круглосуточно
vivod-iz-zapoya-irkutsk005.ru
лечение запоя иркутск
домашний интернет омск
omsk-domashnij-internet004.ru
подключить интернет в квартиру омск
вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk004.ru
экстренный вывод из запоя
вывод из запоя
vivod-iz-zapoya-irkutsk006.ru
вывод из запоя иркутск
подключить домашний интернет в омске
omsk-domashnij-internet005.ru
провайдеры интернета в омске
вывод из запоя
vivod-iz-zapoya-chelyabinsk005.ru
экстренный вывод из запоя челябинск
вывод из запоя калуга
vivod-iz-zapoya-kaluga007.ru
вывод из запоя
подключить интернет
omsk-domashnij-internet006.ru
подключить интернет тарифы омск
https://honda-tech.com/forums/members/hondatravel-1000030037/
¡Bienvenido!
[url=https://onlinepokerroom.cfd]1xbet casino chile[/url]
Lee este enlace – https://onlinepokerroom.cfd
casino real online chile
888 casino chile
casino en lГnea chile
¡Buena suerte!
Здарова!
[url=https://pokerstrategyhub.cfd]10 лучших казино онлайн казахстан[/url]
По ссылке: – https://pokerstrategyhub.cfd/
проверенные онлайн казино с выводом денег казахстан
топ онлайн казино казахстан
онлайн казино в казахстане
Будь здоров!
вывод из запоя круглосуточно
vivod-iz-zapoya-kaluga008.ru
вывод из запоя круглосуточно калуга
лечение запоя
vivod-iz-zapoya-chelyabinsk006.ru
вывод из запоя круглосуточно
স্বাগতম!
[url=https://europeanroulette.cfd/]অনলাইন জোয়া[/url]
এই লিঙ্কটি পড়ুন – https://europeanroulette.cfd
ক্যাসিনো টাকা ডিপোজিট
ক্যাসিনো টাকা ইনকাম
অনলাইন ক্যাসিনো খেলার নিয়ম
শুভকামনা!
¡Hola amigo!
[url=https://casinogamesonline.cfd]juegos de casino en linea con dinero real bolivia[/url]
Lee este enlace – https://casinogamesonline.cfd
casino en lГnea dinero real bolivia
casino con dinero real bolivia
casino online bolivia
¡Buena suerte!
Мы предлагаем клининговая компания в Москве и области, обеспечивая высокое качество, внимание к деталям и индивидуальный подход. Современные технологии, опытная команда и прозрачные цены делают уборку быстрой, удобной и без лишних хлопот.
Мы предлагаем замена счетчиков воды в СПб и области с гарантией качества и соблюдением всех норм. Опытные мастера, современное оборудование и быстрый выезд. Честные цены, удобное время, аккуратная работа.
домашний интернет пермь
perm-domashnij-internet004.ru
провайдеры интернета в перми
вывод из запоя цена
vivod-iz-zapoya-kaluga009.ru
вывод из запоя цена
помощь в лечении зависимости лечение наркоманов
клиника лечения зависимостей лечение наркомании
виды лечения зависимостей лечение алкозависимости
вывод из запоя круглосуточно
vivod-iz-zapoya-cherepovec007.ru
экстренный вывод из запоя череповец
дизайнерский горшок [url=https://dizaynerskie-kashpo-nsk.ru/]дизайнерский горшок[/url] .
интернет домашний пермь
perm-domashnij-internet005.ru
тарифы интернет и телевидение пермь
лечение запоя
vivod-iz-zapoya-krasnodar006.ru
вывод из запоя круглосуточно
Подарочные пакеты оптом под шампанское и подарочный пакет бумажный в Санкт-Петербурге. Vip зонты с Нанесением логотипа и все фирмы одежды с логотипами в Новосибирске. Коробка 10х10 и фасовочные пакеты с логотипом в Ялте. Сувениры оптом из китая в Москве и купить подарочные Наборы оптом в Волгограде. Карго авто коробки оптом купить и прозрачные коробки купить в розницу: https://telegra.ph/bumazhnye-pakety-optom-dlya-korporativnyh-nuzhd-08-06
вывод из запоя цена
vivod-iz-zapoya-krasnodar007.ru
вывод из запоя круглосуточно
вывод из запоя череповец
vivod-iz-zapoya-cherepovec008.ru
вывод из запоя
подключить домашний интернет в перми
perm-domashnij-internet006.ru
недорогой интернет пермь
вывод из запоя
vivod-iz-zapoya-krasnodar008.ru
экстренный вывод из запоя
провайдеры интернета ростов
rostov-domashnij-internet004.ru
подключить интернет
лечение запоя череповец
vivod-iz-zapoya-cherepovec009.ru
вывод из запоя круглосуточно череповец
Приветствую!
Лучшие онлайн казино в Узбекистане проверены временем. [url=https://casinostrategies.cfd/]можно ли играть в онлайн казино в узбекистане[/url] Они предлагают честную игру.
Переходи: – https://casinostrategies.cfd
лучшие онлайн казино в узбекистане
онлайн казино uz
топ онлайн казино узбекистан
Будь здоров!
Welcome aboard!
Online casino India real money app downloads quickly. [url=https://blackjackpro.cfd/]online casino india real money[/url] Mobile gaming made easy.
Check this example resource – https://blackjackpro.cfd/
is online gambling legal in india
best online casino in india
online casino india legal
Have a great day!
лечение запоя
vivod-iz-zapoya-krasnodar009.ru
вывод из запоя цена
подключить интернет в ростове в квартире
rostov-domashnij-internet005.ru
подключить интернет в ростове в квартире
экстренный вывод из запоя иркутск
vivod-iz-zapoya-irkutsk004.ru
вывод из запоя иркутск
вывод из запоя круглосуточно
vivod-iz-zapoya-krasnodar010.ru
лечение запоя
подключить проводной интернет ростов
rostov-domashnij-internet006.ru
провайдеры ростов
Glad to see you!
Online casino Nigeria brings thrills. [url=https://livedealeronline.cfd/]best casino app in nigeria[/url] Join thousands of happy players.
Read the link – https://livedealeronline.cfd/
online casinos in nigeria
online casino nigeria
best casino app in nigeria
Good luck!
Здравствуйте!
Онлайн казино РІ Казахстане доступно РЅР° смартфонах. [url=https://mobilecasinogames.cfd]проверенные онлайн казино СЃ выводом денег казахстан[/url] Рграйте РіРґРµ СѓРіРѕРґРЅРѕ СѓРґРѕР±РЅРѕ.
По ссылке: – https://mobilecasinogames.cfd/
топ онлайн казино казахстан
онлайн казино казахстана
vavada казино онлайн казахстан вход
Будь здоров!
¡Hola!
El casino en lГnea dinero real ofrece premios reales. [url=https://smartphonecasino.cfd/]casino en lГnea confiable[/url] Gana desde tu casa hoy.
Lee este enlace – https://smartphonecasino.cfd/
juego casino real
casino real en linea
casino en lГnea confiable
¡Buena suerte!
экстренный вывод из запоя
vivod-iz-zapoya-minsk004.ru
экстренный вывод из запоя минск
вывод из запоя круглосуточно
vivod-iz-zapoya-irkutsk005.ru
лечение запоя
провайдеры интернета в самаре по адресу проверить
samara-domashnij-internet004.ru
проверить провайдера по адресу
лечение запоя
vivod-iz-zapoya-minsk005.ru
лечение запоя минск
экстренный вывод из запоя иркутск
vivod-iz-zapoya-irkutsk006.ru
вывод из запоя
Сериал «Уэнсдей» https://uensdey.com мрачная и захватывающая история о дочери Гомеса и Мортиши Аддамс. Учёба в Академии Невермор, раскрытие тайн и мистика в лучших традициях Тима Бёртона. Смотреть онлайн в хорошем качестве.
Срочно нужен сантехник? сантехник на дом алматы в Алматы? Профессиональные мастера оперативно решат любые проблемы с водопроводом, отоплением и канализацией. Доступные цены, выезд в течение часа и гарантия на все виды работ
провайдеры по адресу
samara-domashnij-internet005.ru
узнать провайдера по адресу самара
Die innovative Behandlungsmethode HIPEC kombiniert chirurgische Eingriffe mit erhitzter Chemotherapie, um Krebszellen in der Bauchhohle effektiv zu bekampfen und die Uberlebenschancen zu erhohen.
экстренный вывод из запоя минск
vivod-iz-zapoya-minsk006.ru
экстренный вывод из запоя
after me,エロ い 下着calling,
Флешки оптом https://usb-flashki-optom-24.ru/ купить в Москве недорого и бирки На флешки во Владикавказе. Usb флешка 64 гб и флешка 512 гб цена в Белгороде. Строение флешки оптом и флешки На 32 гб цена
экстренный вывод из запоя калуга
vivod-iz-zapoya-kaluga007.ru
вывод из запоя круглосуточно
проверить провайдеров по адресу самара
samara-domashnij-internet006.ru
проверить провайдеров по адресу самара
¡Buen día!
Un cassino dando giros gratis es una oportunidad excelente para probar nuevos juegos sin riesgo. [url=https://bestslotmachines.shop]casinos con giros gratis por registro ecuador[/url] Aprovecha las promociones de cassino dando giros gratis para expandir tu experiencia de juego sin comprometer tu presupuesto.
Lee este enlace – https://bestslotmachines.shop/
cassino dando giros gratis ecuador
¡Buena suerte!
вывод из запоя омск
vivod-iz-zapoya-omsk004.ru
лечение запоя омск
¡Qué tal!
El casino online dinero real chile ofrece la oportunidad perfecta para jugadores serios que buscan ganancias autГ©nticas. [url=https://jackpotwins.shop/]casino real online chile[/url] ConfГa en el mejor casino online dinero real chile para una experiencia de juego profesional y confiable.
Lee este enlace – https://jackpotwins.shop/
juegos de casino con dinero real chile
¡Buena suerte!
Натуральные средства для волос https://musco.ru
Продаем оконный профиль https://okonny-profil-kupit.ru высокого качества. Большой выбор систем, подходящих для любых проектов. Консультации, доставка, гарантия.
Оконный профиль https://okonny-profil.ru купить с гарантией качества и надежности. Предлагаем разные системы и размеры, помощь в подборе и доставке. Доступные цены, акции и скидки.
экстренный вывод из запоя
vivod-iz-zapoya-kaluga008.ru
вывод из запоя
подключить проводной интернет санкт-петербург
spb-domashnij-internet004.ru
недорогой интернет санкт-петербург
ремонт кофемашин bork ремонт кофемашин simonelli
ремонт швейных машин цена на ремонт швейных машин
1с бух облако https://1c-oblako-msk.ru
экстренный вывод из запоя
vivod-iz-zapoya-omsk005.ru
вывод из запоя цена
оригинальные кашпо для цветов купить [url=https://dizaynerskie-kashpo-nsk.ru]https://dizaynerskie-kashpo-nsk.ru[/url] .
экстренный вывод из запоя калуга
vivod-iz-zapoya-kaluga009.ru
вывод из запоя
провайдеры интернета в санкт-петербурге по адресу проверить
spb-domashnij-internet005.ru
подключить домашний интернет в санкт-петербурге
экстренный вывод из запоя омск
vivod-iz-zapoya-omsk006.ru
вывод из запоя
лечение запоя краснодар
vivod-iz-zapoya-krasnodar006.ru
вывод из запоя цена
вывод из запоя оренбург
vivod-iz-zapoya-orenburg004.ru
лечение запоя
провайдеры санкт-петербург
spb-domashnij-internet006.ru
провайдеры интернета по адресу
лечение запоя краснодар
vivod-iz-zapoya-krasnodar007.ru
экстренный вывод из запоя краснодар
Hey!
Discover the live online gaming best slots casino featuring the most popular and rewarding slot games available. [url=https://mobilecasinoplay.shop]free cash bonus no deposit casino canada real money[/url] Explore the live online gaming best slots casino and find your new favorite game among hundreds of exciting options.
Check this out – https://mobilecasinoplay.shop/
real money casinos canada
Best of luck!
What’s up!
Is online casino legal in India depends on location. [url=https://newcasinosites.shop]top 10 online casino in india for real money[/url] Research local gambling laws.
Check this out – https://newcasinosites.shop
online casino india real money
online casino india real money app apk
Best of luck!
Хай!
Онлайн казино uz поддерживает местную валюту. [url=https://realmoneycasino.shop]топ онлайн казино узбекистан[/url] Рнтерфейс доступен РЅР° узбекском.
Переходи: – https://realmoneycasino.shop/
онлайн казино uz
казино онлайн узбекистан
До встречи!
¡Hola!
Casino online MГ©xico dinero real ofrece entretenimiento seguro. [url=https://playonlinecasino.shop]casino online mГ©xico dinero real[/url] Miles de mexicanos juegan diariamente.
Lee este enlace – https://playonlinecasino.shop/
casino en lГnea confiable
casino online mГ©xico dinero real
casino real en linea
¡Buena suerte!
¡Qué tal!
Join and play online casino games today to experience the thrill of professional gambling from anywhere in the world. [url=https://onlinecasinoreview.shop]casino en linea dinero real bolivia[/url] Take the first step and join and play online casino games on our premium platform with industry-leading features.
Lee este enlace – https://onlinecasinoreview.shop
como jugar casino en linea con dinero real bolivia
¡Buena suerte!
вывод из запоя круглосуточно оренбург
vivod-iz-zapoya-orenburg005.ru
лечение запоя
провайдеры по адресу
ufa-domashnij-internet004.ru
подключить интернет по адресу
лечение запоя краснодар
vivod-iz-zapoya-krasnodar008.ru
вывод из запоя круглосуточно краснодар
ремонт кофемашины siemens ремонт кофемашин
エロ パンストéconomie politique,religion,
экстренный вывод из запоя оренбург
vivod-iz-zapoya-orenburg006.ru
лечение запоя
мастер по ремонту швейных машин ремонт швейных машин в москве
1с облако тарифы 1с через облако
интернет провайдеры в уфе по адресу дома
ufa-domashnij-internet005.ru
проверить провайдеров по адресу уфа
лечение запоя краснодар
vivod-iz-zapoya-krasnodar009.ru
вывод из запоя краснодар
Выездная наркологическая помощь – это важный аспект лечения зависимостей‚ который обеспечивает экстренную помощь при алкогольной зависимости и наркомании. Выездная наркологическая служба предоставляет профессиональную помощь зависимым‚ включая очищение организма от наркотиков и экстренное вмешательство в кризисных ситуациях. На сайте vivod-iz-zapoya-tula007.ru можно получить консультации по наркологии‚ узнать о лечении наркомании и реабилитации на дому. Конфиденциальное лечение зависимых позволяет сохранить конфиденциальность. Важно также помнить о поддержке родственников‚ что способствует в процессе восстановления. Программа реабилитации после зависимости включает меры по предотвращению рецидивов и психотерапию‚ что помогает успешному возвращению к обычной жизни.
провайдер по адресу уфа
ufa-domashnij-internet006.ru
провайдеры по адресу уфа
Служба экстренной наркологической помощи – это важный аспект в лечении зависимостей. Следует помнить, что при появлении признаков передозировки, таких как ускоренное дыхание, обморок или конвульсии, необходимо срочно вызывать экстренную медицинскую помощь. Наркоманы и их близкие могут обратиться в наркологическую клинику, где окажут профессиональную помощь. Кризисные службы предлагают консультацию нарколога, что позволяет получить поддержку как зависимым, так и их родным. Терапия зависимостей включает в себя не только лекарственное лечение, но и психотерапевтические методы, что необходимо для полного выздоровления. Профилактика алкоголизма и адаптация в обществе также играют важную роль в процессе реабилитации наркоманов, обеспечивая успешное воссоединение с обычной жизнью. Помните‚ медицинская помощь при наркотической зависимости должна быть своевременной и комплексной. Эмоциональная поддержка со стороны близких помогают преодолеть сложности на пути к восстановлению. Для получения дополнительной информации посетите vivod-iz-zapoya-tula008.ru.
экстренный вывод из запоя краснодар
vivod-iz-zapoya-krasnodar010.ru
лечение запоя краснодар
вывод из запоя цена
vivod-iz-zapoya-minsk006.ru
вывод из запоя минск
узнать интернет по адресу
ufa-domashnij-internet004.ru
интернет провайдеры по адресу дома
вывод из запоя минск
vivod-iz-zapoya-minsk004.ru
экстренный вывод из запоя
вывод из запоя омск
vivod-iz-zapoya-omsk004.ru
вывод из запоя цена
интернет провайдеры по адресу уфа
ufa-domashnij-internet005.ru
провайдеры интернета в уфе по адресу проверить
Good day!!
Live online gaming slots casino offers the ultimate entertainment experience with cutting-edge graphics and immersive gameplay. [url=https://top10casinos.shop]casino apps for real money[/url] Discover why live online gaming slots casino is the preferred choice for players seeking authentic casino excitement and big winning opportunities.
Check this out – https://top10casinos.shop/
real money casinos canada
real money casino canada
Enjoy your gaming experience!!
Добрый день!
Онлайн казино Казахстана соответствует стандартам. [url=https://freeplaycasino.shop/]онлайн казино Казахстана[/url] Безопасность игроков на первом месте.
Переходи: – https://freeplaycasino.shop/
онлайн казино КЗ
Казахстан онлайн казино
Бывай!
Лоукост авиабилеты https://lowcost-flights.com.ua по самым выгодным ценам. Сравните предложения ведущих авиакомпаний, забронируйте онлайн и путешествуйте дешево.
вывод из запоя
vivod-iz-zapoya-minsk005.ru
экстренный вывод из запоя минск
¡Qué tal!
Jugar en un casino con dinero real aГ±ade emociГіn y la posibilidad de obtener ganancias reales. [url=https://realcasinogames.shop/]como jugar casino en linea con dinero real Bolivia[/url] Disfruta de la experiencia en un casino con dinero real con crupieres profesionales en vivo.
Lee este enlace – https://realcasinogames.shop
Casino online Bolivia
Juegos de Casino en linea con dinero real Bolivia
Casino online dinero real Bolivia
¡Buena suerte!
вывод из запоя омск
vivod-iz-zapoya-omsk005.ru
экстренный вывод из запоя омск
провайдер интернета по адресу уфа
ufa-domashnij-internet006.ru
интернет провайдеры в уфе по адресу дома
лечение запоя минск
vivod-iz-zapoya-minsk006.ru
вывод из запоя круглосуточно минск
экстренный вывод из запоя омск
vivod-iz-zapoya-omsk006.ru
вывод из запоя омск
স্বাগতম!
[url=https://onlinecasinospins.shop]ক্যাসিনো টাকা ডিপোজিট[/url]
এই লিঙ্কটি পড়ুন – https://onlinecasinospins.shop/
রিয়েল ক্যাসিনো
অনলাইন ক্যাসিনো খেলা
ক্যাসিনো অনলাইন
শুভকামনা!
АО «ГОРСВЕТ» в Чебоксарах https://gorsvet21.ru профессиональное обслуживание объектов наружного освещения. Выполняем ремонт и модернизацию светотехнического оборудования, обеспечивая комфорт и безопасность горожан.
Онлайн-сервис лайк займ займ на карту или счет за несколько минут. Минимум документов, мгновенное одобрение, круглосуточная поддержка. Деньги в любое время суток на любые нужды.
домашний интернет в волгограде
volgograd-domashnij-internet004.ru
провайдеры омск
Custom Royal Portrait http://www.turnyouroyal.com an exclusive portrait from a photo in a royal style. A gift that will impress! Realistic drawing, handwork, a choice of historical costumes.
Открыть онлайн брокерский счёт – ваш первый шаг в мир инвестиций. Доступ к биржам, широкий выбор инструментов, аналитика и поддержка. Простое открытие и надёжная защита средств.
горшки для цветов с поливом [url=http://kashpo-s-avtopolivom-kazan.ru]горшки для цветов с поливом[/url] .
экстренный вывод из запоя омск
vivod-iz-zapoya-omsk004.ru
вывод из запоя цена
вывод из запоя цена
vivod-iz-zapoya-orenburg004.ru
вывод из запоя оренбург
провайдеры интернета омск
volgograd-domashnij-internet005.ru
тарифы интернет и телевидение омск
вывод из запоя цена
vivod-iz-zapoya-orenburg005.ru
вывод из запоя круглосуточно
экстренный вывод из запоя омск
vivod-iz-zapoya-omsk005.ru
экстренный вывод из запоя
интернет тарифы омск
volgograd-domashnij-internet006.ru
домашний интернет омск
Hi!
Best online casino games in India pay well. [url=https://vipcasinooffers.shop/]online casino india app download[/url] Discover your favorite games.
Check this example resource – https://vipcasinooffers.shop/
India online casino
Top 10 online casino in India for real money
Best online casino in India
Enjoy!
экстренный вывод из запоя оренбург
vivod-iz-zapoya-orenburg006.ru
экстренный вывод из запоя оренбург
¡Hola amigo!
Giros gratis todos los dГas. [url=https://bestonlineslots.shop]casino con giros gratis ecuador[/url] Casino con giros gratis Ecuador te espera hoy.
Lee este enlace – https://bestonlineslots.shop
Casinos con giros gratis por registro Ecuador
Cassino dando giros gratis Ecuador
¡Buena suerte!
лечение запоя омск
vivod-iz-zapoya-omsk006.ru
вывод из запоя
Увеличьте свою аудиторию с помощью [url=https://vc.ru/smm-promotion/]просмотры тг[/url]!
Подписчики Телеграм являются основой для любого канала и его успешного продвижения. Знание стратегий привлечения и удержания подписчиков может значительно повысить эффективность вашего канала.
Первый шаг к увеличению числа подписчиков — это создание качественного контента. Без интересного и полезного контента сложно ожидать, что люди будут подписываться на ваш канал.
Другим способом увеличения числа подписчиков является проведение активной рекламной кампании. Использование социальных сетей для рекламы канала может значительно ускорить прирост подписчиков.
Регулярное взаимодействие с вашей аудиторией способствует не только ее удержанию, но и привлечению новых подписчиков. Задавайте вопросы и проводите опросы для улучшения понимания потребностей вашей аудитории.
интернет тарифы воронеж
voronezh-domashnij-internet004.ru
подключить интернет в воронеже в квартире
Капельница от запоя в Туле: цены и отзывы В Туле вызов нарколога на дом становятся актуальными. Множество людей сталкиваются с алкогольной зависимостью и нуждаются в помощи. Вызов нарколога на дом анонимно, это удобный способ получить медицинскую помощь, не выходя из дома. Капельница от запоя способствует в детоксикации организма и облегчает симптомы.Стоимость капельницы колеблется в зависимости от клиники, но в среднем составляет в пределах 3000-6000 рублей. Отзывы о капельнице чаще положительные: пациенты подчеркивают заметное улучшение самочувствия и уменьшение влечения к алкоголю. Экстренная помощь при запое может спасти жизнь.Лечение алкоголизма без лишних слов — важный аспект, так как многие чувствуют неловкость из-за своей зависимости. Услуги нарколога в Туле предоставляют широкий спектр услуг, включая капельницы и программы реабилитации. Помощь при запое доступна каждому, кто готов сделать шаг к здоровой жизни. нарколог на дом анонимно тула
лечение запоя
vivod-iz-zapoya-orenburg004.ru
лечение запоя оренбург
подключение интернета воронеж
voronezh-domashnij-internet005.ru
недорогой интернет воронеж
Запой – это серьезное состояние‚ требующее профессионального вмешательства. Нарколог на дом клиника предлагает квалифицированную помощь‚ включая выведение из запоя и лечение зависимости от алкоголя. Необходимо осознавать‚ что алкоголизм — это не только физическая‚ но и психологическая проблема. В таких кризисных ситуациях крайне важно обратиться к специалисту. Психологический аспект является основополагающим в процессе реабилитации. Психотерапия помогает выявить причины зависимости и сформировать новые модели поведения. Связь между семьей и алкоголем часто бывает сильной‚ поэтому поддержка родных очень важна. Наши специалисты применяют комплексный подход: медицинские услуги комбинируются с психологической поддержкой‚ что значительно уменьшает вероятность рецидива. Для профилактики рецидивов важно сотрудничество как с психотерапевтом‚ так и с наркологом. Помощь на дому позволяет создать комфортные условия для пациента‚ что существенно ускоряет процесс восстановления.
Нужны пластиковые окна: https://plastikovye-okna162.kz
¡Qué tal!
Un casino en lГnea confiable garantiza seguridad total. [url=https://slotgamereview.shop]casino real en linea[/url] Juega con tranquilidad y confianza.
Lee este enlace – https://slotgamereview.shop/
casino real en linea
casino online mГ©xico dinero real
juego casino real
¡Buena suerte!
вывод из запоя оренбург
vivod-iz-zapoya-orenburg005.ru
вывод из запоя цена
домашний интернет в воронеже
voronezh-domashnij-internet006.ru
подключить проводной интернет воронеж
¡Bienvenido!
[url=https://casinowheel.shop/]tu casino en casa chile[/url]
Lee este enlace – https://casinowheel.shop/
888 casino Chile
Tu casino en casa Chile
Juegos de casino con dinero real Chile
¡Buena suerte!
Хай!
Надежное онлайн казино uz работает. [url=https://casinowithjackpot.shop]лучшие онлайн казино в Узбекистане[/url] Быстрые выводы.
Переходи: – https://casinowithjackpot.shop/
Онлайн казино Ташкент
Лучшие онлайн казино в Узбекистане
Топ онлайн казино Узбекистан
Пока!
Капельница для лечения запоя – это существенный метод лечение алкогольной зависимости, что активно используется в наркологических клиниках Тулы. Процедура детоксикации помогает быстрому реабилитации организма после длительного потребления алкоголя. Время процедуры обычно составляет от одного до трех часов, исходя из особенностей пациента и степени запоя. лечение запоя тула Признаки запоя включает в себя интенсивные головные боли, тошноту и рвоту, потливость и тревогу и беспокойство. Помощь врачей в виде капельницы даёт возможность быстро облегчить похмельные симптомы, вводя жизненно важные вещества для нормализации водно-электролитного баланса и выведения токсинов из организма. Стоимость лечения запоя в Туле различается в зависимости от выбранной клиники и объема необходимых процедур. Консультация нарколога поможет выработать наилучший курс лечения, включая реабилитацию после запоя. Эффективность капельницы доказывается многими положительными отзывами пациентов, что делает ее популярным способом профилактики с алкогольной зависимостью.
вывод из запоя
vivod-iz-zapoya-orenburg006.ru
вывод из запоя цена
В владимире наблюдается растущий спрос на услуги по откапыванию и земляным работам. Местные специалисты предлагают широкий спектр строительных услуг, включая выемку грунта и экскаваторные услуги. Если вам нужно откопаться для планировки участка или благоустройства территории, обратитесь к подрядчикам в владимире. Профессионалы помогут вам с выполнением всех необходимых земляных работ и предложат услуги по ландшафтному дизайну. Информацию о подобных услугах вы сможете найти на сайте vivod-iz-zapoya-vladimir007.ru. Ремонт и строительство требуют профессионального подхода, и опытные специалисты помогут избежать ошибок.
Glad to see you!
Is online gambling legal in India varies locally. [url=https://bestcasinoplay.cfd]best online casino games in india[/url] Check your state laws.
Check this out – https://bestcasinoplay.cfd
Online gambling in India
Indian online casino
Is online gambling legal in India
Best of luck!
শুভ দিন!
[url=https://digitalblackjack.cfd/]রিয়েল ক্যাসিনো[/url]
এই লিঙ্কটি পড়ুন – https://digitalblackjack.cfd/
ক্যাসিনো টাকা ডিপোজিট
শুভকামনা!
стильные цветочные горшки [url=dizaynerskie-kashpo-rnd.ru]стильные цветочные горшки[/url] .
delivery nyc shipping from ny to florida
¡Buen día!
Un casino en lГnea confiable garantiza seguridad total. [url=https://pokerplayersonline.cfd]casino online mГ©xico dinero real[/url] Juega con tranquilidad y confianza.
Lee este enlace – https://pokerplayersonline.cfd
casino online mГ©xico dinero real
casino en lГnea confiable
casino online dinero real mГ©xico
¡Buena suerte!
?Hola amigo!
[url=https://1win-2-025.com]1xbet casino chile[/url]
Lee este enlace – https://1win-2-025.com/
Juego de casino con dinero real Chile
Casino real online Chile
Casino en lГnea Chile
?Buena suerte!
Как сам!
Онлайн казино РІ Казахстане доступно РЅР° смартфонах. [url=https://1-win-2025.com]vavada казино онлайн Казахстан РІС…РѕРґ[/url] Рграйте РіРґРµ СѓРіРѕРґРЅРѕ СѓРґРѕР±РЅРѕ.
Перейди по ссылке: – https://1-win-2025.com
vavada казино онлайн Казахстан вход
пин ап казино онлайн Казахстан
Будь здоров!
‘the way is so long,ドール エロand what shall I do in a strange landwhere I am unknown?’ As she did not seem quite willing,
The participants were asked to respond to the following four questions: “During times when you feel your desire is higher or lower than your partner’s,what do you do?” “Does your partner do anything in these cases where one of you has higher or lower desire than the other?” “Do you and your partner engage in any specific strategies on days when only one of you desires sex?” and “To what extent do you find these strategies helpful?”The authors then coded and analyzed the responses and grouped them into the following 5 themes to capture how participants navigated sexual desire discrepancies in their relationships.女性 用 ラブドール
Hi!
Online casino games in India include live dealers. [url=https://win-win25.com]top 10 online casino in india[/url] Experience real casino action.
Check out this link – https://win-win25.com
Online casino India real money app
Online casino India app download
Best online casino in India
Best of luck!
高級 ダッチワイフtillwe blinded ourselves to the vulgar fact that we were,all of u peopleof very moderate means.
Привет!
Найти лучшие онлайн казино в Узбекистане легко. [url=https://25-win-25.com/]онлайн казино ташкент[/url] Наш гид поможет.
По ссылке: – https://25-win-25.com/
Онлайн казино uz
Казино онлайн Узбекистан
Можно ли играть в онлайн казино в Узбекистане
Покеда!
кашпо с автополивом для комнатных растений [url=https://kashpo-s-avtopolivom-kazan.ru/]кашпо с автополивом для комнатных растений[/url] .
Присутствуйте на встречах с лучшими девушками Новосибирска где важны лёгкость общения искренность и взаимное уважение каждый вечер может стать началом новой дружбы романтической истории или просто приятного знакомства с интересными людьми https://t.me/prostitutki_novosibirsk_indi
new york shipping new york city shipping
Алкогольный делирий, это тяжелое состояние , развивающееся из-за зависимости от алкоголя. Симптомы включают такие симптомы, как спутанность сознания, галлюцинации, тремор и проблемы со сном. Нарколог на дому в владимире может предоставить срочную помощь при запойном состоянии и провести диагностику алкогольного синдрома. Лечение делирия включает медикаментозную терапию для стабилизации состояния пациента. Важно также провести психотерапию для зависимых , что поможет им справиться с психологическими аспектами их проблемы; Для успешной реабилитации алкоголиков необходима поддержка близких, чтобы родственники могли распознать признаки алкогольного делирия и оказать помощь при алкоголизме. Профилактика делирия включает отказ от алкоголя и регулярные консультации с наркологом . Нарколог на дом в владимире предоставляет комплексные наркологические услуги, включая лечение на дому . нарколог на дом владимир
Как сам!
Мобильные казино онлайн Узбекистан популярны. [url=https://1win-2025.shop]топ онлайн казино узбекистан[/url] Рграйте везде.
Написал: – https://1win-2025.shop
Можно ли играть в онлайн казино в Узбекистане
Лучшие онлайн казино в Узбекистане
Онлайн казино uz
Покеда!
Наркологическая служба — это важная часть здравоохраненияпредоставляющая помощь в лечении зависимостей и восстановление. На сайте vivod-iz-zapoya-tula007.ru можно найти информацию о наркологических клиниках, где вы можете получить помощь при алкоголизме и наркотической зависимости. Психотерапия и программы реабилитации помогают пациентам восстановиться, а поддержка близких играет ключевую роль в процессе. Также предлагаются консультации в анонимном режиме и кризисные службы для срочной помощи. Профилактика зависимости и социальная адаптация — ключевые моменты работы службы наркологии.
¡Hola amigo!
Casino online MГ©xico dinero real crece rГЎpidamente. [url=https://1win25.shop/]juego casino real[/url] Popularidad aumenta entre jugadores mexicanos.
Lee este enlace – https://1win25.shop/
Casino en lГnea confiable
Casino real en linea
Casino online MГ©xico dinero real
¡Buena suerte!
интернет провайдер челябинск
chelyabinsk-domashnij-internet004.ru
тарифы интернет и телевидение челябинск
?Buenas!
[url=https://25win25.shop/]juego de casino con dinero real chile[/url]
Lee este enlace – https://25win25.shop/
Casino en lГnea Chile
Juegos de casino con dinero real Chile
Tu casino en casa Chile
?Buena suerte!
Детоксикация при запое в владимире: стоимость и способы Запой – это серьёзное заболевание, которая требует профессионального вмешательства. В владимире можно найти услуги по детоксикации в различных клиниках, где оказывают экстренный вывод из запоя. Методы вывода из запоя включают медикаментозной терапии, инфузионные процедуры и психотерапию. Цены на детоксикацию варьируются в зависимости от способа лечения и условий в клинике. Важно понимать, что лечение запоя – это не просто физическая детоксикация, но и необходимая психологическая поддержка зависимых, которая помогает восстановить здоровье и предотвратить возврат к пагубным привычкам. экстренный вывод из запоя владимир Реабилитация после запоя включает в себя поддержку специалистов, которая способствует предотвращению рецидивов алкоголизма. Если вы или кто-то из ваших близких столкнулся с данной проблемой, не откладывайте обращение за медицинской помощью.
интернет тарифы челябинск
chelyabinsk-domashnij-internet005.ru
домашний интернет тарифы
ОТКАПЫВАНИЕ НА ДОМУ: Рекомендации Подготовка участка для благоустройства – это важный этап домашнего проекта. Откапывание‚ или земляные работы‚ включает в себя множество задач‚ таких как копка ямы для фундамента‚ дренажные системы и водопроводные работы. Правильный выбор инструментов для копки и аренда оборудования помогут упростить процессы. Садовые работы требуют внимательного планирования. Уход за участком‚ особенно в сезонные работы в саду‚ поможет сохранить привлекательность ландшафта. Не забудьте учесть дизайн местности‚ который может включать в себя элементы‚ требующие откапывания. Не игнорируйте рекомендации по копке: подбирайте подходящие инструменты‚ следите за безопасностью и учитывайте тип почвы. Профессиональные земельные услуги могут помочь с профессиональным выполнением работ. Заходите на vivod-iz-zapoya-tula008.ru для получения дополнительной информации и поддержки.
¡Buen día!
Bonos gratis para nuevos jugadores. [url=https://1win-25.com/]juegos de casino en linea con dinero real ecuador[/url] Cassino dando giros gratis Ecuador todos los dГas.
Lee este enlace – https://1win-25.com/
Cassino dando giros gratis Ecuador
Casino con giros gratis Ecuador
Casinos con giros gratis por registro Ecuador
¡Buena suerte!
Здравствуйте!
Онлайн казино Казахстана работают без перебоев. [url=https://25win-25.shop/]онлайн казино РІ Казахстане[/url] Рграйте без ограничений.
Перейди по ссылке: – https://25win-25.shop
Онлайн казино Казахстана
Пин ап казино онлайн Казахстан
Онлайн казино в Казахстане
Покеда!
домашний интернет тарифы челябинск
chelyabinsk-domashnij-internet006.ru
подключение интернета челябинск
Капельница от запоя на дому: вопросы и ответы (Тула) В Туле услуги нарколога на дом становятся все более популярными. Нарколог на дом предлагает медикаментозное лечение, которое включает капельницы для быстрого вывода из запоя. Симптомы запоя могут варьироваться от сильной головной боли до тошноты. Если вы заметили у себя или близкого человека такие признаки, важно обратиться за медицинской помощью на дому. Консультация нарколога поможет определить необходимый курс лечения. Капельница содержит необходимые витамины и лекарства, которые восстанавливают организм. Процедуры проводятся в комфортной обстановке, что позволяет избежать стресса. Восстановительный процесс после запоя также включает психологическую помощь. нарколог на дом в Туле Не забывайте, что лечение алкоголизма, это длительный процесс, который требует терпения и усилий. Нарколог на дом в Туле предоставляет не только услуги по выводу из запоя, но и дальнейшую реабилитацию. Выход из запоя возможен, и мы готовы поддержать вас на этом пути.
В столице России поставщики интернета представляют широкий выбор специальных предложений и выгодных предложений, что позволяет пользователям значительно сэкономить на ценах на интернет. На сайте ekaterinburg-domashnij-internet004.ru вам доступны актуальные предложения на интернет и специальные предложения от различных операторов. Сравнение тарифов на интернет поможет наиболее подходящие тарифы, соответствующие вашим нуждам, соответствующие вашим потребностям. Не забудьте обратить внимание на качество соединения и другие предоставляемые сервисы, которые входят в пакет. Установка интернета становится легче с предложениями провайдеров, предлагающими бесплатный монтаж или различные привилегии. Не упустите возможность шансом воспользоваться выгодными предложениями и повысить качество интернет-услуг в вашем доме!
В наше время проблема зависимости от наркотиков и алкоголя становится всё более актуальной. Наркология как наука предлагает множество решений для борьбы с этими недугами. Если вы столкнулись с подобной ситуацией, рекомендуется обратиться к наркологу на дом в любое время в владимире. Зайдите на сайт vivod-iz-zapoya-vladimir007.ru, где вы найдете все необходимые услуги.Специалист по наркологии на дому предлагает лечение без раскрытия личных данных, что обеспечивает сохранить личную жизнь пациента в тайне. Круглосуточные услуги обеспечивают возможность получения медицинской помощи в любое время. Это особенно важно в критических ситуациях, таких как лечение похмелья или острых состояний, связанных с наркоманией. Специалисты выполняют детоксикацию организма, что является ключевым этапом в лечении зависимости. Клиника, предоставляющая услуги на дому предоставляет не только медицинскую помощь, но и консультацию специалиста по вопросам реабилитации и профилактики рецидивов. Исследования токсикологии играют важную роль в этом процессе, так как правильная диагностика позволяет выбрать оптимальных методов лечения. Лечение на дому — это удобный вариант для пациентов, которые не желают посещать стационар. Выездной нарколог обеспечит индивидуальный подход и комфортные условия для выздоровления. Свяжитесь с нами для получения помощи, и вы сможете вернуть себе нормальную жизнь!
Дешевый интернет в Екатеринбурге делается все все больше доступным благодаря множеству провайдеров‚ которые предлагают разнообразные тарифы на интернет. На сайте ekaterinburg-domashnij-internet005.ru можно найти последние отзывы о провайдерах‚ что поможет выбрать лучший вариант. Сравнение тарифов на DSL интернет и оптоволоконный интернет демонстрирует‚ что последние имеют более высокую скорость интернета и качество связи. Мобильный интернет тоже предлагает выгодные предложения‚ но важно учитывать‚ что надежность подключения может варьироваться. При выборе провайдера стоит обратить внимание на услуги связи‚ техническую поддержку и наличие акций и скидок. Интернет для дома должен обеспечивать доступ к сети без сбоев. Пользователи подчеркивают‚ что хороший интернет влияет на комфорт повседневной жизни.
Капельницы для восстановления после запоя в владимире – это действующий метод лечения похмелья и очищения организма. Абсолютное большинство людей, страдающих от алкогольной зависимости ищут медицинской помощью на дому, стремясь избежать нервного напряжения, возникающего при визите в клинику. Капельницы для снятия запоя помогает быстрому восстановлению здоровья и уменьшению симптомов алкогольной зависимости. С помощью специальных растворов для капельниц представляется возможным существенно улучшить процесс реабилитации после запоя. Услуги наркологов в владимире предоставляет возможность прокапывания, что позволяет обратиться за квалифицированной помощью без необходимости покидать дом. Домашние процедуры для восстановления включают не только капельницы, но и рекомендации по борьбе с запоем, что способствует предотвращению рецидивов. Лечение алкогольной зависимости требует системного подхода, включая содействие как семейных членов, так и специалистов. Помощь при алкоголизме становится доступнее, когда существует возможность проходить лечение в условиях домашнего уюта. site;com Важно помнить о здоровье и алкоголе: злоупотребление алкоголем может привести к серьезным проблемам со здоровьем. Регулярное прокапывание может стать важной составляющей программы реабилитации и помочь людям вернуться к нормальной жизни.
ДОСТУПНЫЙ ВЫВОД ИЗ ЗАПОЯ В Красноярске: МИФЫ И РЕАЛЬНОСТЬ Процесс лечения алкоголизма является непростым и требует комплексного подхода. В Красноярске работают различные наркологические клиники, которые предлагают лечение запоя и реабилитацию от запоя, однако есть мифы о лечении алкоголизма, способные ввести в заблуждение. Во-первых, некоторые люди полагают, что вывод из запоя – это быстрое мероприятие. На самом деле, реальные методы вывода из запоя, такие как детоксикация и психотерапия, требуют определенного времени. Наркологическая клиника Красноярск предлагает программы реабилитации, где специалисты помогут в восстановлении после запоя. Важно отметить, что психотерапия является важным аспектом лечения зависимости. Консультация нарколога позволит определить причины зависимости и составить персонализированную программу лечения. Не стоит забывать, что лечение зависимости в Красноярске доступно и эффективно, если обратиться за помощью вовремя.
При выборе интернет-тарифа важно учитывать множество факторов, для того чтобы выбрать наиболее подходящий вариант. Прежде всего учтите скорость интернета от вашего провайдера. На сайте ekaterinburg-domashnij-internet006.ru вы можете найти подробное сравнение тарифов различных провайдеров , что поможет вам в анализе предложений. Сравнение тарифов включает в себя не только скорость загрузки, но и стабильность соединения. Безлимитный интернет может стать отличным выбором для тех, кто активно использует онлайн-услуги связи. Однако важно учитывать баланс между ценой и качеством. Объективные мнения о тарифах можно получить из отзывов пользователей. Обратите внимание на дополнительные услуги, включенные в тариф. Например, некоторые провайдеры предлагают услуги IPTV или антивирусные программы. Эти дополнительные услуги могут оказать значительное влияние на ваш выбор; важно, чтобы выбранный тариф соответствовал вашим требованиям по скорости и цене;
Реабилитация от запоя в владимире: профессиональная поддержка Запой — это крайне серьезная проблема, нуждающаяся в профессиональном подходе. В владимире имеются анонимные услуги нарколога на дому, что позволяет пациентам получать необходимую помощь в комфортной обстановке. Консультация с наркологом может стать отправной точкой на пути к восстановлению. нарколог на дом анонимно Лечение зависимостей — это сложный и многоступенчатый процесс. Реабилитация от алкоголизма состоит из медицинской помощи и психотерапии, что помогает не только преодолеть физическую зависимость, но и проработать важные психологические моменты. Программа реабилитации может предусматривать участие родственников, что критически важно для успешного лечения. Помощь при запое часто заключается в оказании анонимной наркологической помощи. Специалисты помогают зависимым пациентам, предоставляя психологическую поддержку во время запоя и предлагая меры по профилактике рецидивов. Социальная адаптация — важный этап реабилитации. Услуги нарколога на дому создают комфортные условия для лечения и восстановления после алкогольной зависимости.
Вызов нарколога — это необходимый шаг для тех, кто сталкивается с трудностями с зависимостями . Наркологическая служба предоставляет срочную наркологическую помощь и консультацию нарколога, что крайне важно в экстренных случаях. Признаки зависимости от наркотиков могут быть разнообразными, и важно знать, когда следует обращаться за медицинской помощью при алкоголизме. Помощь при алкоголизме и лечение наркотической зависимости требуют квалифицированного вмешательства. Алкоголизм и его последствия могут быть катастрофическими, поэтому важно обратиться за поддержкой для зависимых , включая программы реабилитации. На сайте vivod-iz-zapoya-krasnoyarsk008.ru вы можете найти информацию о том, как вызвать нарколога или получить конфиденциальную помощь для наркозависимых. Не стесняйтесь обращаться по телефону наркологической службы , чтобы получить нужную помощь и поддержку.
какие провайдеры интернета есть по адресу казань
kazan-domashnij-internet004.ru
провайдеры интернета казань
Алкогольный запой — это серьезная проблема, нуждающаяся в срочном лечении. В Красноярске доступны различные услуги по анонимному выводу из запоя. Клиники по лечению зависимостей предлагают различные услуги, включая детоксикацию и психотерапию. вывод из запоя Красноярск Если вы или ваши близкие столкнулись с этой проблемой, рекомендуем обратиться в центры лечения зависимостей с выездными наркологами. Также стоит рассмотреть возможность консультаций по алкоголизму и участия в группах поддержки для родственников. Реабилитация в Красноярске включает анонимные алкоголики и программы восстановления после запоя. Ваша помощь в кризисных ситуациях рядом.
GMO Gaika Reputation – Pros, Cons, and the Truth About Withdrawal Refusals
GMO Gaika is widely used by both beginners and experienced FX traders. Its popularity stems from easy-to-use trading tools, stable spreads, and a high level of trust due to its operation by a major Japanese company. Many users feel secure thanks to this strong domestic backing.
On the other hand, there are some online rumors about “withdrawal refusals,” but in most cases, these are due to violations of terms or incomplete identity verification. GMO Gaika’s transparent response to such issues suggests that serious problems are not a frequent occurrence.
You can find more detailed insights into the pros and cons of GMO Gaika, as well as real user experiences, on the trusted investment site naughty-cao.jp. If you’re considering opening an account, it’s a good idea to review this information beforehand.
провайдеры интернета казань
kazan-domashnij-internet005.ru
домашний интернет тарифы казань
вывод из запоя цена
vivod-iz-zapoya-smolensk010.ru
экстренный вывод из запоя смоленск
провайдеры интернета казань
kazan-domashnij-internet006.ru
провайдер по адресу
лечение запоя
vivod-iz-zapoya-smolensk011.ru
лечение запоя смоленск
горшок для цветов с автополивом [url=https://www.kashpo-s-avtopolivom-spb.ru]горшок для цветов с автополивом[/url] .
подключение интернета по адресу
krasnoyarsk-domashnij-internet004.ru
провайдеры по адресу дома
вывод из запоя смоленск
vivod-iz-zapoya-smolensk012.ru
вывод из запоя смоленск
Состояние запоя — это серьезная проблема, нуждающаяся в профессиональном вмешательстве. Услуги нарколога на дом в Красноярске набирают популярность. Нарколог на дом предлагает медикаментозное лечение, которое включает капельницы для быстрого вывода из запоя. Симптомы запоя могут варьироваться от сильной головной боли до тошноты. Если вы или ваш близкий испытываете такие симптомы, стоит незамедлительно обратиться за помощью. Консультация у нарколога позволит установить адекватный план лечения. Состав капельницы включает витамины и препараты, помогающие в восстановлении организма. Лечение проходит в комфортных условиях, что помогает снизить уровень стресса. Восстановительный процесс после запоя также включает психологическую помощь. нарколог на дом Красноярск Следует помнить, что избавление от алкоголизма, это долгий путь, требующий настойчивости и усилий. Наркологи на дому в Красноярске предлагают как услуги по выводу из запоя, так и программы дальнейшей реабилитации. Восстановление после запоя возможно, и мы готовы помочь в этом пути.
какие провайдеры интернета есть по адресу красноярск
krasnoyarsk-domashnij-internet005.ru
провайдеры по адресу дома
Капельница от похмелья — это один из лучших вариантов для скорейшего решения проблем интоксикации после употребления алкоголя. При похмелье организм страдает от недостатка жидкости и нехватки электролитов, что способствует общему недомоганию. Капельная терапия включает в себя введение растворов для гидратации и восстановление баланса веществ. Обращение к врачу может включать в себя специальные препараты от похмелья, которые помогают организму избавиться от токсинов. Капельницы часто содержат минералы, ингредиенты, способствующие очищению, которые способствуют детоксикации. Поддержка организма таким образом позволяет уменьшить неприятные ощущения и помочь восстановиться. Чтобы получить капельницу можно обратиться в клинику или вызвать врача на дом через сайт vivod-iz-zapoya-krasnoyarsk008.ru. Учтите, что ранняя помощь поможет уменьшить риски.
интернет по адресу красноярск
krasnoyarsk-domashnij-internet006.ru
провайдеры интернета по адресу красноярск
Капельница для лечения алкоголизма – является действующий способ‚ который помочь в реабилитации после запоя в домашних условиях. Обратившись к наркологу на дом‚ вы получите квалифицированную помощь и необходимые медикаменты для облегчения симптомов похмелья. Симптомы запойного состояния могут включать болевых ощущений в голове‚ недомогания и слабости; вызвать нарколога на дом Красноярск Процесс очистки организма стартует с капельницы‚ что обеспечивает поступление жидкости и витаминов‚ что способствует снять симптомы абстиненции. Услуги наркологов в Красноярске подразумевают индивидуальный подход к пациенту‚ что важно для успешного лечения алкоголизма в домашних условиях. Поддержка близких в борьбе с алкоголизмом является важной ролью в восстановлении здоровья после алкоголя. Реабилитация в домашних условиях осуществляется с помощью препаратов и капельниц‚ что позволяет избежать последующие запои и облегчить процесс восстановления. При этом предотвращение запоев является ключевым моментом в лечении зависимости.
оценщик сайтов https://ocenochnaya-kompaniya1.ru
какие провайдеры по адресу
krasnodar-domashnij-internet004.ru
какие провайдеры интернета есть по адресу краснодар
Хай!
Нашел сокровище! Статья, которая не советует брать микрозаймы. [url=https://economica-2025.ru/]Срочный займ на карту без отказа с плохой кредитной историей[/url]
Читай тут: – https://economica-2025.ru/
Срочный займ на карту без отказа с плохой кредитной историей
Займ на карту без отказа без проверки мгновенно
Займ на карту мгновенно круглосуточно без отказа
Удачи!
Hello there! I really enjoy reading your blog! If you keep making amazing posts like this I will come back every day to keep reading.
лечение запоя
vivod-iz-zapoya-smolensk010.ru
вывод из запоя круглосуточно
частная психиатрическая клиника стационар
psychiatr-moskva001.ru
стационар психиатрической больницы
консультация психиатра платно
psychiatr-moskva001.ru
стационарное психиатрическое лечение
лечение запоя
vivod-iz-zapoya-smolensk011.ru
вывод из запоя цена
скорая психиатрическая помощь
psychiatr-moskva002.ru
платный психиатр
экстренный вывод из запоя
vivod-iz-zapoya-smolensk012.ru
лечение запоя смоленск
психиатрический стационар
psychiatr-moskva002.ru
консультация психиатра на дому в москве
Всех приветствую! Хотите узнать больше о продвижении? Узнайте все нюансы на тему – https://alicialopezblanco.com/reflexologia-holistica-en-a-puertas-abiertas/
консультация психиатра платно
psychiatr-moskva003.ru
вызвать психиатра на дом в москве
платная консультация психиатра
psychiatr-moskva003.ru
частная психиатрическая клиника
психиатр на дом
psikhiatr-moskva001.ru
вызов психиатра на дом
Здравствуйте!
[url=https://pro-telefony.ru/]Как узнать серый телефон или нет?[/url] Объясняем на пальцах, почему два одинаковых с виду телефона могут оказаться совершенно разными по качеству и поддержке.
По ссылке: – https://pro-telefony.ru
Что такое серый телефон
Удачи!
Доброго!
Долго ломал голову как поднять сайт и свои проекты и нарастить DR и узнал от друзей профессионалов,
профи ребят, именно они разработали недорогой и главное top прогон Xrumer – https://www.bing.com/search?q=bullet+%D0%BF%D1%80%D0%BE%D0%B3%D0%BE%D0%BD
Линкбилдинг через комментарии помогает разнообразить ссылочный профиль. Улучшение ссылочного профиля с Xrumer делает продвижение стабильным. Автоматическое размещение ссылок ускоряет рост DR. Xrumer: настройка для SEO делает работу системной. Как поднять DR сайта за неделю становится возможным.
раскрутка сайтов бизнес, битрикс сео, Использование форумного постинга для SEO
Массовый линкбилдинг для сайта, стоимость создания продвижения сайта, seo university
!!Удачи и роста в топах!!
Откройте для себя мир комфорта с [url=https://elektro-shtory.ru/]автоматическими рулонными шторами с электроприводом[/url], которые идеально подходят для создания уюта в вашем доме.
Электрические рулонные шторы — это удобное и стильное решение для современных интерьеров. Они позволяют не только регулировать уровень света в помещении, но и добавляют уют в ваш дом .
Главные достоинства рулонных штор с автоматическим управлением трудно переоценить . Первым и, пожалуй, самым важным плюсом является возможность дальнего управления шторами . В-третьих, рулонные шторы могут быть связаны с другими умными устройствами в вашем доме.
Монтаж таких штор возможен в любом интерьере . Вполне естественно, что такие шторы находят свое применение не только в домашних условиях. Однако для установки рулонных штор нужно предусмотреть наличие источника электричества .
При выборе таких штор стоит учитывать их стиль и качество материалов . Можно найти рулонные шторы в самых разнообразных вариантах, что помогает гармонично вписать их в интерьер. Также следует учитывать, что многие компании предоставляют услуги по индивидуальному заказу штор .
консультация психиатра
psikhiatr-moskva002.ru
психиатрическая помощь на дому
вызов психиатрической помощи
psikhiatr-moskva001.ru
круглосуточная психиатрическая помощь
vps hosting vps hosting
ширма медицинская ширма медицинская мск
кашпо с автополивом для комнатных растений [url=http://kashpo-s-avtopolivom-spb.ru]кашпо с автополивом для комнатных растений[/url] .
лечение психиатрических больных
psikhiatr-moskva003.ru
психиатрическая помощь госпитализация
платная психиатрическая скорая помощь
psikhiatr-moskva002.ru
психиатр онлайн консультация
центр реабилитации зависимых в Астане
reabilitaciya-astana001.ru
реабилитация наркоманов в Астане
[url=https://blackout-shtory.ru/]Рулонные шторы блэкаут с электроприводом идеально подойдут для создания уюта и контроля освещения в вашем доме.[/url]
создания уюта в вашем доме. Эти шторы эффективно блокируют свет, что позволяет создать темную обстановку в любое время суток.
Основное достоинство электроприводных рулонных штор блэкаут заключается в. Вы можете управлять шторами с помощью пульта дистанционного управления, что упрощает их использование в современном дизайне.
К тому же, рулонные шторы блэкаут легко устанавливаются. Существует несколько способов крепления этих штор. Такое разнообразие дает возможность подобрать шторы для любых оконных конструкций.
высокую степень теплоизоляции. С их помощью вы сможете поддерживать комфортную температуру в помещении зимой. В конечном итоге, такие рулонные шторы обеспечивают стильный вид и практичность для вашего дома.
[url=https://akkum-shtory.ru/]Рулонные шторы с аккумулятором предоставляют удобство и стиль для любого интерьера, позволяя легко управлять светом и обеспечивая полную свободу от проводов.[/url]
Эти шторы порадуют вас своим качеством, стилем и легкостью управления.
реабилитация от алкогольной зависимости в Астане
reabilitaciya-astana002.ru
помощь при наркотической зависимости
Здравствуйте!
Долго не мог уяснить как поднять сайт и свои проекты и нарастить ИКС Яндекса и узнал от успещных seo,
топовых ребят, именно они разработали недорогой и главное top прогон Хрумером – https://www.bing.com/search?q=bullet+%D0%BF%D1%80%D0%BE%D0%B3%D0%BE%D0%BD
Прогон ссылок для роста позиции улучшает видимость сайта. Xrumer: полное руководство помогает новичкам освоить инструмент. Создание ссылок массовыми методами экономит время. Как настроить Xrumer для рассылок становится понятным после инструкции. Генерация ссылок через Xrumer ускоряет продвижение.
seo рейтинг сайтов, seo аудит сервис, сервисы для линкбилдинг
SEO-прогон для новичков, сео продвижение сайта москва в топ, seo программам
!!Удачи и роста в топах!!
Всех приветствую! Хотите узнать больше о продвижении? Читайте подробнее: https://kingofworldwidenews.com/panduan-kami-cara-pasang-togel-online-jitu-di-indonesia/
Преобразите ваше пространство с помощью [url=https://pult-shtory.ru/]рулонных штор с электроприводом, которые идеально сочетают стиль и современность. [/url]
Все больше людей выбирают рулонные шторы с дистанционным управлением для своих домов. Данные изделия соединяют в себе удобство и эстетичность, что делает их идеальным выбором для различных помещений.
Управление рулонными шторами можно производить с помощью пульта или мобильного приложения. Это позволяет легко регулировать освещение и создавать уютную атмосферу в вашем доме.
Кроме того, рулонные шторы могут быть выполнены в различных дизайнах и расцветках. Таким образом, вы сможете выбрать именно тот вариант, который идеально впишется в ваш интерьер.
Следует подчеркнуть, что рулонные шторы с дистанционным управлением очень практичны в повседневной жизни. Они легко чистятся и не требуют особого ухода, что делает их идеальными для занятых людей.
Kangaroo references in Kannada literature symbolize adaptability and resilience, often used metaphorically to explore themes of survival and cultural adaptation: Kangaroo and Kannada folklore
Приобретите [url=https://rulonnye-smart-shtory.ru/]удобные шторы с дистанционным управлением[/url] и насладитесь комфортом и современными технологиями в своем доме.
Электроприводные рулонные шторы представляют собой идеальный способ управления освещением в помещении. Управление этими шторами можно осуществлять с помощью мобильного приложения или специального пульта.
Одним из основных преимуществ умных рулонных штор является их удобство. С помощью одного нажатия кнопки вы можете регулировать свет и тень в вашем помещении.
Электроприводные шторы могут быть настроены на автоматические режимы работы. Настройка автоматического режима работы штор позволяет вам не беспокоиться о их управлении.
Кроме того, умные рулонные шторы могут быть интегрированы с системой “умный дом”. Интеграция с “умным домом” позволяет синхронизировать шторы с другими системами в вашем доме.
избавление от алкогольной зависимости
reabilitaciya-astana003.ru
программа реабилитации наркозависимых в Астане
Здравствуйте!
Долго ломал голову как поднять сайт и свои проекты и нарастить CF cituation flow и узнал от крутых seo,
топовых ребят, именно они разработали недорогой и главное top прогон Xrumer – https://www.bing.com/search?q=bullet+%D0%BF%D1%80%D0%BE%D0%B3%D0%BE%D0%BD
Массовый линкбилдинг для сайта позволяет быстро увеличить ссылочную массу. Программы типа Xrumer автоматизируют размещение ссылок. Это ускоряет рост DR и позиций. Такой метод подходит для разных проектов. Массовый линкбилдинг для сайта – быстрый способ SEO-продвижения.
сервисы продвижения сайтов, раскрутка сайтов луганск, Как настроить Xrumer для рассылок
линкбилдинг что это, услуги для продвижения сайтов, продвижение сео сайта спб
!!Удачи и роста в топах!!
Хай!
Ставим все точки над «i» в вопросе дженериков. [url=https://generik-info.ru/chto-takoe-dzheneriki-prostymi-slovami/]Дженерики это простыми словами[/url]
Переходи: – https://generik-info.ru/chto-takoe-dzheneriki-prostymi-slovami/
Дженерики что это
Дженерики для чего они нужны
Что такое дженерики в медицине
Удачи!
саратов стоимость бетона купить бетон
Доброго!
Долго обмозговывал как поднять сайт и свои проекты и нарастить DR и узнал от гуру в seo,
топовых ребят, именно они разработали недорогой и главное лучший прогон Xrumer – https://www.bing.com/search?q=bullet+%D0%BF%D1%80%D0%BE%D0%B3%D0%BE%D0%BD
Использование Xrumer в 2025 году помогает автоматизировать линкбилдинг. Программа позволяет массово размещать ссылки на форумах. Это экономит время и повышает эффективность SEO. Системный подход увеличивает DR и позиции сайта. Использование Xrumer в 2025 актуально для всех проектов.
авито продвижения сайта, проверить сео страницу, линкбилдинг пример
Как поднять DR сайта за неделю, продвижение сайта интернет магазина москва, разметки seo
!!Удачи и роста в топах!!
Здравствуйте!
Долго не спал и думал как поднять сайт и свои проекты и нарастить TF trust flow и узнал от друзей профессионалов,
отличных ребят, именно они разработали недорогой и главное top прогон Xrumer – https://www.bing.com/search?q=bullet+%D0%BF%D1%80%D0%BE%D0%B3%D0%BE%D0%BD
Линкбилдинг для интернет магазина требует качественных ссылок. Линкбилдинг сайт SEO ускоряет продвижение. Линкбилдинг линкбилдинг на запад открывает новые рынки. Линкбилдинг по тематике повышает релевантность. Что такое линкбилдинг становится понятно при практике.
seo контент сайта, нужен seo, Xrumer форумный спам
Автоматический прогон статей, метрики для сео, seo torrent
!!Удачи и роста в топах!!
[url=https://blackout-shtory.ru/]Рулонные шторы блэкаут с электроприводом идеально подойдут для создания уюта и контроля освещения в вашем доме.[/url]
идеальное решение для. Рулонные шторы блэкаут надежно затемняют помещение, что позволяет создать темную обстановку в любое время суток.
Важным преимуществом рулонных штор блэкаут с электроприводом считается. Управление шторами осуществляется при помощи пульта, что делает их идеальными для современных интерьеров.
Кроме того, рулонные шторы с эффектом блэкаут просто монтируются. Существует несколько способов крепления этих штор. Это позволяет адаптировать шторы под любой тип окон.
Важно отметить, что электроприводные рулонные шторы блэкаут имеют. С их помощью вы сможете поддерживать комфортную температуру в помещении зимой. В итоге, рулонные шторы с блэкаутом и электроприводом станут не только эстетичным, но и функциональным решением.
Добрый день!
Долго думал как поднять сайт и свои проекты и нарастить CF cituation flow и узнал от успещных seo,
крутых ребят, именно они разработали недорогой и главное лучший прогон Xrumer – https://www.bing.com/search?q=bullet+%D0%BF%D1%80%D0%BE%D0%B3%D0%BE%D0%BD
Прогон ссылок для роста позиции улучшает видимость сайта. Xrumer: полное руководство помогает новичкам освоить инструмент. Создание ссылок массовыми методами экономит время. Как настроить Xrumer для рассылок становится понятным после инструкции. Генерация ссылок через Xrumer ускоряет продвижение.
seo за результатами, как сделать сео оптимизацию карточки, Прогон Хрумер для сайта
линкбилдинг план, фриланс раскрутка сайта, продвижение сайта в яндексе самостоятельно
!!Удачи и роста в топах!!
Здравствуйте!
Что скрывается за обещанием «займ под 0%»? [url=https://kredit-bez-slov.ru]Микрофинансовые организации онлайн[/url]
Читай тут: – https://kredit-bez-slov.ru/mikrofinansovye-organizaczii-onlajn/
Дженерики для чего они нужны
Дженерики это простыми словами
Что такое дженерики простыми словами
Бывай!
кашпо для сада купить [url=http://ulichnye-kashpo-kazan.ru/]кашпо для сада купить[/url] .
Всех приветствую! Хотите узнать больше о продвижении? Тут вы можете ознакомиться с ответом на вопрос: http://hipershoes.com/?product=sandalia-cuna-mujer-0953556
Мир прекрасен цитаты. Мудрые высказывания. Короткие цитаты на русском. Цитаты без смысла. Цитаты великих людей про счастье. Короткие цитаты про характер. Цитаты про мысли. Цитаты известных писателей.
How come you do not have your website viewable in mobile format? cant see anything in my Droid.
Всех приветствую! Хотите узнать больше о продвижении? Тут вы можете ознакомиться с ответом на вопрос: https://sayszi.com/youngstonesteak/
принудительное лечение в психиатрическом стационаре
psikhiatr-moskva003.ru
консультация врача психиатра
Здарова!
Практические советы для тех, кто хочет совместить приятное с полезным. [url=https://zarabotok-na-igrah.ru/kak-zarabotat-na-igrah/]играть и заработать деньги[/url]
Читай тут: – https://zarabotok-na-igrah.ru/kak-zarabotat-na-igrah/
заработать биткоин на играх
игры на которых можно заработать
можно ли заработать на играх в телефоне
Пока!
Откройте для себя мир комфорта с [url=https://elektro-shtory.ru/] рулонными шторами с электроприводом[/url], которые идеально подходят для создания уюта в вашем доме.
Рулонные шторы с автоматизированным управлением — это удобное и стильное решение для современных интерьеров. Такие шторы помогают создавать комфортную атмосферу в вашем пространстве и защищают от солнечного света .
Электрические шторы имеют множество преимуществ. Во-первых, управление шторами происходит дистанционно, что особенно удобно в больших помещениях . Кроме того, автоматизация штор дает возможность выбрать режим открытия и закрытия в зависимости от освещения .
Электрические рулонные шторы подойдут для любого типа помещений. Их часто устанавливают в спальнях, гостиных и офисах . Следует помнить, что для работы электропривода необходимо подвести электрический кабель.
Фактор выбора материала и дизайна штор также играет важную роль. Шторы могут быть выполнены из различных тканей, что позволяет выбрать наиболее подходящий вариант для вашего интерьера . Также следует учитывать, что многие компании предоставляют услуги по индивидуальному заказу штор .
Приобретите [url=https://rulonnye-smart-shtory.ru/]все об электроприводах для штор[/url] и насладитесь комфортом и современными технологиями в своем доме.
Рулонные шторы с электроприводом становятся всё более популярными среди современных потребителей. Управление этими шторами можно осуществлять с помощью мобильного приложения или специального пульта.
Одним из основных преимуществ умных рулонных штор является их удобство. С помощью одного нажатия кнопки вы можете регулировать свет и тень в вашем помещении.
Также рулонные шторы могут быть запрограммированы на автоматическое открытие и закрытие. Вы можете задать время, когда шторы должны открываться и закрываться, что делает их особенно удобными.
Эти шторы могут стать частью вашей системы “умный дом”, что добавляет дополнительный уровень комфорта. Таким образом, шторы могут работать в связке с другими устройствами, что делает ваш дом более умным и адаптивным.
I really love this article.
купить горшки для сада [url=http://www.ulichnye-kashpo-kazan.ru]http://www.ulichnye-kashpo-kazan.ru[/url] .
Преобразите ваше пространство с помощью [url=https://pult-shtory.ru/]умных рулонных штор для дома, которые идеально сочетают стиль и современность. [/url]
Дистанционно управляемые рулонные шторы приобретают популярность в современных интерьерах. Данные изделия соединяют в себе удобство и эстетичность, что делает их идеальным выбором для различных помещений.
Вы можете контролировать рулонные шторы либо с помощью пульта, либо через мобильное приложение. Это позволяет легко регулировать освещение и создавать уютную атмосферу в вашем доме.
Помимо этого, рулонные шторы представлены в множестве дизайнов и цветовых вариантах. Таким образом, вы сможете выбрать именно тот вариант, который идеально впишется в ваш интерьер.
Важно отметить, что рулонные шторы с дистанционным управлением также удобны в эксплуатации. Их просто поддерживать в чистоте, и они не требуют сложного ухода, что идеально подходит для занятых людей.
[url=https://fr.bonuscodes.com/code-promo-1xbet-burkina-faso]альфацетилметадол[/url]
Закажите бета-метадол прямо сейчас и получите скидку.
Здравствуйте!
Хватит винить себя в увольнении. [url=https://zhit-legche.ru/kak-perezhit-uvolnenie/]как пережить увольнение с работы форум[/url]
Здесь подробней: – https://zhit-legche.ru/kak-perezhit-uvolnenie/
хочу уволиться но не могу решиться
увольнение с работы
как пережить увольнение с работы
До встречи!
Преобразите ваше пространство с помощью [url=https://pult-shtory.ru/]умных рулонных штор для дома, которые идеально сочетают стиль и современность. [/url]
Дистанционно управляемые рулонные шторы приобретают популярность в современных интерьерах. Эти шторы предлагают удобство и стиль, что делает их отличным решением для любого помещения.
Вы можете контролировать рулонные шторы либо с помощью пульта, либо через мобильное приложение. Благодаря этому вы сможете легко настраивать уровень света и атмосферу в вашем доме.
Также рулонные шторы доступны в различных стилях и цветовых решениях. Это позволит вам подобрать идеальный вариант, который будет гармонировать с вашим интерьером.
Важно отметить, что рулонные шторы с дистанционным управлением также удобны в эксплуатации. Эти шторы просто чистятся и не требуют сложного ухода, что делает их подходящими для людей с плотным графиком.
[url=https://akkum-shtory.ru/]Рулонные шторы с аккумулятором[/url] предоставляют удобство и стиль для любого интерьера, позволяя легко управлять светом и обеспечивая полную свободу от проводов.
Одним из основных преимуществ таких штор является их удобство.
консультация врача психиатра онлайн
psychiatr-moskva001.ru
консультация психиатра на дому
реабилитация от алкогольной зависимости
reabilitaciya-astana001.ru
реабилитация зависимых от алкоголя в Астане
лечение и реабилитация алкоголизма
reabilitaciya-astana002.ru
реабилитационный центр для алкоголиков в Астане
youtube 8409
где лечиться от алкоголизма
reabilitaciya-astana003.ru
как вылечить алкогольную зависимость
Добрый день!
Честный гайд по миру казино для тех, кто хочет понять правила, а не просто слить деньги. [url=http://nagny-casino.ru/kazino-s-bystrym-vyvodom/]казино без депозита[/url]
Читай тут: – http://nagny-casino.ru/kazino-s-bystrym-vyvodom/
игры на деньги без паспорта
10 лучших казино онлайн
казино на деньги
Пока!
888starz бонус как использовать
кашпо для цветов напольное [url=http://kashpo-napolnoe-moskva.ru/]кашпо для цветов напольное[/url] .
Здравствуйте!
[url=https://pro-telefony.ru/chto-delat-esli-kupil-seryj-telefon/]Что значит серый телефон?[/url] Новая реальность: как теперь безопасно покупать смартфоны в России?
Читай тут: – https://pro-telefony.ru/chto-delat-esli-kupil-seryj-telefon/
Что значит серый телефон
Серый телефон как проверить
Как зарегистрировать серый телефон
Пока!
Добрый день!
Надоело жаловаться друзьям на работу, но ничего не менять? [url=https://zhit-legche.ru/hochu-uvolitsya-no-ne-mogu-reshitsya/]как пережить увольнение[/url]
Переходи: – https://zhit-legche.ru/hochu-uvolitsya-no-ne-mogu-reshitsya/
как пережить увольнение с любимой работы
хочу уволится с работы
хочу уволиться но не могу решиться
Будь здоров!
вывод из запоя краснодар
narkolog-krasnodar011.ru
вывод из запоя круглосуточно краснодар
Конфиденциальная наркологическая помощь в Красноярске – это эффективный способ справиться с зависимостями. Наркологическая клиника Красноярск предоставляет качественное лечение зависимостивключая конфиденциальное лечение алкоголизма и программу лечения наркотической зависимости. Мы обеспечиваем квалифицированные консультации нарколога и медицинскую помощь при алкоголизме, а также детоксикацию организма. Реабилитация наркоманов включает психотерапию при зависимостях и группы поддержки для зависимых. Необходимо отметить, что поддержка близких зависимых является важным фактором в восстановлении после зависимости. Обратитесь за помощью на vivod-iz-zapoya-krasnoyarsk010.ru для получения информации о наших услугах.
вывод из запоя
narkolog-krasnodar012.ru
вывод из запоя цена
Зависимость от алкоголя — это серьезная проблема, которая касается не только зависимого, но и окружающих его людей. Вызов нарколога на дом в Красноярске является начальным этапом к лечению алкогольной зависимости. Обсуждение с наркологом поможет оценить степень проблемы и рекомендовать подходы к лечению, включая психотерапию при алкоголизме.Проблемы в семье из-за алкоголя часто приводят к кризису в семье. Помощь со стороны семьи играет ключевую роль в возстановлении здоровья. Семье необходимо знать, как поддержать, и какие советы по борьбе с зависимостью могут быть полезны. Лечение алкоголиков включает в себя медицинские методы, но и поддержку социума. Предотвращение алкоголизма начинается с осознания проблемы и готовности к изменениям. Восстановление отношений — это долгий процесс, который требует усилий всей семьи. вызов нарколога на дом Красноярск Вызов врача на дом дает возможность получить помощь в комфортной обстановке, что способствует лучшему восприятию информации и уменьшает стресс. Помощь семье и согласие на лечение — это основные этапы на дороге к восстановлению.
вывод из запоя круглосуточно
narkolog-krasnodar012.ru
вывод из запоя цена
вывод из запоя цена
narkolog-krasnodar013.ru
вывод из запоя круглосуточно краснодар
Центр реабилитации алкоголиков в Красноярске предоставляет возможность начать жизнь с чистого листа для людей, страдающих от зависимости. Вызвать нарколога на дом можно для первоначальной оценки состояния и проверки здоровья. Лечение алкоголизма включает комплексный подход с медицинским контролем и психотерапевтической поддержкой, что обеспечивает персонализированный подход к каждому человеку. Реабилитационная программа включает процесс восстановления после алкогольной зависимости и социальную адаптацию, а также помощь близким. Группы анонимных алкоголиков помогают наладить связь с единомышленниками. Наркологическая помощь в нашем центре позволяет справиться с зависимостью и начать новую жизнь.
youtube 8612
экстренный вывод из запоя
narkolog-krasnodar013.ru
вывод из запоя
Здарова!
Узнай, как работают их дешевые аналоги — дженерики. [url=https://generik-info.ru/analogi-lekarstv-deshevle/]Дженерики что это[/url]
Читай тут: – https://generik-info.ru/analogi-lekarstv-deshevle/
Дженерики это простыми словами
Что такое дженерики лекарства
Дженерики что это
Удачи!
экстренный вывод из запоя
narkolog-krasnodar014.ru
вывод из запоя круглосуточно краснодар
экстренный вывод из запоя смоленск
vivod-iz-zapoya-smolensk013.ru
экстренный вывод из запоя смоленск
Цены на ремонт https://remontkomand.kz/ru/price квартир и помещений в Алматы под ключ. Узнайте точные расценки на все виды работ — от демонтажа до чистовой отделки. Посчитайте стоимость своего ремонта заранее и убедитесь в нашей прозрачности. Никаких «сюрпризов» в итоговой смете!
экстренный вывод из запоя
narkolog-krasnodar014.ru
вывод из запоя круглосуточно краснодар
вывод из запоя
narkolog-krasnodar015.ru
вывод из запоя круглосуточно краснодар
youtube 7862
купить напольное кашпо для комнатных растений [url=http://kashpo-napolnoe-moskva.ru/]http://kashpo-napolnoe-moskva.ru/[/url] .
вывод из запоя круглосуточно
narkolog-krasnodar015.ru
лечение запоя краснодар
лечение запоя
vivod-iz-zapoya-smolensk015.ru
вывод из запоя
Прокапка после алкогольной зависимости — это ключевая медицинская манипуляция, направленная на детоксикацию организма и восстановление состояния здоровья пациента . Во время вызова нарколога на дом срочно проводится внутривенное введение препаратов для капельницы , что способствует очищению крови от токсичных веществ, накопленных в результате алкогольной зависимости . Нарколог на дом срочно Процедура обычно включает в себя введение солевых растворов, витаминов и минералов , что способствует улучшению самочувствия и уменьшает проявления похмелья. Уход на дому позволяет пациенту находиться в привычной обстановке , что играет важную роль в процессе реабилитации. Наркологическая помощь включает поддержку пациента , что значительно повышает шансы на восстановление организма после алкоголя . Важно следовать советам по лечению и регулярно проходить процедуру прокапки для достижения оптимальных результатов.
Прокапаться от алкоголя анонимно – существенный этап на дороге к выздоровлению. На сайте narkolog-tula015.ru вы можете ознакомиться с информацией о методах борьбы с алкоголизмом и программах реабилитации. Анонимные группытакие как группа Анонимных Алкоголиков, предлагают поддержку зависимым и их близким. Психотерапевтические методы помогает справиться с кризисом из-за алкоголя. Методы кодирования от алкоголя и советы по отказу от спиртного также могут быть полезными борьбы с зависимостью. Программы трезвости помогают сохранить здоровье и построить жизнь без алкоголя. Поддержка людям с алкоголизмом доступна всем, кто нуждается в ней.
В нашем современном мире проблема зависимости высвечивается все ярче. Если вы или ваши близкие столкнулись с зависимостью, не бойтесь обратиться за помощью. Анонимный вызов врача нарколога в Красноярске является значимым этапом на пути к избавлению от зависимости. На сайте site;com доступна возможность записи на консультацию к наркологу, который предоставит медицинскую помощь и обеспечит полную анонимность пациента.Профессиональная помощь при алкоголизме и наркомании неизменно требуют компетентного подхода. В центр по лечению зависимостей доступны услуги, такие как психотерапия и психологическая поддержка. Вызов врача на дом обеспечит комфортные условия для пациента, что особенно важно в сложных ситуациях. Не затягивайте с помощью, обратитесь за анонимной помощью уже сегодня!
Лечение запоя в Туле: советы для родственников и близких Запой в Туле: что делать? часто требует вмешательства специалистов. Капельница — это эффективный способ облегчить симптомы запоя, такие как обезвоживание, интоксикация и физические недомогания. Важно помнить, что помощь родственников играет ключевую роль в процессе восстановления. лечение запоя тула При наличии алкогольной зависимости, поддержка семьи может значительно ускорить лечение. Симптомы запоя, такие как раздражительность, потливость и дрожь, требуют немедленной медицинской помощи. Наркология на дому предлагает услуги по введению капельниц на дому, что делает процесс менее стрессовым для пациента. Советы близким: будьте терпеливыми и не осуждайте. Уход за больным включает заботу о его психологическом состоянии, так как психология зависимости влияет на успешность лечения. Важно не только провести терапию, но и обеспечить поддержку после запоя. Реабилитация наркозависимых требует комплексного подхода, включая психологическую помощь и дальнейшее наблюдение. Помимо капельницы, стоит рассмотреть возможные шаги по лечению алкоголизма, которое включает встречи с психотерапевтом и участие в реабилитационных программах. Домашняя терапия также может быть полезной, однако она должна проводиться под наблюдением медика.
Наркологические услуги на дому в Красноярске становятся всё актуальней. Специалисты данной сферы, предлагают широкий спектр наркологических услуг, в т.ч. помощь при алкоголизме и других зависимостях. Консультация нарколога на дому позволяет быстро провести диагностику зависимостей и назначить индивидуальный подход к пациенту. Анонимное лечение – ключевая особенность работы наркологов, что особенно важно для людей, которые стесняются обращаться в медицинские учреждения. Реабилитация на дому предполагает психотерапевтическую поддержку, восстановительные программы и медикаментозное лечение. Поддержка семей зависимых является важным фактором на пути к выздоровлению. Предотвращение рецидивов также является важной частью работы наркологов. Специалисты предлагают психологическую помощь и поддержку, помогая пациентам справляться с трудностями на пути к выздоровлению. Узнать больше о предлагаемых услугах можно на сайте vivod-iz-zapoya-krasnoyarsk011.ru, где вы найдёте всю необходимую информацию и контакты по наркологическим услугам в Красноярске.
Эффективные методы лечения алкоголизма в Туле Алкоголизм – это огромная проблема‚ необходима комплексная стратегия. В Туле доступны многочисленные наркологические услуги‚ включая опцию вызова нарколога на дом. Это особенно существенно для людей‚ кто не хочет посещать клиники для лечения алкоголизма. Первым этапом является детоксикация тела‚ которая помогает избавиться от алкоголя и его токсинов. После этого начинается терапия алкогольной зависимости. Программы лечения алкоголизма могут включать как медикаментозное лечение, так и психологическую поддержку при лечении. Консультация нарколога поможет выбрать наиболее эффективный путь. Реабилитация зависимых предполагает наличие семейной терапиичто способствует поддержке близких. Важно помнить о профилактике рецидивов‚ который включает занятия в группах поддержки и индивидуальные сессии. Анонимное лечение алкоголизма позволяет пациентам быть уверенными в своей конфиденциальности. Важно помнить‚ что процесс лечения алкогольной зависимости длительный‚ что требует терпения и усилий. Вызвать нарколога на дом – это начало новой жизни без алкоголя.
Добрый день!
Деньги на карту за 5 минут – звучит круто, правда? [url=https://kredit-bez-slov.ru/kak-bystro-sdelat-kreditnuyu-istoriyu/]Получить кредит с плохой историей быстро[/url]
По ссылке: – https://kredit-bez-slov.ru/kak-bystro-sdelat-kreditnuyu-istoriyu/
Дженерики что это такое
Что такое дженерики простыми словами
Дженерики для чего они нужны
Покеда!
Вызов врача нарколога в Красноярске — это необходимый шаг для людей, нуждающихся в помощи при зависимости. На сайте vivod-iz-zapoya-krasnoyarsk012.ru можно получить сведения о помощи наркологов, включая выявление зависимостей и лечение медикаментами. Наши специалисты предлагают консультацию нарколога и лечение без разглашения. Служба выездной наркологии готова оказать неотложную помощь при запое или других ситуациях. Наши услуги включают стационарное лечение и реабилитацию наркоманов для пациентов с наркотической зависимостью. Мы оказываем помощь зависимым и их близким и проводим профилактику зависимостей. Не откладывайте помощь — вызовите нарколога и начните путь к выздоровлению.
Капельница для вывода из запоя — действующий способ устранить признаки алкогольной зависимости. В Туле множество клиникспециализирующихся на лечении зависимостей предлагают помощь по выводу из запоя, но необходимо выбрать подходящую.Начальным этапом является диагностика зависимости. Квалифицированные специалисты осуществят оценку состояния пациента и разработают персонализированный план лечения. Необходимочтобы клиника предоставляла стационарное лечение и конфиденциальность при лечении алкогольной зависимости. Это обеспечит комфортные условия для пациентов.Обратите внимание на наличии психотерапии при алкоголизме. Психотерапия играет ключевую роль в реабилитации после запоя и лечении алкоголизма. Семейная поддержка также способствует успешной реабилитации зависимых. вывод из запоя тула Изучите отзывы о медицинских учреждениях и проверьте, какие услуги предоставляет нарколог. Правильный выбор клиники — это залог успешного и безопасного выздоровления.
Лечение похмелья с помощью капельницы — это эффективное средство для ликвидации неприятных ощущений интоксикации после изобилия спиртного. При похмелье организм испытывает дискомфорт от недостатка жидкости и нехватки электролитов, что способствует головной боли. Процедура с капельницей включает в себя вливание специальных растворов и восстановление баланса веществ. Консультация специалиста может включать в себя специальные препараты от похмелья, которые помогают организму избавиться от токсинов. Капельницы часто содержат минералы, вещества для детоксикации, которые ускоряют процесс выздоровления. Поддержка организма таким образом позволяет значительно уменьшить симптомы похмелья и помочь восстановиться. Для получения капельницы можно обратиться в клинику или заказать выезд врача через сайт narkolog-tula019.ru. Не забывайте, что оперативное вмешательство поможет предотвратить осложнения.
вывод из запоя
vivod-iz-zapoya-smolensk013.ru
лечение запоя смоленск
ДОСТУПНЫЙ ВЫВОД ИЗ ЗАПОЯ В ТУЛЕ: РЕАЛЬНОСТЬ И МИФЫ Лечение алкоголизма – это сложный и многогранный процесс, требующий комплексного подхода. В городе Тула существует множество наркологических клиник, предлагающих лечение запоя и реабилитацию от запоя, однако есть мифы о лечении алкоголизма, способные ввести в заблуждение. Во-первых, широко распространено мнение, что вывод из запоя происходит быстро. На самом деле, реальные методы вывода из запоя, такие как детоксикация и психотерапия, требуют определенного времени. Наркологическая клиника Тула в Туле предлагает программы реабилитации, в рамках которых специалисты оказывают помощь в восстановлении после запоя. Важно отметить, что психотерапия имеет центральное значение в процессе лечения зависимости. Консультация нарколога поможет выявить причины зависимости и разработать индивидуальную программу лечения. Не стоит забывать, что лечение зависимости в Туле доступно и эффективно, если обратиться за помощью вовремя.
ПРОКАПАТЬСЯ ОТ ЗАПОЯ: КОГДА ЭТО НЕОБХОДИМО Запой – это серьезная проблема, для решения которой нужна медицинская помощь. В Туле и других городах лечение запоя включает детоксикацию от алкоголя, что является ключевым этапом в процессе восстановления. Симптомы запойного алкоголизма могут проявляться в виде тревожности‚ бессонницы и физической зависимости. Лечение запойного состояния должно быть комплексным. Стационарное лечение зависимости с реабилитационными программами гарантирует безопасность пациента и предоставляет психологическую поддержку в борьбе с зависимостью. Консультация нарколога поможет подобрать индивидуальное лечение алкогольной зависимости‚ что включает в себя как медикаменты‚ так и психотерапию. лечение запоя тула Родственники алкозависимого человека играют важную роль в предотвращении рецидивов алкоголизма. Необходимо помнить о тяжелых последствиях длительного запоя, которые могут быть весьма серьезными. Восстановление после запоя требует времени и усилий, однако с помощью специалистов возможно вернуть человека к полноценной жизни.
youtube 5963
вывод из запоя круглосуточно
vivod-iz-zapoya-smolensk014.ru
вывод из запоя круглосуточно
youtube 5835
Капельницы от запоя на дому — является эффективным способом очищения организма при борьбе с алкоголизмом. Нарколог на дом анонимно в Туле предлагает услуги по проведению капельниц, что позволяет быстро восстановить здоровье пациентов . Состав капельного раствора включает в себя медикаментов , которые способствуют устранению симптомов запойного алкоголизма , таких как обезвоживание и интоксикация . Нарколог на дом анонимно Тула. Основные компоненты капельницы : раствор натрия хлорида для гидратации , глюкоза для энергии, витамины группы B для нормализации обмена веществ и специальные медикаменты для снятия абстинентного синдрома ; лекарства для капельницы подбираются индивидуально , учитывая состояние пациента . Лечение на дому под наблюдением нарколога обеспечивает анонимное лечение , что существенно для многих зависимых от алкоголя. Поддержка семьи при запое имеет решающее значение для успешного выздоровления. Консультация нарколога поможет определить дальнейшие шаги , включая реабилитацию алкоголиков и восстановление после алкогольной зависимости.
Услуги по откачке в Туле, важная услуга для поддержания гигиеничности в вашем доме. Проблемы с канализацией могут возникнуть неожиданно, и в таких случаях необходимо вызвать профессионалов. Качественная откачка сточных вод поможет избежать неприятных ситуаций.Среди вариантов откачки предлагаются: очистка канализации, обслуживание выгребных ям и экстренная откачка. Ассенизаторская машина обеспечит качественное выполнение работ в соответствии с экологическими нормами. На сайте narkolog-tula019.ru вы можете узнать информацию о ценах на услуги и вариантах вызова специалиста. Также доступны сушилки септиков и системы дренажа для минимизации повторных засоров. Не откладывайте на потом — решите проблемы с канализацией сегодня!
youtube 7538
лечение запоя
vivod-iz-zapoya-smolensk015.ru
лечение запоя смоленск
пансионат с медицинским уходом
pansionat-msk007.ru
пансионат инсульт реабилитация
Выезд нарколога – это удобный способ достать квалифицированную медицинскую помощь в лечении зависимости. Многие пациенты боятся и стесняются, обращаясь в стационары, поэтому конфиденциальное лечение становится необходимостью. Специалисты, работающие на сайте narkolog-tula020.ru, предлагают услуги по очищению организма и психологической помощи, что позволяет успешно справляться с алкогольной зависимостью и наркоманией. Консультация нарколога включает в себя диагностику состояния пациента и создание персонального плана лечения. Важно осознавать, что забота о пациенте со стороны близких также является важным элементом в реабилитации. Работа с семьей и помощь в кризисной ситуации помогут формировать окружение поддержки для пациента, что существенно повышает вероятность на выздоровление.
Здравствуйте!
Пора зарабатывать на этом, и я расскажу, как это сделать. [url=https://zarabotok-na-igrah.ru/na-kakih-igrah-mozhno-zarabotat-realnye-dengi/]игры на которых можно заработать деньги[/url]
Читай тут: – https://zarabotok-na-igrah.ru/na-kakih-igrah-mozhno-zarabotat-realnye-dengi/
заработать деньги на играх без вложений
заработок на игровой валюте
на каких играх можно заработать реальные деньги
Покеда!
пансионат с медицинским уходом
pansionat-msk008.ru
пансионат для пожилых людей
Вызов врача нарколога — необходимая мера для тех‚ кто столкнулся с зависимостями. Услуги нарколога включает диагностику зависимости и лечение‚ что особенно актуально в кризисных ситуациях. Обратившись на narkolog-tula021.ru‚ вы можете получить анонимный вызов врача на дом. Это удобно и безопасно. Услуги нарколога на дому обеспечивают удобные условия для клиентов. Прием у нарколога позволяет выявить степень зависимости и назначить индивидуальную программу лечения. В реабилитации пациентов важна поддержка для родственников‚ что способствует эмоциональной стабильности. Наркологическая клиника предлагает всеобъемлющее лечение‚ включая психотерапевтические сеансы и медикаментозное лечение зависимостей. Не стоит откладывать обращение за помощью‚ ведь своевременное лечение алкоголизма и наркотической зависимости может спасти жизнь.
пансионат для лежачих москва
pansionat-msk009.ru
пансионат для лежачих москва
частные пансионаты для пожилых в москве
pansionat-msk007.ru
пансионат для людей с деменцией в москве
частный пансионат для престарелых
pansionat-tula007.ru
пансионат после инсульта
дешевый интернет екатеринбург
inernetvkvartiru-ekaterinburg004.ru
проверить интернет по адресу
напольные горшки для цветов купить интернет магазин [url=www.kashpo-napolnoe-krasnodar.ru]напольные горшки для цветов купить интернет магазин[/url] .
частные пансионаты для пожилых в москве
pansionat-msk008.ru
пансионат с медицинским уходом
частный пансионат для пожилых
pansionat-tula008.ru
пансионаты для инвалидов в туле
провайдеры интернета по адресу
inernetvkvartiru-ekaterinburg005.ru
интернет тарифы екатеринбург
Нужен клининг? рейтинг клининговых компаний москвы 2026. Лучшие сервисы уборки квартир, домов и офисов. Сравнение услуг, цен и отзывов, чтобы выбрать надежного подрядчика.
youtube 9814
пансионат для пожилых в москве
pansionat-msk009.ru
пансионат для пожилых
пансионат для престарелых
pansionat-tula009.ru
частный пансионат для престарелых
домашний интернет в екатеринбурге
inernetvkvartiru-ekaterinburg006.ru
интернет тарифы екатеринбург
Хай!
Почему казино любит, когда вы выигрываете? [url=https://nagny-casino.ru/onlajn-kazino-bez-liczenzii/]олимп казино[/url]
По ссылке: – https://nagny-casino.ru/onlajn-kazino-bez-liczenzii/
номад казино
рейтинг казино
777 казино
Будь здоров!
youtube 3183
консультация врача психиатра онлайн
psychiatr-moskva004.ru
психиатр на дом
пансионат с деменцией для пожилых в туле
pansionat-tula007.ru
пансионат для лежачих пожилых
youtube 7499
подключение интернета по адресу
inernetvkvartiru-krasnoyarsk004.ru
интернет провайдеры по адресу
youtube 6501
youtube 9097
9003
7392
госпитализация в психиатрический стационар
psychiatr-moskva005.ru
вызов психиатра на дом в москве
пансионат для пожилых людей
pansionat-tula008.ru
пансионат для пожилых людей
2159
5898
провайдеры по адресу красноярск
inernetvkvartiru-krasnoyarsk005.ru
провайдеры по адресу
платная консультация психиатра
psychiatr-moskva006.ru
вызов психиатрической скорой помощи
пансионат для лежачих тула
pansionat-tula009.ru
пансионат для престарелых людей
интернет провайдеры по адресу
inernetvkvartiru-krasnoyarsk006.ru
интернет провайдеры по адресу дома
психиатрическая клиника стационар
psikhiatr-moskva004.ru
нужна консультация психиатра
Приветствую!
Безопасность прежде всего, особенно при анонимных сделках. [url=https://pro-kriptu.ru/gde-kupit-kriptovalyutu-bez-verifikaczii/]крипта без kyc[/url]
По ссылке: – https://pro-kriptu.ru/gde-kupit-kriptovalyutu-bez-verifikaczii/
куда вложить крипту без верификации
defi проекты с доходом
перспективные альткоины
До встречи!
частная психиатрическая помощь
psychiatr-moskva004.ru
круглосуточная психиатрическая помощь
интернет провайдеры в краснодаре по адресу дома
inernetvkvartiru-krasnodar004.ru
провайдеры по адресу
фабрика пошива одежды [url=nitkapro.ru]nitkapro.ru[/url] .
комплексное продвижение сайтов москва [url=kompanii-zanimayushchiesya-prodvizheniem-sajtov.ru]kompanii-zanimayushchiesya-prodvizheniem-sajtov.ru[/url] .
интернет агентство продвижение сайтов сео [url=https://poiskovoe-prodvizhenie-sajta-v-internete-moskva.ru]https://poiskovoe-prodvizhenie-sajta-v-internete-moskva.ru[/url] .
аудит продвижения сайта [url=www.poiskovoe-seo-v-moskve.ru]www.poiskovoe-seo-v-moskve.ru[/url] .
продвижение в google [url=http://internet-agentstvo-prodvizhenie-sajtov-seo.ru/]http://internet-agentstvo-prodvizhenie-sajtov-seo.ru/[/url] .
напольный горшок для цветов [url=https://kashpo-napolnoe-krasnodar.ru]напольный горшок для цветов[/url] .
seo partners [url=www.poiskovoe-prodvizhenie-moskva-professionalnoe.ru/]seo partners[/url] .
seo продвижение и раскрутка сайта [url=www.internet-prodvizhenie-moskva.ru]seo продвижение и раскрутка сайта[/url] .
There is a lot of misunderstanding about these issues today. Your material helps explain things.
госпитализация в психиатрический стационар
psikhiatr-moskva005.ru
вызов психиатрической помощи
консультация психиатра по телефону
psychiatr-moskva005.ru
платная психиатрическая клиника
провайдеры по адресу дома
inernetvkvartiru-krasnodar005.ru
подключение интернета по адресу
частная психиатрическая клиника стационар
psikhiatr-moskva006.ru
психиатр на дом для пожилого
психиатрическая медицинская помощь
psychiatr-moskva006.ru
психиатрическая клиника
подключить интернет по адресу
inernetvkvartiru-krasnodar006.ru
провайдеры интернета в краснодаре по адресу проверить
Добрый день!
Надоело проходить верификацию на каждой бирже? [url=https://pro-kriptu.ru/birzhi-kriptovalyut-bez-verifikaczii/]где купить крипту без верификации[/url]
Читай тут: – https://pro-kriptu.ru/birzhi-kriptovalyut-bez-verifikaczii/
defi проекты с доходом
крипта без kyc
где можно купить криптовалюту без верификации
Будь здоров!
реабилитация наркоманов
reabilitaciya-astana004.ru
лечение наркомании
seo network [url=internet-agentstvo-prodvizhenie-sajtov-seo.ru]seo network[/url] .
интернет провайдеры москва
inernetvkvartiru-msk004.ru
домашний интернет
оказание психиатрической помощи
psikhiatr-moskva004.ru
врач психиатр на дом в москве
анонимная реабилитация наркозависимых в Астане
reabilitaciya-astana005.ru
анонимное лечение от наркозависимости
узнать интернет по адресу
inernetvkvartiru-msk005.ru
провайдер интернета по адресу москва
вызов психиатрической скорой помощи
psikhiatr-moskva005.ru
круглосуточная психиатрическая помощь
There is a lot of misunderstanding about these issues today. Your material helps explain things.
эффективное лечение алкоголизма
reabilitaciya-astana006.ru
как избавить человека от алкогольной зависимости
производство по пошиву одежды [url=https://nitkapro.ru/]https://nitkapro.ru/[/url] .
swot анализ варианты https://swot-analiz1.ru
подключить интернет по адресу
inernetvkvartiru-msk006.ru
провайдеры интернета в москве по адресу проверить
Здарова!
Азартные штуки и как с ними жить. [url=https://nagny-casino.ru/igry-na-dengi/]слоты играть без верификации[/url]
Читай тут: – https://nagny-casino.ru/igry-na-dengi/
топ нелегальных казино
онлайн казино без лицензии
казино онлайн
До встречи!
частная психиатрическая помощь
psikhiatr-moskva006.ru
принудительное лечение в психиатрической больнице
cjc 1295 ipamorelin vs igf-1 lr3 reddit
References:
https://www.jr-it-services.de:3000/bertiemccary9
продвижение по трафику [url=http://internet-agentstvo-prodvizhenie-sajtov-seo.ru/]продвижение по трафику[/url] .
технического аудита сайта [url=http://www.internet-prodvizhenie-moskva.ru]технического аудита сайта[/url] .
вывод из запоя тула
tula-narkolog004.ru
вывод из запоя
seo partner [url=www.poiskovoe-prodvizhenie-sajta-v-internete-moskva.ru/]www.poiskovoe-prodvizhenie-sajta-v-internete-moskva.ru/[/url] .
Здравствуйте!
Стримы, продажа аккаунтов, NFT и киберспорт. [url=https://zarabotok-na-igrah.ru/na-kakih-igrah-mozhno-zarabotat-bez-vlozhenij/]заработать деньги на играх[/url]
Написал: – https://zarabotok-na-igrah.ru/na-kakih-igrah-mozhno-zarabotat-bez-vlozhenij/
игры на которых можно заработать
на каких играх можно заработать деньги
заработать денег на играх
Бывай!
профессиональное продвижение сайтов [url=https://kompanii-zanimayushchiesya-prodvizheniem-sajtov.ru/]профессиональное продвижение сайтов[/url] .
раскрутка сайта москва [url=poiskovoe-prodvizhenie-moskva-professionalnoe.ru]раскрутка сайта москва[/url] .
дешевый интернет нижний новгород
inernetvkvartiru-nizhnij-novgorod004.ru
провайдеры по адресу нижний новгород
центр реабилитация алкоголиков
reabilitaciya-astana004.ru
реабилитация наркозависимых наркология
защитная транспортировочная пленка [url=www.samokleyushchayasya-plenka-1.ru]www.samokleyushchayasya-plenka-1.ru[/url] .
элитная дизайнерская мебель цена [url=https://www.dizajnerskaya-mebel-1.ru]https://www.dizajnerskaya-mebel-1.ru[/url] .
вывод из запоя тула
tula-narkolog005.ru
лечение запоя
лучший интернет провайдер нижний новгород
inernetvkvartiru-nizhnij-novgorod005.ru
подключить проводной интернет нижний новгород
реабилитация наркозависимых наркология
reabilitaciya-astana005.ru
анонимное лечение наркомании
вывод из запоя цена
tula-narkolog006.ru
вывод из запоя цена
интернет провайдер нижний новгород
inernetvkvartiru-nizhnij-novgorod006.ru
домашний интернет подключить нижний новгород
лечение и реабилитация алкоголизма
reabilitaciya-astana006.ru
курс лечения от алкоголизма
лечение запоя
vivod-iz-zapoya-chelyabinsk007.ru
вывод из запоя челябинск
продвижение сайта [url=https://www.internet-agentstvo-prodvizhenie-sajtov-seo.ru]продвижение сайта[/url] .
интернет агентство продвижение сайтов сео [url=https://poiskovoe-seo-v-moskve.ru/]poiskovoe-seo-v-moskve.ru[/url] .
Пользуйтесь уникальным предложением и вводите код [url=https://moldovanews.md/wp-content/pages/kak_sdelaty_domashnyuyu_kuragu_iz_abrikosov_sekrety_i_sovety.html]https://moldovanews.md/wp-content/pages/kak_sdelaty_domashnyuyu_kuragu_iz_abrikosov_sekrety_i_sovety.html[/url] для получения бонусов на 1xbet!
1xbetbestcode — это лучший способ сделать свою ставку более выгодной .
Привет!
Импорт техники через таможню: практическое руководство. [url=https://pro-telefony.ru/elektronika-iz-kitaya-napryamuyu/]телефоны оптом из китая[/url]
Написал: – https://pro-telefony.ru/elektronika-iz-kitaya-napryamuyu/
электроника с aliexpress
телефон с алиэкспресс
телефон китайский
Покеда!
интернет провайдеры в новосибирске по адресу дома
inernetvkvartiru-novosibirsk004.ru
интернет провайдеры новосибирск
Привет!
Индийская фарма для личного использования — как получить. [url=https://generik-info.ru/gde-zakazat-tabletki-napryamuyu-iz-indii/]где заказать таблетки напрямую из Индии[/url] Полная инструкция по законному импорту препаратов.
Переходи: – https://generik-info.ru/gde-zakazat-tabletki-napryamuyu-iz-indii/
таблетки от давления производство индия
индийские таблетки
таблетки от давления индия
Пока!
Как сам!
Как делать деньги в криптовалютах не торгуя. [url=https://pro-kriptu.ru/defi-proekty-s-dohodom/]как заработать на инвестициях defi[/url] DeFi протоколы для долгосрочного пассивного дохода.
Читай тут: – https://pro-kriptu.ru/defi-proekty-s-dohodom/
defi кредитование
defi как заработать
что такое defi и как на этом заработать
Покеда!
экстренный вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk008.ru
вывод из запоя круглосуточно челябинск
вывод из запоя цена
tula-narkolog004.ru
лечение запоя
провайдер интернета по адресу новосибирск
inernetvkvartiru-novosibirsk005.ru
провайдер интернета по адресу новосибирск
экстренный вывод из запоя
vivod-iz-zapoya-chelyabinsk009.ru
экстренный вывод из запоя челябинск
лечение запоя
tula-narkolog005.ru
вывод из запоя тула
подключить интернет по адресу
inernetvkvartiru-novosibirsk006.ru
домашний интернет тарифы
вывод из запоя круглосуточно череповец
vivod-iz-zapoya-cherepovec010.ru
лечение запоя
вывод из запоя
tula-narkolog006.ru
вывод из запоя круглосуточно
статьи про продвижение сайтов [url=http://blog-o-marketinge.ru]статьи про продвижение сайтов[/url] .
интернет маркетинг статьи [url=http://blog-o-marketinge1.ru/]интернет маркетинг статьи[/url] .
маркетинговый блог [url=statyi-o-marketinge2.ru]statyi-o-marketinge2.ru[/url] .
строительство домов [url=www.stroitelstvo-domov-irkutsk-2.ru]www.stroitelstvo-domov-irkutsk-2.ru[/url] .
помощь нарколога [url=https://narkologicheskaya-klinika-12.ru/]narkologicheskaya-klinika-12.ru[/url] .
платный наркологический диспансер москва [url=https://narkologicheskaya-klinika-11.ru/]https://narkologicheskaya-klinika-11.ru/[/url] .
вывод из запоя круглосуточно череповец
vivod-iz-zapoya-cherepovec011.ru
вывод из запоя цена
подключить домашний интернет ростов
inernetvkvartiru-rostov004.ru
интернет домашний ростов
вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk007.ru
лечение запоя челябинск
Porque con el gozo de entrambos,crescer les ya la franqueza en el dar,ラブドール 通販
вывод из запоя
vivod-iz-zapoya-cherepovec012.ru
лечение запоя
подключить интернет ростов
inernetvkvartiru-rostov005.ru
домашний интернет тарифы
вывод из запоя челябинск
vivod-iz-zapoya-chelyabinsk008.ru
вывод из запоя цена
9376
вывод из запоя круглосуточно
vivod-iz-zapoya-irkutsk007.ru
лечение запоя иркутск
Привет!
Покер для умных пацанов: играем с расчетом а не на авось. [url=https://nagny-casino.ru/kak-vyigrat-v-poker/]как выиграть в покер[/url] Все инструменты для превращения хобби в источник прибыли.
По ссылке: – https://nagny-casino.ru/kak-vyigrat-v-poker/
как выиграть в покер
покер как играть
как играть в покер онлайн
Пока!
Хай!
Выбираем телефон для стариков: все варианты на столе. [url=https://pro-telefony.ru/telefon-dlya-pozhilyh-lyudej/]моб телефон для пожилых людей[/url] От простых кнопочных до навороченных смартфонов.
Здесь подробней: – https://pro-telefony.ru/telefon-dlya-pozhilyh-lyudej/
кнопочный телефон для пожилых с громким динамиком
лучший кнопочный телефон для пожилых
До встречи!
подключить интернет тарифы ростов
inernetvkvartiru-rostov006.ru
подключить домашний интернет ростов
вывод из запоя
vivod-iz-zapoya-chelyabinsk009.ru
лечение запоя челябинск
экстренный вывод из запоя
vivod-iz-zapoya-irkutsk008.ru
вывод из запоя круглосуточно
провайдеры по адресу санкт-петербург
inernetvkvartiru-spb004.ru
интернет провайдеры по адресу дома
вывод из запоя цена
vivod-iz-zapoya-cherepovec010.ru
вывод из запоя цена
вывод из запоя круглосуточно иркутск
vivod-iz-zapoya-irkutsk009.ru
вывод из запоя круглосуточно иркутск
подключение интернета санкт-петербург
inernetvkvartiru-spb005.ru
провайдеры интернета в санкт-петербурге
экстренный вывод из запоя
vivod-iz-zapoya-kaluga010.ru
вывод из запоя круглосуточно
номер наркологии [url=http://narkologicheskaya-klinika-13.ru]http://narkologicheskaya-klinika-13.ru[/url] .
наркологические клиники в москве [url=https://narkologicheskaya-klinika-14.ru]https://narkologicheskaya-klinika-14.ru[/url] .
локальное seo блог [url=https://blog-o-marketinge.ru/]blog-o-marketinge.ru[/url] .
Здравствуйте!
Резюме 2025: как не пролететь мимо работы мечты. [url=https://tvoya-sila-vnutri.ru/kak-sdelat-rezyume-na-rabotu/]Как сделать онлайн резюме[/url] Пошаговая инструкция создания резюме, которое пробьет любые ATS-системы и зацепит работодателя.
Читай тут: – https://tvoya-sila-vnutri.ru/kak-sdelat-rezyume-na-rabotu/
Как сделать резюме на работу
Покеда!
интернет провайдеры по адресу дома
inernetvkvartiru-spb006.ru
домашний интернет в санкт-петербурге
лечение запоя калуга
vivod-iz-zapoya-kaluga011.ru
вывод из запоя круглосуточно калуга
экстренный вывод из запоя череповец
vivod-iz-zapoya-cherepovec012.ru
вывод из запоя цена
лечение запоя
vivod-iz-zapoya-kaluga012.ru
вывод из запоя круглосуточно
подключить интернет
inernetvkvartiru-ekaterinburg004.ru
провайдеры интернета в екатеринбурге по адресу
статьи про маркетинг и seo [url=blog-o-marketinge1.ru]blog-o-marketinge1.ru[/url] .
Want to have fun? porno bangladesh melbet Watch porn, buy heroin or ecstasy. Pick up whores or buy marijuana. Come in, we’re waiting
Новые актуальные промокод iherb для первого заказа для выгодных покупок! Скидки на витамины, БАДы, косметику и товары для здоровья. Экономьте до 30% на заказах, используйте проверенные купоны и наслаждайтесь выгодным шопингом.
экстренный вывод из запоя
vivod-iz-zapoya-irkutsk007.ru
вывод из запоя круглосуточно
вывод из запоя круглосуточно
vivod-iz-zapoya-krasnodar011.ru
экстренный вывод из запоя
тарифы интернет и телевидение екатеринбург
inernetvkvartiru-ekaterinburg005.ru
интернет тарифы екатеринбург
экстренный вывод из запоя иркутск
vivod-iz-zapoya-irkutsk008.ru
лечение запоя
курсы seo [url=http://kursy-seo-1.ru/]http://kursy-seo-1.ru/[/url] .
seo курсы [url=http://www.kursy-seo-3.ru]seo курсы[/url] .
курс seo [url=http://www.kursy-seo-4.ru]http://www.kursy-seo-4.ru[/url] .
seo интенсив [url=https://www.kursy-seo-2.ru]https://www.kursy-seo-2.ru[/url] .
вывод из запоя цена
vivod-iz-zapoya-krasnodar012.ru
лечение запоя
интернет провайдеры екатеринбург по адресу
inernetvkvartiru-ekaterinburg006.ru
провайдеры екатеринбург
экстренный вывод из запоя
vivod-iz-zapoya-irkutsk009.ru
вывод из запоя цена
Добрый день!
Попрощался с работой не по своей воле? [url=https://zhit-legche.ru/chto-delat-esli-uvolili-s-raboty/]как пережить увольнение с работы форум[/url] Держи гайд по финансовому и психологическому выживанию.
Здесь подробней: – https://zhit-legche.ru/chto-delat-esli-uvolili-s-raboty/
как пережить несправедливое увольнение
что делать если уволили с работы
если вас уволили с работы
Будь здоров!
Хай!
Кредит под залог недвижимости с плохой кредиткой: реальные способы получить бабки. [url=https://kredit-bez-slov.ru/kredit-s-plohoj-istoriej-pod-zalog-nedvizhimosti/]кредит под залог недвижимости с плохой кредитной историей отзывы[/url] Честный разбор от своего в доску чувака.
Написал: – https://kredit-bez-slov.ru/kredit-s-plohoj-istoriej-pod-zalog-nedvizhimosti/
в каком банке можно взять кредит с плохой кредитной историей
Удачи!
экстренный вывод из запоя краснодар
vivod-iz-zapoya-krasnodar013.ru
вывод из запоя
HBet – Cổng giải trí trực tuyến hàng đầu, quy tụ hàng ngàn trò chơi cá cược thể thao, casino, slot game và bắn cá đổi thưởng. Giao diện mượt mà, bảo mật tuyệt …
plane crash game money [url=www.aviator-igra-1.ru/]www.aviator-igra-1.ru/[/url] .
провайдеры в красноярске по адресу проверить
inernetvkvartiru-krasnoyarsk004.ru
интернет провайдеры по адресу
статьи про продвижение сайтов [url=www.statyi-o-marketinge2.ru]статьи про продвижение сайтов[/url] .
вывод из запоя круглосуточно калуга
vivod-iz-zapoya-kaluga010.ru
экстренный вывод из запоя
интернет по адресу красноярск
inernetvkvartiru-krasnoyarsk005.ru
интернет провайдеры в красноярске по адресу дома
лечение запоя
vivod-iz-zapoya-kaluga011.ru
вывод из запоя круглосуточно калуга
plane crash money game [url=www.aviator-igra-2.ru/]www.aviator-igra-2.ru/[/url] .
игра авиатор ставки [url=http://aviator-igra-3.ru]игра авиатор ставки[/url] .
провайдеры по адресу красноярск
inernetvkvartiru-krasnoyarsk006.ru
какие провайдеры интернета есть по адресу красноярск
Электрокарниз — это идеальное решение для вашего дома, которое позволяет легко управлять шторами с помощью пульта.
Тем не менее, многие люди предпочитают устанавливать электрокарниз самостоятельно.
вывод из запоя
vivod-iz-zapoya-kaluga012.ru
экстренный вывод из запоя калуга
вывод из запоя круглосуточно
vivod-iz-zapoya-minsk007.ru
экстренный вывод из запоя минск
6907
Здарова!
Торговля игровыми профилями: сколько можно заработать и что за это будет. [url=https://zarabotok-na-igrah.ru/prodat-akkaunt-stim/]продать аккаунт стим[/url] Реальная статистика прибыли и потерь от практика.
Переходи: – https://zarabotok-na-igrah.ru/prodat-akkaunt-stim/
покупка аккаунтов стим
где продать стим аккаунт
Будь здоров!
Здравствуйте!
Сдаём анализ кала правильно: гайд для нормальных людей. [url=https://tvoya-sila-vnutri.ru/kak-sobrat-kal-na-analiz-lajfhak/]кал на анализ[/url] НиКаких медицинских заумностей, только практические советы и лайфхаки.
Читай тут: – https://tvoya-sila-vnutri.ru/kak-sobrat-kal-na-analiz-lajfhak/
Как правильно взять анализ кала
Пока!
Здравствуйте!
25 миллиардов в AI-токенах и это только начало. [url=https://pro-kriptu.ru/altkoiny-kotorye-dadut-iksy/]какие токены дадут иксы[/url] Fetch, Bittensor, Render – кто станет лидером сектора.
Написал: – https://pro-kriptu.ru/altkoiny-kotorye-dadut-iksy/
какие токены дадут иксы
как заработать на своем токене
альткоины которые вырастут
Бывай!
Откройте для себя удобство и стиль, используя [url=https://karniz-s-privodom.ru]карнизы с электроприводом|карнизы с электроприводом для штор|потолочные карнизы с электроприводом|карнизы с электроприводом и дистанционным управлением|карнизы с электроприводом цена|карнизы с электроприводом купить|карнизы с электроприводом с дистанционным управлением|карнизы с электроприводом и дистанционным|карнизы с электроприводом и пультом управления купить|Карнизы с электроприводом[/url] для вашего дома!
После установки, вы будете легко насладиться преимуществами электрокарнизов.
узнать интернет по адресу
inernetvkvartiru-krasnodar004.ru
провайдеры по адресу дома
вывод из запоя минск
vivod-iz-zapoya-minsk008.ru
вывод из запоя круглосуточно минск
вывод из запоя
vivod-iz-zapoya-krasnodar011.ru
экстренный вывод из запоя
1549
Электрические жалюзи [url=https://electroprivod-karniz.ru]электрические жалюзи на окна|электрические жалюзи с дистанционным управлением|электрические жалюзи на мансардные окна|купить электрические жалюзи на окна|электрические жалюзи в москве|электрические жалюзи автоматические|электрические жалюзи на пластиковые окна купить|электрические жалюзи стоимость|электрические жалюзи на окна заказать[/url] — это идеальное решение для современного интерьера, обеспечивающее комфорт и стиль.
Вы можете выбрать подходящий вариант, который гармонично впишется в ваш интерьер.
Здравствуйте!
Лучшие камерофоны 2025 года без маркетинговой лапши. [url=https://pro-telefony.ru/telefon-s-horoshej-kameroj/]бюджетный смартфон с хорошей камерой[/url] От бюджетников до флагманов – честный обзор от пацана к пацану.
Читай тут: – https://pro-telefony.ru/telefon-s-horoshej-kameroj/
samsung с хорошей камерой
Пока!
wettformat sportwetten bonus ohne einzahlung
Feel free to surf to my site darts wetten quoten
airplane money game [url=https://aviator-igra-4.ru/]https://aviator-igra-4.ru/[/url] .
изготовление проекта перепланировки [url=www.proekt-pereplanirovki-kvartiry8.ru]изготовление проекта перепланировки[/url] .
швейное производство под ключ [url=https://nitkapro.ru]https://nitkapro.ru[/url] .
проверить провайдера по адресу
inernetvkvartiru-krasnodar005.ru
интернет по адресу дома
7586
вывод из запоя круглосуточно
vivod-iz-zapoya-minsk009.ru
лечение запоя
Автоматические рулонные шторы не только обеспечивают удобство управления, но и стильный акцент в интерьере вашего дома, особенно если вы выберете [url=https://avtorulon.ru]автоматические рулонные шторы|автоматика для рулонных штор|автоматические шторы для труднодоступных окон[/url].
Во-вторых, их можно интегрировать в систему “умный дом”.
куплю диплом медсестры в москве [url=https://frei-diplom13.ru/]куплю диплом медсестры в москве[/url] .
В поисках достоверного источника редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем обширный каталог продукции, обеспечивая высочайшее качество каждого изделия.
Редметсплав.рф гарантирует все стадии сделки, предоставляя полный пакет необходимых документов для законного использования товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы выполнить любой запрос с прекрасным качеством обслуживания.
Наша команда службы поддержки всегда на связи, чтобы помочь вам в выборе товаров и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете уверенность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что наше качество и сервис – ваш лучший выбор.
поставляемая продукция:
Кольцо из драгоценных металлов платиновое 9х2х2 мм ПлРд90-10 ТУ Широкий выбор высококачественных кольц из драгоценных металлов. Элегантные украшения, созданные талантливыми мастерами. Уникальность и изысканность в каждой детали. Возможность заказа персонального кольца по вашим пожеланиям. Подчеркните свою индивидуальность с нашими кольцами.
РедМетСплав предлагает внушительный каталог отборных изделий из нестандартных материалов. Не важно, какие объемы вам необходимы – от мелких партий до обширных поставок, мы обеспечиваем своевременную реализацию вашего заказа.
Каждая единица продукции подтверждена соответствующими документами, подтверждающими их соответствие стандартам. Превосходное обслуживание – наша визитная карточка – мы на связи, чтобы ответить на ваши вопросы и находить ответы под требования вашего бизнеса.
Доверьте ваш запрос профессионалам РедМетСплав и убедитесь в широком спектре предлагаемых возможностей
Наши товары:
Поковка титановая ЭТ3 – ТУ 1-9-77-85 Лист титановый ЭТ3 – ТУ 1-9-77-85 представляет собой высококачественный металлический материал, обладающий отличной прочностью и коррозионной стойкостью. Этот лист идеален для использования в авиационной, медицинской и химической промышленности благодаря своим уникальным характеристикам. Лист титановый ЭТ3 – ТУ 1-9-77-85 легко поддается обработке и обладает низким весом, что делает его востребованным среди инженеров и конструкторов. Если вы хотите купить Лист титановый ЭТ3 – ТУ 1-9-77-85, обращайтесь к нам для получения консультаций и выгодных предложений. Мы обеспечим быструю доставку и конкурентные цены на данный продукт.
mega ссылка в тор https://dstw.ae
Официальная страница компании в сети : http://www.medtronik.ru/
[p][url=https://creditservice.ru.com/][b]SUNWIN[/b][/url] stands gone from as a in vogue online betting ecosystem built quest of players who value transparency, speed, and variety. From immersive [b]casino[/b] experiences to smart-number [b]x? s?[/b] systems and real-time [b]th? thao[/b] markets, the party line reflects unfathomable brains of digital wagering behavior in 2025. Fans of proficiency and betide can scrutinize crucial [b]trò choi[/b], fast-paced [b]game slots[/b], colorful [b]b?n cá[/b], and high-volatility [b]jackpot[/b] rounds. Routine favorites like [b]dá gà[/b], competitive [b]esports[/b], and table classics such as [b]baccarat[/b], [b]r?ng h?[/b], [b]tài x?u md5[/b], and [b]xóc dia[/b] are optimized instead of mobile-first play. What in fact elevates the familiarity is reactive [b]cskh[/b], humanitarian [b]khuy?n mãi[/b] and long-term [b]uu dãi[/b], benefit a withdraw [b]d?i lý[/b] house repayment for growth-focused partners. Discover more at [url=https://creditservice.ru.com/]https://creditservice.ru.com/[/url], where alteration meets reliability and every [b]n? hu[/b] note feels earned.[/p]
[b][url=https://creditservice.ru.com/]SUNWIN[/url][/b] is recognized as a modish online betting ecosystem where technology and passable looseness intersect. The dais delivers a full-bodied spectrum of pastime including [b]casino[/b], [b]x? s?[/b], [b]th? thao[/b], and interactive [b]trò choi[/b] designed for legitimate players. From immersive [b]game slots[/b], skill-based [b]b?n cá[/b], high-value [b]jackpot[/b], to routine [b]dá gà[/b] and competitive [b]esports[/b], the experience feels balanced and transparent. Flexible [b]khuy?n mãi[/b], sympathetic [b]cskh[/b], everyday [b]n? hu[/b], and unique [b]uu dãi[/b] support long-term job, while the [b]d?i lý[/b] methodology, provably kermis [b]tài x?u md5[/b], prototypical [b]xóc dia[/b], tangible [b]baccarat[/b], and fast-paced [b]r?ng h?[/b] over a data-driven betting environment. Official access: [url=https://creditservice.ru.com/]https://creditservice.ru.com/[/url].
[b][url=https://creditservice.ru.com/]SUNWIN[/url][/b] stands out as a trusted online stage where [b]casino[/b], [b]x? s?[/b], [b]th? thao[/b], and interactive [b]trò choi[/b] upon new-fashioned technology. From immersive [b]game slots[/b], fast-paced [b]b?n cá[/b], and high-value [b]jackpot[/b] events to competitive [b]dá gà[/b] and worldwide [b]esports[/b], the occurrence feels seamless and fair. Smart systems power [b]tài x?u md5[/b], [b]xóc dia[/b], [b]baccarat[/b], [b]r?ng h?[/b], and overwhelming [b]n? hu[/b]. With recurring [b]khuy?n mãi[/b], long-term [b]uu dãi[/b], efficient [b]cskh[/b], and willowy [b]d?i lý[/b] programs, players can explore confidently. Learn more at [url=https://creditservice.ru.com/]https://creditservice.ru.com/[/url].
send spam email
Email Bombing – email flood or email hoax (DOS attack) or cluster email bombing, what are they actually doing?
A huge number of emails are sent to e-mail. This usually means that the @Flood_email_bot specifically targets the victim’s mailbox associated with your email.
These emails are intended to make fun of friends or distract the victim from any security messages or other emails.
I am glad to present you a mail flood bot with a convenient menu and flexible settings!
The cost of the service is $ 1 = 1000 letters.
You specify the time of the flood and the number of letters yourself, or choose the “FAST FLOOD” function
During the flood, a sufficient number of letters arrive so that the owner would miss an important letter!
The bot will flood more than you ordered. On average, 30% more than ordered.
Flood email, Floods Email, Email flooding, gmail flood, email bomber, flood hotmail, flood online,email flooding, email flood bot, email flooded with spam, email flooding service, email flooded with subscriptions, email flooder bot, email bomber 2023, email bomber 2024, email spam bot online, email spammer bot free, spam bot, бот по флуду почт, сервис по флуду почт, услуги по флуду, флуд услуги.
@Flood_email_bot – Лучший емаил бомбер на рынке!
Experience Brainy https://askbrainy.com the free & open-source AI assistant. Get real-time web search, deep research, and voice message support directly on Telegram and the web. No subscriptions, just powerful answers.
casino rules casino elon
куплю диплом медсестры в москве [url=www.frei-diplom13.ru]куплю диплом медсестры в москве[/url] .
РедМетСплав предлагает широкий ассортимент качественных изделий из нестандартных материалов. Не важно, какие объемы вам необходимы – от мелких партий до масштабных поставок, мы обеспечиваем своевременную реализацию вашего заказа.
Каждая единица изделия подтверждена требуемыми документами, подтверждающими их соответствие стандартам. Опытная поддержка – наш стандарт – мы на связи, чтобы разрешать ваши вопросы по мере того как адаптировать решения под особенности вашего бизнеса.
Доверьте вашу потребность в редких металлах профессионалам РедМетСплав и убедитесь в множестве наших преимуществ
Наша продукция:
Полоса магниевая R60707 – UNS Порошок магниевый R60706 – UNS представляет собой высококачественный металл для различных промышленных применений. Этот продукт характеризуется отличной прочностью и легкостью, что делает его идеальным выбором для создания сплавов и других материалов. Порошок магниевый R60706 – UNS отлично подходит для использования в авиакосмической и автомобильной отраслях, обеспечивая надежность и долговечность. Если вы хотите улучшить характеристики своих изделий, купить Порошок магниевый R60706 – UNS станет разумным выбором. Этот порошок поможет вам достичь высоких стандартов качества в вашем производстве.
В поисках надежного поставщика редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем обширный каталог продукции, обеспечивая высочайшее качество каждого изделия.
Редметсплав.рф защищает все стадии сделки, предоставляя полный пакет необходимых документов для оформления товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы выполнить любой запрос с высоким уровнем сервиса.
Наша команда поддержки всегда на связи, чтобы помочь вам в подборе нужных изделий и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете достоверность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что наше качество и сервис – идеальный вариант для вас.
Наша продукция:
Поковка прямоугольная из конструкционной стали 300х1240 мм 45Х Конструкционная прямоугольная поковка – высококачественные материалы для создания прочных и надежных конструкций. Изготовленная из высококачественных материалов с применением передовых технологий, эта продукция обладает отличной прочностью, устойчивостью к износу, и находит широкое применение в машиностроении и строительстве.
Рабочий промокод всегда доступен на нашем сайте. Для поиска других вариантов можно воспользоваться любой поисковой системой, найти специализированную группу в социальных сетях или канал в мессенджерах (Viber, Telegram). Большинство ресурсов предоставляют актуальные промокоды Melbet, но стоит проверить при регистрации. Введите скопированный Melbet промокод на депозит и дождитесь уведомления от БК Мелбет, что бонус повышен. Помните, что второй раз зарегистрироваться и получить 50 000 рублей от Мелбет невозможно. При выборе поощрения по промокоду Мелбет существует поле «Отказаться от бонуса». В таком случае первое пополнение не увеличивается, и игрок может не следовать правилам вывода бонусных средств, а сразу делать именно те ставки, ради которых он и проходил регистрацию. Даже при отказе от бонусных средств рекомендуем ввести промокод Мелбет, так как в дальнейшем игрокам приходят специальные акции от Melbet. Помимо спортивной акции, игроки в казино также получать специальное предложение от БК. При использовании промокода Мелбет есть возможность получить бонус в казино до 125 000? и 290 фриспинов.
All Domains for Sell
Contact us : topnewsagency24x7@gmail.com
switzerlandnewstoday.com
maltanewstime.com
nationalposttoday.com
republicofchinatoday.com
russiannewstoday.com
crunchbasenewstoday.com
forbesnewstoday.com
livemintnewstoday.com
postgazettenewstoday.com
reuterstoday.com
themetronewstoday.com
huffingtonposttoday.com
neatherlandnewstoday.com
timesofnetherland.com
turkeynewstoday.com
walesnewstoday.com
australiannewstoday.com
bostonnewstoday.com
canadiannewstoday.com
cnbcnewstoday.com
mirrornewstoday.com
dwnewstoday.com
frenchnewstoday.com
guardiannewstoday.com
irishnewstoday.com
italiannewstoday.com
topworldnewstoday.com
washingtontimesnewstoday.com
scotlandnewstoday.com
chroniclenewstoday.com
britishnewstoday.com
loli girls tons vid pic
is.gd/BlCAHo
krtk.rs/e1i0ovy
РедМетСплав предлагает внушительный каталог высококачественных изделий из ценных материалов. Не важно, какие объемы вам необходимы – от мелких партий до крупных поставок, мы гарантируем быстрое выполнение вашего заказа.
Каждая единица продукции подтверждена всеми необходимыми документами, подтверждающими их происхождение. Опытная поддержка – наша визитная карточка – мы на связи, чтобы улаживать ваши вопросы и находить ответы под требования вашего бизнеса.
Доверьте вашу потребность в редких металлах специалистам РедМетСплав и убедитесь в множестве наших преимуществ
Наша продукция:
Проволока вольфрамовая ВТ-7 Проволока вольфрамовая ВТ-7 – это высококачественный материал, используемый в различных отраслях благодаря своим уникальным свойствам, таким как высокая температура плавления и прочность. Она идеально подходит для применения в электротехнике, сварке и производстве ламп. Эта проволока устойчива к коррозии и обеспечивает надежное соединение. Выбирая Проволоку вольфрамовую ВТ-7, вы получаете продукт, который соответствует самым жестким стандартам. Если вы хотите купить Проволока вольфрамовая ВТ-7, у нас есть широкий ассортимент этого товара. Закажите прямо сейчас и воспользуйтесь всеми преимуществами, которые она предлагает.
Good to be here!
I’m pretty new to this forum and figured to introduce myself.
Lately I’ve been researching outdoor projects lately and stumbled on several useful info.
For those with input on this topic, please know your feedback.
Cheers!
loli girls innumerable vid pic
is.gd/BlCAHo
krtk.rs/e1i0ovy
[p][url=https://sunwin.city/][b]SUNWIN[/b][/url] is a great extent recognized as a brand-new online betting ecosystem built in the service of players who value transparency and experience. From immersive [b]casino[/b] recreation and distinct [b]x? s?[/b] options to competitive [b]th? thao[/b] betting, the principles delivers balance between strategy and excitement. Gamers can traverse skill-based [b]trò choi[/b], fast-paced [b]game slots[/b], paradigmatic [b]b?n cá[/b], and high-reward [b]jackpot[/b] rooms designed with peaches RNG standards. Traditional Asian favorites such as [b]dá gà[/b], [b]tài x?u md5[/b], [b]xóc dia[/b], [b]baccarat[/b], [b]r?ng h?[/b], and [b]n? hu[/b] are optimized to save mechanical operate, while [b]esports[/b] betting reflects international 2025 trends. Eager [b]khuy?n mãi[/b], real-time [b]cskh[/b], alluring [b]uu dãi[/b], and a authority [b]d?i lý[/b] system steel long-term trust. Official access is elbow at [url=https://sunwin.city/]https://sunwin.city/[/url], ensuring players moor right away to the authoritative [b]SUNWIN[/b] environment.[/p]
Официальный сайт — переходи сейчас > https://kanctanta.ru/
[b][url=https://sunwin.city/]SUNWIN[/url][/b] is shaping the tomorrow of online betting in 2025 aside blending count on, help, and immersive entertainment. From a trendy [b]casino[/b] ecosystem to diversified options like [b]x? s?[/b], [b]th? thao[/b], and skill-based [b]trò choi[/b], the platform reflects lost insight into contestant behavior. Fans of [b]game slots[/b], [b]b?n cá[/b], and step by step [b]jackpot[/b] will warning sure payouts, while place markets such as [b]dá gà[/b], [b]esports[/b], [b]tài x?u md5[/b], [b]xóc dia[/b], [b]baccarat[/b], and [b]r?ng h?[/b] are optimized as real-time play. Key [b]khuy?n mãi[/b], long-term [b]uu dãi[/b], unmistakeable [b]d?i lý[/b] policies, and alive [b]cskh[/b] elevate user confidence. Proper access is close by at [url=https://sunwin.city/]https://sunwin.city/[/url], a pivot where [b]n? hu[/b] moments meet data-driven fairness.
[p][url=https://sunwin.city/][b]SUNWIN[/b][/url] is recognized nearby experienced players as a present-day core on online play, where [b]casino[/b] passion meets technology-driven trust. From paradigm [b]x? s?[/b] and competitive [b]th? thao[/b] betting to immersive [b]trò choi[/b] like [b]game slots[/b] and [b]b?n cá[/b], the dais reflects how digital wagering evolves in 2025. High-value [b]jackpot[/b] events, household [b]dá gà[/b], and fast-growing [b]esports[/b] markets allure miscellaneous audiences, while transparent systems such as [b]tài x?u md5[/b], [b]xóc dia[/b], [b]baccarat[/b], and [b]r?ng h?[/b] embellish fairness. Steady customer [b]khuy?n mãi[/b] and eliminating [b]uu dãi[/b] aid long-term on, backed not later than sensitive [b]cskh[/b] and a strong [b]d?i lý[/b] network. Accepted features like [b]n? hu[/b] total furor, making [url=https://sunwin.city/]https://sunwin.city/[/url] a notation item on players seeking rest between pageant and reliability.[/p]
[p][b][url=https://sunwin.city/]SUNWIN[/url][/b] is positioned as a modern focus quest of online [b]casino[/b] pageant, blending [b]x? s?[/b], [b]th? thao[/b], and interactive [b]trò choi[/b] into one seamless platform. From immersive [b]game slots[/b] and classic [b]b?n cá[/b] to high-reward [b]jackpot[/b] systems, users experience well-balanced carrying out and candid mechanics. Strategic fans delight in [b]dá gà[/b], competitive [b]esports[/b], and brisk betting like [b]tài x?u md5[/b], [b]xóc dia[/b], [b]baccarat[/b], and [b]r?ng h?[/b]. Iterative [b]khuy?n mãi[/b] and long-term [b]uu dãi[/b] buttress unwavering players, while able [b]cskh[/b] ensures velvety interaction. With scalable [b]d?i lý[/b] programs and overwhelming [b]n? hu[/b] events, the ecosystem reflects evolving user habits. Official access is many times verified at [url=https://sunwin.city/]https://sunwin.city/[/url].[/p]
[b][url=https://sunwin.city/]SUNWIN[/url][/b] is recognized as a exhaustive online betting ecosystem where [b]casino[/b] entertainment meets up to the minute technology. Players can study [b]x? s?[/b], glowing [b]th? thao[/b], interactive [b]trò choi[/b], immersive [b]game slots[/b], and venerable [b]b?n cá[/b] with frank systems. High-value [b]jackpot[/b] events, critical [b]dá gà[/b], competitive [b]esports[/b], and fair-play options like [b]tài x?u md5[/b], [b]xóc dia[/b], [b]baccarat[/b], and [b]r?ng h?[/b] appeal to well-versed users. Cooperative [b]khuy?n mãi[/b], reliable [b]cskh[/b], repeated [b]n? hu[/b], liberal [b]uu dãi[/b], and a transparent [b]d?i lý[/b] system define long-term trust. Recognized access is readily obtainable at [url=https://sunwin.city/]https://sunwin.city/[/url].
[b][url=https://sunwin.city/]SUNWIN[/url][/b] is positioned as a up to the minute hub in the interest of online presentation, combining percipient technology with trusted contestant demand in 2025. The principles delivers a gorged ecosystem of [b]casino[/b], [b]x? s?[/b], [b]th? thao[/b], and interactive [b]trò choi[/b] designed for speed, fairness, and immersion. From [b]game slots[/b], [b]b?n cá[/b], and explosive [b]jackpot[/b] rounds to strategic options like [b]baccarat[/b], [b]r?ng h?[/b], [b]xóc dia[/b], [b]tài x?u md5[/b], and [b]dá gà[/b], every occurrence is optimized an eye to real-time engagement. Competitive fans can investigate [b]esports[/b], while value seekers extras from frequent [b]khuy?n mãi[/b] and long-term [b]uu dãi[/b]. With open [b]cskh[/b], candid payouts, excepting [b]n? hu[/b] events, and a scalable [b]d?i lý[/b] system, users can access the whole right away at [url=https://sunwin.city/]https://sunwin.city/[/url].
[p][url=https://sunwin.city/][b]SUNWIN[/b][/url] stands antiquated in the new online betting store by way of combining transparency, speed, and exhibition into a man seamless platform. From immersive [b]casino[/b] experiences to fair-play [b]x? s?[/b] systems, the stand reflects deep percipience into digital wagering behavior. Sports lovers delight in distinct [b]th? thao[/b] options, while casual users inquire interactive [b]trò choi[/b] such as [b]game slots[/b], [b]b?n cá[/b], [b]n? hu[/b], and high-reward [b]jackpot[/b] rooms. Cardinal players can test skills with [b]dá gà[/b], [b]esports[/b], [b]tài x?u md5[/b], [b]xóc dia[/b], [b]baccarat[/b], and [b]r?ng h?[/b]. Regular [b]khuy?n mãi[/b] and long-term [b]uu dãi[/b] are supported not later than reactive [b]cskh[/b] and a transpicuous [b]d?i lý[/b] system. Ferret out the fully ecosystem at [url=https://sunwin.city/]https://sunwin.city/[/url] and happening a podium designed representing trust, fulfilment, and innovation.[/p]
[p]
[b][url=https://sunwin.city/]SUNWIN[/url][/b] has emerged as a trusted target in the smashing of online wagering, blending invention with dependable play. The policy delivers a do ecosystem covering [b]casino[/b], [b]x? s?[/b], [b]th? thao[/b], and interactive [b]trò choi[/b] designed to make off to modern users. From immersive [b]game slots[/b] and skill-based [b]b?n cá[/b] to high-reward [b]jackpot[/b] systems, every quality reflects a abyssal mastery of of trouper behavior. Fans of competitive consciousness can explore [b]dá gà[/b], [b]esports[/b], and esteemed tables like [b]baccarat[/b], [b]r?ng h?[/b], [b]xóc dia[/b], and [b]tài x?u md5[/b]. With pellucid [b]khuy?n mãi[/b], harmless [b]cskh[/b], good-looking [b]uu dãi[/b], and a persistent [b]d?i lý[/b] network, [b]SUNWIN[/b] continues to send benchmarks. Documented access is accessible at [url=https://sunwin.city/]https://sunwin.city/[/url], where verify meets technology-driven fairness.
[/p]
teensy-weensy girls diversified vid pic
is.gd/BlCAHo
krtk.rs/e1i0ovy
[p][url=https://sunwin.city/][b]SUNWIN[/b][/url] represents a modern betting ecosystem built an eye to players who value positiveness and alteration in online wagering. From immersive [b]casino[/b] experiences to energetic [b]x? s?[/b] draws, competitive [b]th? thao[/b] markets, and skill-based [b]trò choi[/b], the policy balances play with transparency. Popular options like [b]game slots[/b], [b]b?n cá[/b], [b]jackpot[/b], [b]dá gà[/b], and [b]esports[/b] are supported by iterative [b]khuy?n mãi[/b], communicative [b]cskh[/b], and fair-play systems. Advanced modes such as [b]n? hu[/b], [b]tài x?u md5[/b], [b]xóc dia[/b], [b]baccarat[/b], and [b]r?ng h?[/b] reflect astute manufacture awareness, while [b]uu dãi[/b] programs and a growing [b]d?i lý[/b] network enhance long-term value. Learn more at [url=https://sunwin.city/]https://sunwin.city/[/url].[/p]
Here’s the newest update
[b][url=https://sunwin.city/]SUNWIN[/url][/b] is shaping a advanced touchstone in online entertainment by combining [b]casino[/b], [b]x? s?[/b], [b]th? thao[/b], and immersive [b]trò choi[/b] on single seamless platform. From cardinal [b]game slots[/b] and skill-based [b]b?n cá[/b] to high-reward [b]jackpot[/b], exemplary [b]baccarat[/b], [b]r?ng h?[/b], and fair-play [b]tài x?u md5[/b], every attribute is built for transparency and speed. Fans of [b]dá gà[/b] and competitive [b]esports[/b] resolve know real-time information and slick odds. Dogmatic [b]cskh[/b], tensile [b]khuy?n mãi[/b], long-term [b]uu dãi[/b], and a take [b]d?i lý[/b] technique betray a impenetrable reconciliation of trouper needs. Explore more at [url=https://sunwin.city/]https://sunwin.city/[/url].
РедМетСплав предлагает обширный выбор отборных изделий из нестандартных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до крупных поставок, мы обеспечиваем быстрое выполнение вашего заказа.
Каждая единица изделия подтверждена требуемыми документами, подтверждающими их происхождение. Превосходное обслуживание – наша визитная карточка – мы на связи, чтобы разрешать ваши вопросы и находить ответы под требования вашего бизнеса.
Доверьте ваш запрос специалистам РедМетСплав и убедитесь в множестве наших преимуществ
поставляемая продукция:
Пруток магниевый Coralloy Zirconium 704 – KIND & CO., Edelstahlwerk, KG Проволока магниевая Coralloy Zirconium 704 – KIND & CO., Edelstahlwerk, KG – это высококачественный материал, предназначенный для сварки и других производственных процессов. Обладая отличными антикоррозийными свойствами, она обеспечивает надежность соединений даже в самых сложных условиях. Благодаря своей высокой прочности, проволока подходит для применения в автомобильной, аэрокосмической и строительной отраслях.Если вы хотите выбрать лучшее для своего проекта, не упустите возможность купить Проволока магниевая Coralloy Zirconium 704 – KIND & CO., Edelstahlwerk, KG. Этот продукт станет вашим надежным помощником в достижении высококачественного результата.
Equilibrado de piezas
El equilibrado representa una fase clave en las tareas de mantenimiento de maquinaria agricola, asi como en la fabricacion de ejes, volantes, rotores y armaduras de motores electricos. El desequilibrio genera vibraciones que incrementan el desgaste de los rodamientos, generan sobrecalentamiento e incluso pueden causar la rotura de los componentes. Con el fin de prevenir fallos mecanicos, es fundamental identificar y corregir el desequilibrio de forma temprana utilizando tecnicas modernas de diagnostico.
Principales metodos de equilibrado
Hay diferentes tecnicas para corregir el desequilibrio, dependiendo del tipo de componente y la magnitud de las vibraciones:
El equilibrado dinamico – Se utiliza en componentes rotativos (rotores y ejes) y se realiza en maquinas equilibradoras especializadas.
El equilibrado estatico – Se usa en volantes, ruedas y otras piezas donde basta con compensar el peso en un solo plano.
Correccion del desequilibrio – Se realiza mediante:
Taladrado (retirada de material en la zona de mayor peso),
Instalacion de contrapesos (en ruedas y aros de volantes),
Ajuste de masas de balanceo (por ejemplo, en ciguenales).
Diagnostico del desequilibrio: ?que equipos se utilizan?
Para detectar con precision las vibraciones y el desequilibrio, se utilizan:
Maquinas equilibradoras – Permiten medir el nivel de vibracion y determinan con exactitud los puntos de correccion.
Equipos analizadores de vibraciones – Capturan el espectro de oscilaciones, detectando no solo el desequilibrio, sino tambien otros defectos (como el desgaste de rodamientos).
Sistemas laser – Se usan para mediciones de alta precision en componentes criticos.
Especial atencion merecen las velocidades criticas de rotacion – regimenes en los que la vibracion aumenta drasticamente debido a fenomenos de resonancia. Un equilibrado correcto previene danos en el equipo bajo estas condiciones.
где можно купить диплом медсестры [url=https://frei-diplom13.ru/]где можно купить диплом медсестры[/url] .
?Necesitas mudarte? https://trasladoavalencia.es ?Necesitas una mudanza rapida, segura y sin complicaciones en Valencia? Ofrecemos servicios profesionales de transporte y mudanzas para particulares y empresas. ?Solicita un presupuesto gratuito y disfruta de nuestro servicio de calidad!
РедМетСплав предлагает обширный выбор отборных изделий из ценных материалов. Не важно, какие объемы вам необходимы – от мелких партий до крупных поставок, мы гарантируем быстрое выполнение вашего заказа.
Каждая единица товара подтверждена соответствующими документами, подтверждающими их качество. Дружелюбная помощь – наш стандарт – мы на связи, чтобы разрешать ваши вопросы а также находить ответы под особенности вашего бизнеса.
Доверьте вашу потребность в редких металлах специалистам РедМетСплав и убедитесь в широком спектре предлагаемых возможностей
Наши товары:
Круг ниобиевый НбП-1б – ГОСТ 26252-84 Круг ниобиевый НбП-1б – ГОСТ 26252-84 представляет собой высококачественный металлургический продукт, используемый в различных отраслях промышленности. Этот ниобиевый круг обеспечивает отличные механические свойства и имеет высокую коррозионную стойкость. Он идеально подходит для производства компонентов, требующих надежности и долговечности. Купить Круг ниобиевый НбП-1б – ГОСТ 26252-84 значит обеспечить свой проект высокопрочным материалом, который прослужит долго. Применяйте его в своих производственных процессах и убедитесь в его превосходных качествах!
Промокод 1xBet на сегодня при регистрации. Новички могут использовать промокоды для получения различных бонусов от букмекера. Доступ к кодам есть на тематических сайтах и рабочих зеркалах. 1xbet предлагает разные способы регистрации: в 1 клик. Компания заботится о клиентах и соблюдает международное право. Актуальные промокод 1xBet для старых игроков можно получить бесплатно: на нашем сайте. Любой желающий легко найдёт промокод 1xbet на сегодня. Бонусы щедрые, а условия их получения — реальные. В некоторых случаях вообще ничего делать не нужно.
Personally discovered this Astronaut multiplier gameplay a few days ago and this game completely grabbed my attention, link https://crushtop.org . The mechanic is basic: a astronaut goes forward while a multiplier grows, and I need to stop prior to the fail. Bigger volatility equals bigger profit, so decision-making becomes critical.
Initially I started minimal, mainly so I could learn the mechanic, but in several bets I noticed the rhythm. The adrenaline gets insane single moment, especially as the number continues going up. This layout feels minimalistic, nothing important confuses, and the whole game works fast.
I also played from my phone and it ran perfectly. Cashouts were instant, which is critical personally. I haven’t seen anything strange at all. To sum it up, this Astronaut crash experience is engaging. If someone enjoy fast casino games, this is worth playing.
Just keep in mind: play smart.
Получить диплом о высшем образовании можем помочь. Купить диплом магистра в Ставрополе – [url=http://diplomybox.com/kupit-diplom-magistra-v-stavropole/]diplomybox.com/kupit-diplom-magistra-v-stavropole[/url]
Hey all!
I am new to the community and wanted I’d say hello.
I’ve been exploring yard improvements these days and found several helpful tips.
If you have expertise in this area, I’d like to read your thoughts.
Thanks!
купить медицинский диплом медсестры [url=http://frei-diplom13.ru/]купить медицинский диплом медсестры[/url] .
РедМетСплав предлагает внушительный каталог отборных изделий из ценных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до обширных поставок, мы обеспечиваем своевременную реализацию вашего заказа.
Каждая единица продукции подтверждена требуемыми документами, подтверждающими их происхождение. Превосходное обслуживание – наша визитная карточка – мы на связи, чтобы улаживать ваши вопросы а также находить ответы под особенности вашего бизнеса.
Доверьте потребности вашего бизнеса специалистам РедМетСплав и убедитесь в множестве наших преимуществ
поставляемая продукция:
Магний AM20HP Магний AM20HP – это высококачественная добавка, разработанная для поддержания нормального уровня магния в организме. Он способствует улучшению обмена веществ, поддерживает здоровье мышечной и нервной систем. Данная форма магния легко усваивается и не вызывает неприятных ощущений в желудке.Если вы хотите укрепить свое здоровье и улучшить общее самочувствие, купить Магний AM20HP – это правильное решение. Применяйте его для восстановления минерального баланса и повышения энергетического уровня. Не упустите возможность сделать шаг к более здоровой жизни!
Great advice! I’ll definitely be implementing some of these tips.
Your analysis has changed how I think entirely.
сколько стоит купить диплом медсестры [url=www.frei-diplom13.ru]сколько стоит купить диплом медсестры[/url] .
1xBet промокод Используйте на https://cere-india.org/art/code_promotionnel_21.html и получите 100% к первому депозиту до 32 500?, чтобы начать игру с преимуществом.
Мы предлагаем дипломы психологов, юристов, экономистов и прочих профессий по приятным тарифам. Стоимость зависит от выбранной специальности, года получения и образовательного учреждения: [url=http://demo.zealousweb.com/wordpress-plugins/accept-stripe-payments-using-contact-form-7/?p=2778/]demo.zealousweb.com/wordpress-plugins/accept-stripe-payments-using-contact-form-7/?p=2778[/url]
Мы предлагаем дипломы любых профессий по приятным ценам. Быстро и просто купить диплом о высшем образовании [url=http://homesbycosette.com/agents/elmosiegel9700/]homesbycosette.com/agents/elmosiegel9700[/url]
Мы изготавливаем дипломы любых профессий по доступным тарифам. Диплом о получении высшего образования когда-то считался главным документом, который способствовал успешному поиску работы. Выгодно заказать диплом института!: [url=http://app.webtoseo.com/2025/12/26/diplom-za-korotkij-srok-sroki-ceny-uslovija-284/]app.webtoseo.com/2025/12/26/diplom-za-korotkij-srok-sroki-ceny-uslovija-284[/url]
Приобрести диплом ВУЗа по доступной стоимости возможно, обращаясь к проверенной специализированной компании. Для проверки компании до покупки воспользуйтесь отзывами на форумах. Можно заказать диплом из любого института РФ [url=http://news1.listbb.ru/viewtopic.php?f=3&t=4680/]news1.listbb.ru/viewtopic.php?f=3&t=4680[/url]
РедМетСплав предлагает широкий ассортимент отборных изделий из редких материалов. Не важно, какие объемы вам необходимы – от мелких партий до масштабных поставок, мы обеспечиваем быстрое выполнение вашего заказа.
Каждая единица товара подтверждена требуемыми документами, подтверждающими их качество. Дружелюбная помощь – наш стандарт – мы на связи, чтобы улаживать ваши вопросы и находить ответы под особенности вашего бизнеса.
Доверьте ваш запрос специалистам РедМетСплав и убедитесь в множестве наших преимуществ
Наши товары:
Пруток висмутовый Sn96Ag2,5Bi1Cu,5 – IEC 61190-1-3 Пруток висмутовый Sn96Ag2,5Bi1Cu,5 – IEC 61190-1-3 – это идеальное решение для высококачественной пайки. Состав этого прутка включает 96% олова, 2,5% серебра, 1% висмута и 0,5% меди, что обеспечивает отличную теплопроводность и стойкость к окислению. Он соответствует международным стандартам, что гарантирует надежность. Если вы ищете надежный материал для электроники, не упустите возможность купить Пруток висмутовый Sn96Ag2,5Bi1Cu,5 – IEC 61190-1-3. Этот продукт идеально подходит для профессионалов и любителей. Убедитесь в его высоких характеристиках уже сегодня!
Мы готовы предложить дипломы любой профессии по приятным тарифам.– [url=http://school8kaluga.flybb.ru/viewtopic.php?f=19&t=1273/]school8kaluga.flybb.ru/viewtopic.php?f=19&t=1273[/url]
Seriously quite a lot of wonderful data.
luxury casino canada great canadian casino vancouver best casino canada
Equilibrado de piezas
El equilibrado representa una fase clave en el mantenimiento de maquinaria agricola, asi como en la produccion de ejes, volantes, rotores y armaduras de motores electricos. Un desequilibrio provoca vibraciones que incrementan el desgaste de los rodamientos, generan sobrecalentamiento e incluso pueden causar la rotura de los componentes. Con el fin de prevenir fallos mecanicos, es fundamental identificar y corregir el desequilibrio de forma temprana utilizando metodos modernos de diagnostico.
Principales metodos de equilibrado
Existen varias tecnicas para corregir el desequilibrio, dependiendo del tipo de pieza y la magnitud de las vibraciones:
Equilibrado dinamico – Se utiliza en componentes rotativos (rotores y ejes) y se realiza en maquinas equilibradoras especializadas.
Equilibrado estatico – Se emplea en volantes, ruedas y piezas similares donde es suficiente compensar el peso en un unico plano.
La correccion del desequilibrio – Se realiza mediante:
Taladrado (retirada de material en la zona de mayor peso),
Instalacion de contrapesos (en ruedas, aros de volantes),
Ajuste de masas de equilibrado (como en el caso de los ciguenales).
Diagnostico del desequilibrio: ?que equipos se utilizan?
Para detectar con precision las vibraciones y el desequilibrio, se utilizan:
Equipos equilibradores – Miden el nivel de vibracion y determinan con exactitud los puntos de correccion.
Equipos analizadores de vibraciones – Capturan el espectro de oscilaciones, detectando no solo el desequilibrio, sino tambien fallos adicionales (como el desgaste de rodamientos).
Sistemas laser – Se emplean para mediciones de alta precision en mecanismos criticos.
Especial atencion merecen las velocidades criticas de rotacion – regimenes en los que la vibracion aumenta drasticamente debido a la resonancia. Un equilibrado adecuado evita danos en el equipo bajo estas condiciones.
need a video? video production services in milan offering full-cycle services: concept, scripting, filming, editing and post-production. Commercials, corporate videos, social media content and branded storytelling. Professional crew, modern equipment and a creative approach tailored to your goals.
https://alstr.in/mOpQw
Официальный сайт букмекерской компании
куплю диплом медсестры в москве [url=frei-diplom13.ru]куплю диплом медсестры в москве[/url] .
https://www.elbh.cz/hotel/view.php?id=aHR0cHM6Ly9ib29rcy5nb29nbGUuZnIvYm9va3M/aWQ9LVNHYkVRQUFRQkFK
Мы изготавливаем дипломы любой профессии по доступным ценам. Цена зависит от определенной специальности, года получения и образовательного учреждения: [url=http://hoiphelieu.com/companies/diploman-doku/]hoiphelieu.com/companies/diploman-doku[/url]
РедМетСплав предлагает обширный выбор качественных изделий из нестандартных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до масштабных поставок, мы гарантируем быстрое выполнение вашего заказа.
Каждая единица изделия подтверждена всеми необходимыми документами, подтверждающими их происхождение. Опытная поддержка – наш стандарт – мы на связи, чтобы улаживать ваши вопросы и адаптировать решения под особенности вашего бизнеса.
Доверьте ваш запрос специалистам РедМетСплав и убедитесь в множестве наших преимуществ
Наши товары:
Пруток вольфрамовый W-T20 Пруток вольфрамовый W-T20 – это высококачественный материал, используемый в различных промышленных областях. Его уникальные свойства, такие как высокая температура плавления и отличная устойчивость к окислению, делают его незаменимым для производства электродов, также для радиационной защиты и других специализированных применений. Если вы ищете надежный и долговечный материал для своих проектов, то вам стоит купить Пруток вольфрамовый W-T20. Он обеспечит высокую производительность и эффективность в работе. Выбирайте качество и надежность – выберите пруток, который отвечает всем современным требованиям.
Мы изготавливаем дипломы психологов, юристов, экономистов и прочих профессий по приятным тарифам. Диплом об образовании когда-то считался основным документом, который способствовал удачному поиску работы. Заказать диплом о высшем образовании!: [url=http://hlcsac.com/noticias/diplom-za-korotkij-srok-sroki-ceny-uslovija-291/]hlcsac.com/noticias/diplom-za-korotkij-srok-sroki-ceny-uslovija-291[/url]
gay anal vibrator
Приобрести диплом университета по невысокой стоимости можно, обращаясь к проверенной специализированной компании. Чтобы проверить компанию до заказа пользуйтесь рейтингом и отзывами на форумах. Можно приобрести диплом из любого университета РФ [url=http://rilezzz.com/read-blog/30312_kupit-diplom-o-vysshem-obrazovanii.html/]rilezzz.com/read-blog/30312_kupit-diplom-o-vysshem-obrazovanii.html[/url]
Продажа тяговых https://faamru.com аккумуляторных батарей для вилочных погрузчиков, ричтраков, электротележек и штабелеров. Решения для интенсивной складской работы: стабильная мощность, долгий ресурс, надёжная работа в сменном режиме, помощь с подбором АКБ по параметрам техники и оперативная поставка под задачу
If you follow the Russian-language streaming scene, you’ve likely heard about the Mellstroy Game project. This isn’t just another online casino, but a full-fledged gaming ecosystem announced and actively promoted by a popular streamer. The website [url=https://jobhop.co.uk/blog/408770/———-480]mellstroy game[/url] offers a detailed look at the infrastructure technical implementation, licensing, and current bonus terms. The core of the project is a synthesis of entertainment amount and classic betting, where stream viewers can not only watch the gameplay but also participate directly through integrated mechanics.
An analysis of the game lobby reveals a serious approach to proportion and classic speculation curation. The infrastructure partners with leading providers like NetEnt, Pragmatic Play, and Evolution Gaming, ensuring fair Return to Player (RTP) rates for slots and table games. It’s crucial to distinguish between the RTP of a specific slot machine and the casino’s overall theoretical profitability—these are different financial metrics. For example, slots like Book of Dead often feature an RTP around 96%, which is benchmark for quality products. In the live casino section, you’ll find not only blackjack and roulette but also options rare in the Russian-speaking market, such as Dragon Tiger or Lightning Roulette with enhanced multipliers.
Financial transactions are a critically important aspect for any visitor. Mellstroy Game offers a grade market set of payment systems: from VISA/Mastercard bank cards to e-wallets and cryptocurrencies. Pay close attention to the account verification policy. It complies with KYC (Know Your Customer) standards and requires document submission for withdrawing large sums. This isn’t a whim but a requirement of international regulators aimed at combating money laundering. Withdrawal fees vary depending on the method and can be offset by meeting wagering requirements.
The bonus program requires detailed study. A welcome package, typically split across several deposits, usually comes with high wagering requirements (x40-x50). Such a wagering multiplier is typical for aggressive marketing offers. From a practical standpoint, weekly cashback promotions or tournaments with prize pools might offer more value, providing higher chances of a real win. Always read the full terms and conditions of promotions, especially clauses about maximum bet sizes while wagering a promotion and the list of eligible games.
The technical side is implemented on a responsive system. The interface displays correctly on mobile devices without the need to download a separate app, saving memory and providing instant access via a browser. Modern SSL encryption is used to protect transaction data. To circumvent potential provider blocks, a working mirror site is provided; the current link can be found in the project’s official Telegram channel. This is specification practice for maintaining stable access.
Safety and responsible gaming are the foundation of trust. Holding a Curacao eGaming license means the operator is obligated to provide players with tools for self-control: setting deposit limits, taking gameplay breaks, or self-exclusion. Ignoring these tools is unwise. It’s also important to understand that despite the involvement of a media personality, a casino is a business with a mathematical edge (house advantage). Streams showcasing large wins are part of the marketing method, not a guide to action.
The final finding on the Mellstroy Game project is nuanced. On one hand, it’s a professionally assembled framework with a license, a strong provider pool, and thoughtful logistics. On the other hand, it exists in an aggressive competitive field, where its key differentiator is its connection to the founder’s persona. This introduces specific risks related to reputational fluctuations. For an experienced player evaluating a casino through the lens of mathematics, technical reliability, and withdrawal conditions, the platform presents certain interest. Beginners, however, should first study the basic principles of wagering, probability theory, and only then consider making a deposit, strictly based on their entertainment budget, not on expectations of quick profit.
http://www.ennnewenergy.com/index.php?route=common/language/language&languagelist=zh-cn&redirectlan=aHR0cHM6Ly9ib29rcy5nb29nbGUuZnIvYm9va3M/aWQ9LVNHYkVRQUFRQkFK
Продажа тяговых https://ab-resurs.ru аккумуляторных батарей для вилочных погрузчиков и штабелеров. Надёжные решения для стабильной работы складской техники: большой выбор АКБ, профессиональный подбор по параметрам, консультации специалистов, гарантия и оперативная поставка для складов и производств по всей России
https://bitgg.co/o5eYBA
リアル ラブドールpor Ioāō de Barreyra empressor da Universidade.Comprivilegio Real que nenhūa pessoa a possa imprimir,
If you want to receive the exclusive betwinner welcome bonus, go to https://bet-promo-codes.com/sportsbook-reviews/betwinner-registration/ and fill in your details during registration. The reward will be credited after your first deposit.
Посети официальный сайт компании : https://www.res-rent.ru/img/pages/1xbet-promokod-pri-registracii-besplatno.html
На этом ресурсе здесь работает kraken маркетплейс вход через все доступные официальные зеркала площадки
куплю диплом младшей медсестры [url=https://frei-diplom13.ru/]https://frei-diplom13.ru/[/url] .
http://cl.angel.wwx.tw/debug/frm-s/film-13.ru/article?ouqfcmb
Very well voiced really. !
best usa online casinos [url=https://bhcmerced.org/#]casino live online[/url]
РедМетСплав предлагает внушительный каталог качественных изделий из нестандартных материалов. Не важно, какие объемы вам необходимы – от мелких партий до масштабных поставок, мы гарантируем своевременную реализацию вашего заказа.
Каждая единица товара подтверждена соответствующими документами, подтверждающими их соответствие стандартам. Дружелюбная помощь – наша визитная карточка – мы на связи, чтобы улаживать ваши вопросы и находить ответы под особенности вашего бизнеса.
Доверьте вашу потребность в редких металлах профессионалам РедМетСплав и убедитесь в множестве наших преимуществ
поставляемая продукция:
Пруток магниевый AZ61A – WW T-825B Проволока магниевая AZ61A – WW T-825B является идеальным выбором для монтажа и ремонта. Этот высококачественный материал обеспечивает надежность и отличные механические свойства. Благодаря составу AZ61A, проволока отличается хорошей свариваемостью и коррозионной стойкостью. Ее применяют в различных областях, включая автомобилестроение и авиацию. Не упустите шанс купить Проволока магниевая AZ61A – WW T-825B для своих проектов и обеспечьте долговечность конструкций. Этот продукт станет незаменимым помощником для профессионалов и любителей!
Продажа тяговых faamru.com аккумуляторных батарей для вилочных погрузчиков, ричтраков, электротележек и штабелеров. Решения для интенсивной складской работы: стабильная мощность, долгий ресурс, надёжная работа в сменном режиме, помощь с подбором АКБ по параметрам техники и оперативная поставка под задачу
If you follow the Russian-language streaming scene, you’ve likely heard about the Mellstroy Game project. This isn’t just another online casino, but a full-fledged gaming ecosystem announced and actively promoted by a popular streamer. The website [url=https://jobhop.co.uk/blog/408770/———-480]mellstroy game[/url] offers a detailed look at the environment technical implementation, licensing, and current bonus terms. The core of the project is a synthesis of entertainment volume and classic wagering, where stream viewers can not only watch the gameplay but also participate directly through integrated mechanics.
An analysis of the game lobby reveals a serious approach to elements and classic speculation curation. The infrastructure partners with leading providers like NetEnt, Pragmatic Play, and Evolution Gaming, ensuring fair Return to Player (RTP) rates for slots and table games. It’s crucial to distinguish between the RTP of a specific slot machine and the casino’s overall theoretical profitability—these are different financial metrics. For example, slots like Book of Dead often feature an RTP around 96%, which is grade for quality products. In the live casino section, you’ll find not only blackjack and roulette but also options rare in the Russian-speaking market, such as Dragon Tiger or Lightning Roulette with enhanced multipliers.
Financial transactions are a critically important aspect for any patron. Mellstroy Game offers a convention market set of payment systems: from VISA/Mastercard bank cards to e-wallets and cryptocurrencies. Pay close attention to the account verification policy. It complies with KYC (Know Your Customer) standards and requires document submission for withdrawing large sums. This isn’t a whim but a requirement of international regulators aimed at combating money laundering. Withdrawal fees vary depending on the method and can be offset by meeting wagering requirements.
The incentive program requires detailed study. A welcome package, typically split across several deposits, usually comes with high wagering requirements (x40-x50). Such a wagering multiplier is typical for aggressive marketing offers. From a practical standpoint, weekly cashback promotions or tournaments with prize pools might offer more value, providing higher chances of a real win. Always read the full terms and conditions of promotions, especially clauses about maximum bet sizes while wagering a incentive and the list of eligible games.
The technical side is implemented on a responsive environment. The interface displays correctly on mobile devices without the need to download a separate app, saving memory and providing instant access via a browser. Modern SSL encryption is used to protect transaction data. To circumvent potential provider blocks, a working mirror site is provided; the current link can be found in the project’s official Telegram channel. This is model practice for maintaining stable access.
Safety and responsible gaming are the foundation of trust. Holding a Curacao eGaming license means the operator is obligated to provide players with tools for self-control: setting deposit limits, taking gameplay breaks, or self-exclusion. Ignoring these tools is unwise. It’s also important to understand that despite the involvement of a media personality, a casino is a business with a mathematical edge (house advantage). Streams showcasing large wins are part of the marketing plan, not a guide to action.
The final verdict on the Mellstroy Game project is nuanced. On one hand, it’s a professionally assembled environment with a license, a strong provider pool, and thoughtful logistics. On the other hand, it exists in an aggressive competitive field, where its key differentiator is its connection to the founder’s persona. This introduces specific risks related to reputational fluctuations. For an experienced contender evaluating a casino through the lens of mathematics, technical reliability, and withdrawal conditions, the system presents certain interest. Beginners, however, should first study the basic principles of speculation, probability theory, and only then consider making a deposit, strictly based on their entertainment budget, not on expectations of quick profit.
дивитися серіали кримінальні серіали дивитися онлайн
комедії онлайн якості серіали 2026 дивитися онлайн безкоштовно
Great post! If you are suddenly looking for something elegant for the winter, [url=https://mekhov.com/shubi-turtsiya-standarti-kachestva/][color=#1C1C1C]Turkish fur coats deserve attention.[/color][/url]
можно ли купить диплом медсестры [url=http://frei-diplom13.ru]можно ли купить диплом медсестры[/url] .
Мы изготавливаем дипломы любой профессии по выгодным ценам. Цена может зависеть от той или иной специальности, года получения и образовательного учреждения: [url=http://avtoweek2016.ru/dokumentyi-dlya-rabotyi-kogda-bez-diploma-nikuda/]avtoweek2016.ru/dokumentyi-dlya-rabotyi-kogda-bez-diploma-nikuda[/url]
Informationbreach – Your Email May Already Be Exposed
Your inbox isn’t safe anymore. Hackers mail, stolen logins, and email vulnerability are spreading fast — and your email address on the dark web could be the next target.
Informationbreach scans 33B+ breached passwords and 50M new records daily to reveal if your account has been compromised. Instantly check email in dark web, detect hack email account attempts, and verify credentials security before damage happens.
Run a real-time exposure check, see if someone has hacked into your email, and secure your identity with accurate results — not guesses.
Full access is just $2 — unlock everything, stay protected, and take control before hackers do.
Scan Email Now: [url=https://informationbreach.net] Email address exposed on dark web[/url]
|
Мы предлагаем дипломы любой профессии по выгодным тарифам. Диплом об образовании прежде считался главным документом, способствовавшим удачному поиску работы. Заказать диплом о высшем образовании!: [url=http://wikipedia.rapidnodes.net/index.php?title=User:Leandra12I/]wikipedia.rapidnodes.net/index.php?title=User:Leandra12I[/url]
накрутка подписчиков телеграм
Мы изготавливаем дипломы любой профессии по разумным тарифам. Заказать диплом об образовании [url=http://povzroslomu.kabb.ru/viewtopic.php?f=3&t=2137/]povzroslomu.kabb.ru/viewtopic.php?f=3&t=2137[/url]
РедМетСплав предлагает обширный выбор отборных изделий из редких материалов. Не важно, какие объемы вам необходимы – от небольших закупок до масштабных поставок, мы обеспечиваем быстрое выполнение вашего заказа.
Каждая единица товара подтверждена всеми необходимыми документами, подтверждающими их происхождение. Дружелюбная помощь – наша визитная карточка – мы на связи, чтобы разрешать ваши вопросы и адаптировать решения под требования вашего бизнеса.
Доверьте вашу потребность в редких металлах профессионалам РедМетСплав и убедитесь в множестве наших преимуществ
Наша продукция:
Труба вольфрамовая ЦСВД Труба вольфрамовая ЦСВД – это высококачественный продукт, предназначенный для использования в различных промышленных и научных отраслях. Благодаря своей высокой прочности и термостойкости, труба обеспечивает надежность в самых экстремальных условиях. Широкий диапазон температур эксплуатации делает её идеальным выбором для работы с высокими нагрузками. Если вы хотите улучшить производственные процессы или исследовательские задачи, вам стоит купить Труба вольфрамовая ЦСВД. Этот материал гарантирует долговечность и эффективность в применении. Не упустите возможность получить лучший продукт на рынке!
loli abounding in vid pic
is.gd/BlCAHo
krtk.rs/e1i0ovy
Мы изготавливаем дипломы психологов, юристов, экономистов и любых других профессий по приятным ценам.– [url=http://ipo.fountain.agri.ruh.ac.lk/employer/land-diplom/]ipo.fountain.agri.ruh.ac.lk/employer/land-diplom[/url]
Купить диплом института по доступной стоимости возможно, обращаясь к проверенной специализированной фирме. Для проверки компании до покупки воспользуйтесь рейтингом и отзывами на форумах. Можно приобрести диплом из любого ВУЗа России [url=http://jaky.com.mx/textstat/kupit-diplom-kolledzha-94/]jaky.com.mx/textstat/kupit-diplom-kolledzha-94[/url]
You’ve made your stand quite nicely!!
canadian casino online https://bhcmerced.org/canadian-casino-online/ best online casino sites canada
Go to our website : http://www.medtronik.ru/
фільми жахів онлайн бойовики та трилери українською в HD
cutty midget girls
fondby.com/SiIu4
onlylinks.cc/gqoU
Для квартиры после затопления сверху натяжной потолок часто спасает отделку и мебель и при этом Перфорация помогает снизить эхо и улучшить разборчивость речи в комнате Если хотите идеальную линию примыкания попросите фотопримеры работ в похожих комнатах в итоге будет аккуратно и практично для ежедневной жизни: https://natyazhnye-potolki-moskva.ru/
Натяжной потолок делает комнату визуально выше и аккуратнее, тканевое полотно и продуманная подсветка меняют восприятие комнаты; перед установкой согласуются светильники, высоты и точки вывода проводов: https://potolki-decarat.ru/
РедМетСплав предлагает широкий ассортимент качественных изделий из ценных материалов. Не важно, какие объемы вам необходимы – от мелких партий до масштабных поставок, мы гарантируем быстрое выполнение вашего заказа.
Каждая единица продукции подтверждена соответствующими документами, подтверждающими их качество. Превосходное обслуживание – то, чем мы гордимся – мы на связи, чтобы ответить на ваши вопросы а также находить ответы под требования вашего бизнеса.
Доверьте потребности вашего бизнеса профессионалам РедМетСплав и убедитесь в широком спектре предлагаемых возможностей
Наши товары:
Поковка висмутовая Sn96,9Bi1,7Cu0,8In0,6 – ISO 9453 Поковка висмутовая Sn96,9Bi1,7Cu0,8In0,6 – ISO 9453 является высококачественным материалом, предназначенным для применения в различных областях, включая электронику и сварку. Этот сплав сочетает в себе идеальные характеристики для обеспечения надежности и долговечности в работе. Благодаря уникальным компонентам, Поковка висмутовая Sn96,9Bi1,7Cu0,8In0,6 – ISO 9453 демонстрирует отличную совместимость с другими материалами, а также устойчивость к коррозии. Не упустите возможность купить Поковка висмутовая Sn96,9Bi1,7Cu0,8In0,6 – ISO 9453 и обеспечить ваш проект качественным сплавом, который значительно повысит его эффективность.
Мы готовы предложить дипломы любых профессий по приятным ценам. Цена будет зависеть от конкретной специальности, года выпуска и образовательного учреждения: [url=http://athena.5nx.ru/viewtopic.php?f=5&t=819/]athena.5nx.ru/viewtopic.php?f=5&t=819[/url]
Продвижение сайтов https://team-black-top.ru под ключ: аудит, стратегия, семантика, техоптимизация, контент и ссылки. Улучшаем позиции в Google/Яндекс, увеличиваем трафик и заявки. Прозрачная отчетность, понятные KPI и работа на результат — от старта до стабильного роста.
Приобрести диплом университета по доступной цене вы сможете, обратившись к проверенной специализированной фирме. Для того, чтобы проверить компанию перед покупкой пользуйтесь рейтингом и отзывами в интернете. Можно заказать диплом из любого университета Российской Федерации [url=http://navyareality.com/author/clay8084295729/]navyareality.com/author/clay8084295729[/url]
Мы изготавливаем дипломы любых профессий по приятным ценам. Диплом об образовании прежде считался ключевым документом, который способствовал быстрому и удачному трудоустройству. Заказать диплом университета!: [url=http://educhoice.co.uk/user/profile/118105/]educhoice.co.uk/user/profile/118105[/url]
Тяговые аккумуляторные https://ab-resurs.ru батареи для складской техники: погрузчики, ричтраки, электротележки, штабелеры. Новые АКБ с гарантией, помощь в подборе, совместимость с популярными моделями, доставка и сервисное сопровождение.
Продажа тяговых АКБ https://faamru.com для складской техники любого типа: вилочные погрузчики, ричтраки, электрические тележки и штабелеры. Качественные аккумуляторные батареи, долгий срок службы, гарантия и профессиональный подбор.
купить диплом медсестры [url=https://www.frei-diplom13.ru]купить диплом медсестры[/url] .
cutty pocket-sized girls
fondby.com/SiIu4
url.sg/JBJX
Good AC care is important for every home. Routine checkups cuts energy bills and increases equipment lifespan.
Продажа тяговых АКБ https://faamru.com для складской техники любого типа: вилочные погрузчики, ричтраки, электрические тележки и штабелеры. Качественные аккумуляторные батареи, долгий срок службы, гарантия и профессиональный подбор.
кіно онлайн вийшли дивитися фільми онлайн безкоштовно
дивитися фільми без реклами мелодрами про кохання онлайн
I’m shocked that this company is still in business. Zero promises, zero results, but they took the money right away. They answer any questions like robots, but no one actually helps. It feels like I’ve fallen for a common [url=https://search-intelligence.co.uk/]SCAM[/url] that just takes money and feeds you empty promises. People, stay away — it’s a complete disappointment!
Кракен Маркетплейс — безопасная площадка для анонимных сделок в 2024 году Kraken darknet **Основной текст (пост на форуме, комментарий, описание):**Для входа используйте только kraken официальная группа.
Explore the latest additions here
Недавно воспользовался печать модели, и получил именно то, что ожидал. Все сделали оперативно, при этом каждая деталь выполнена очень точно. Сотрудники подсказали с подготовкой файла. Цена оказалась доступной, а отзывчивость персонала создали положительное впечатление. Уже планирую новый проект, кто нуждается в услугах 3D-принтера: https://www.fionapremium.com/author/normanmonso/. Наши специалисты выполняют печать точно по макету.
Техническое обслуживание грузовых и коммерческих автомобилей и спецтехники. Снабжение и поставки комплектующих для грузовых автомобилей, легкового коммерческого транспорта на бортовой платформе ВИС lada: https://ukinvest02.ru/
####### OPVA ########
ULTIMATE РТНС COLLECTION
NO PAY, PREMIUM or PAYLINK
DOWNLOAD ALL СР FOR FREE
Description:-> lmy.de/bmRZI
Webcams РТНС since 1999 FULL
STICKAM, Skype, video_mail_ru
Omegle, Vichatter, Interia_pl
BlogTV, Online_ru, murclub_ru
Complete series LS, BD, YWM
Sibirian Mouse, St. Peterburg
Moscow, Liluplanet, Kids Box
Fattman, Falkovideo, Bibigon
Paradise Birds, GoldbergVideo
Fantasia Models, Cat Goddess
Valya and Irisa, Tropical Cuties
Deadpixel, PZ-magazine, BabyJ
Home Made Model (HMM)
Gay рthс collection: Luto
Blue Orchid, PJK, KDV, RBV
Nudism: Naturism in Russia
Helios Natura, Holy Nature
Naturist Freedom, Eurovid
ALL studio collection: from
Acrobatic Nymрhеts to Your
Lоlitаs (more 100 studios)
Collection european, asian,
latin and ebony girls (all
the Internet video) > 4Tb
Rurikon Lоli library 171.4Gb
manga, game, anime, 3D
This and much more here:
or –> cutt.us/OMB2F
or –> citly.me/sVJSf
or –> 4ty.me/08yxs4
or –> tt.vg/fiJTt
or –> tiny.cc/ik3v001
or –> mub.me/qPg
or –> j1d.ca/_I
or –> put2.me/pwdcjb
or –> 74i.de/dekSToh
—————–
—————–
000A000484
слот the dog house Gates of Olympus от Pragmatic Play —
Gates of Olympus — востребованный слот от Pragmatic Play с системой Pay Anywhere, цепочками каскадов и коэффициентами до ?500. Действие происходит у врат Олимпа, где Зевс активирует множители и делает каждый раунд случайным.
Сетка слота представлено в виде 6?5, а комбинация начисляется при появлении от 8 совпадающих символов без привязки к линиям. После выплаты символы удаляются, сверху падают новые элементы, активируя каскады, дающие возможность получить несколько выплат за один спин. Слот является волатильным, поэтому способен долго молчать, но в благоприятные моменты даёт крупные заносы до 5000 ставок.
Чтобы разобраться в слоте доступен демо-версия без вложений. При реальных ставках целесообразно выбирать проверенные казино, например MELBET (18+), учитывая заявленный RTP ~96,5% и правила выбранного казино.
РедМетСплав предлагает широкий ассортимент высококачественных изделий из нестандартных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до масштабных поставок, мы обеспечиваем своевременную реализацию вашего заказа.
Каждая единица продукции подтверждена требуемыми документами, подтверждающими их качество. Дружелюбная помощь – то, чем мы гордимся – мы на связи, чтобы разрешать ваши вопросы а также адаптировать решения под требования вашего бизнеса.
Доверьте вашу потребность в редких металлах специалистам РедМетСплав и убедитесь в множестве наших преимуществ
Наша продукция:
Пруток магниевый ZK60A – WW T-825B Проволока магниевая ZK60A – WW T-825B является высококачественным материалом, предназначенным для различных промышленных и строительных применений. Она отличается отличными механическими свойствами, высокой коррозионной стойкостью и легкостью, что делает её идеальной для использования в авиационной и автомобильной отраслях. Выбор проволоки ZK60A позволяет снизить вес конструкций и увеличить их прочность. Не упустите возможность приобрести этот уникальный продукт! Купить Проволока магниевая ZK60A – WW T-825B можно прямо сейчас, воспользовавшись выгодными условиями.
игра гейтс оф олимпус на деньги
Gates of Olympus slot — известный онлайн-слот от Pragmatic Play с принципом Pay Anywhere, каскадами и коэффициентами до ?500. Игра проходит в мире Олимпа, где верховный бог усиливает выигрыши и превращает каждое вращение динамичным.
Экран игры имеет формат 6?5, а выплата формируется при выпадении не менее 8 совпадающих символов в любой позиции. После выплаты символы удаляются, сверху падают новые элементы, формируя серии каскадных выигрышей, дающие возможность получить серию выигрышей за один спин. Слот считается волатильным, поэтому может долго раскачиваться, но в благоприятные моменты способен порадовать крупными выплатами до 5000 ставок.
Для знакомства с механикой доступен демо-версия без вложений. Для игры на деньги целесообразно рассматривать лицензированные казино, например MELBET (18+), учитывая заявленный RTP ~96,5% и правила выбранного казино.
sonabet com login
Hello!
Is anyone interested in contracting I’m looking to do business with China recently, can anyone tell me if their wedoany.com platform is reliable?
Good luck 🙂
http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4jMsNFN
гражданство румынии
Заказать диплом университета мы поможем. Купить диплом техникума, колледжа в Смоленске – [url=http://diplomybox.com/kupit-diplom-tekhnikuma-kolledzha-v-smolenske/]diplomybox.com/kupit-diplom-tekhnikuma-kolledzha-v-smolenske[/url]
http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4jMsNFN
http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4jMsNFN
sonabet vip
액센트 양벽부 염화칼슘 환안정기금 탈카당 기본조직계 급보 꼬리말 경상 채유탑 https://yak-jiu.com/ – 쪽거울 뒷받침 큰괭이밥 탯바 테스트마케팅 중양화 주훈 관용초 작은갈고리밤나방 라틴방진
The state of Ohio has strict DUI regulations, and understanding their rules is critical if you face charges. A DUI charge is serious and can impact your future.
The blood alcohol concentration threshold in Ohio is eight percent for most drivers and four percent for commercial operators. Officers may administer field or blood and breath tests to verify impairment. Refusing these tests often causes automatic driving privilege loss.
Punishments for DUI offenses in Ohio are based on prior convictions, BAC level, and circumstances. These can include fines, probation, treatment programs, and even imprisonment.
https://rogerbouchardlaw.substack.com/p/ovi-vs-dui-in-ohio-whats-the-legal
[url=https://ao-nutten.de/viewtopic.php?p=54734#p54734]Navigating Pre-Trial Proceedings: Anticipated Steps into Criminal Matters[/url] 0002104
Мы готовы предложить дипломы любой профессии по выгодным ценам. Цена будет зависеть от выбранной специальности, года получения и университета: [url=http://emploi-securite.com/societes/diploman-doku/]emploi-securite.com/societes/diploman-doku[/url]
РедМетСплав предлагает широкий ассортимент отборных изделий из ценных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до масштабных поставок, мы гарантируем оперативное исполнение вашего заказа.
Каждая единица продукции подтверждена требуемыми документами, подтверждающими их происхождение. Дружелюбная помощь – наша визитная карточка – мы на связи, чтобы улаживать ваши вопросы и адаптировать решения под специфику вашего бизнеса.
Доверьте потребности вашего бизнеса специалистам РедМетСплав и убедитесь в множестве наших преимуществ
Наши товары:
Полоса титановая СП 17 Порошок титановый ПТ-7Мсв – ГОСТ 27265-87 – это высококачественный металлопорошок, предназначенный для различных производственных процессов. Он обладает отличными характеристиками, такими как высокая прочность и коррозионная стойкость, что делает его идеальным для применения в авиастроении, машиностроении и других отраслях. Порошок имеет уникальный состав, обеспечивающий отличную адгезию и формуемость. Вы можете купить Порошок титановый ПТ-7Мсв – ГОСТ 27265-87 для повышения качества своей продукции и оптимизации технологических процессов. Не упустите возможность оснастить свое производство проверенным материалом!
Мы можем предложить дипломы любой профессии по приятным ценам. Заказать диплом любого ВУЗа [url=http://daverealestatesurat.com/author/dirk9901593005/]daverealestatesurat.com/author/dirk9901593005[/url]
куплю диплом младшей медсестры [url=https://frei-diplom13.ru]https://frei-diplom13.ru[/url] .
https://sonabet.pro/
cutty loli pint-sized girls
https://is.gd/BlCAHo
гетс оф олимпус
Слот Gates of Olympus — востребованный игровой автомат от Pragmatic Play с механикой Pay Anywhere, каскадными выигрышами и усилителями выигрыша до ?500. Игра проходит на Олимпе, где верховный бог активирует множители и делает каждый раунд непредсказуемым.
Экран игры имеет формат 6?5, а выплата начисляется при выпадении от 8 идентичных символов в любой позиции. После формирования выигрыша символы удаляются, их заменяют новые элементы, формируя серии каскадных выигрышей, дающие возможность получить несколько выплат за одно вращение. Слот считается игрой с высокой волатильностью, поэтому может долго раскачиваться, но при удачных раскладах даёт крупные заносы до 5000 ставок.
Для тестирования игры доступен демо-режим без финансового риска. Для игры на деньги рекомендуется рассматривать проверенные казино, например MELBET (18+), учитывая показатель RTP ~96,5% и правила выбранного казино.
собаки слот казино слот Gates of Olympus —
Gates of Olympus — хитовый онлайн-слот от Pragmatic Play с принципом Pay Anywhere, каскадными выигрышами и множителями до ?500. Игра проходит на Олимпе, где верховный бог повышает выплаты и делает каждый спин случайным.
Сетка слота имеет формат 6?5, а комбинация начисляется при появлении не менее 8 одинаковых символов в любой позиции. После расчёта комбинации символы пропадают, сверху падают новые элементы, формируя каскады, способные принести серию выигрышей за одно вращение. Слот относится игрой с высокой волатильностью, поэтому не всегда даёт выплаты, но в благоприятные моменты даёт крупные заносы до 5000? ставки.
Для тестирования игры доступен бесплатный режим без финансового риска. При реальных ставках рекомендуется выбирать лицензированные казино, например MELBET (18+), ориентируясь на показатель RTP ~96,5% и условия конкретной платформы.
slot gacor situs toto 4d
Практичный площадка купить Автореги Facebook открывает доступ заказать рекламные сущности для таргета. Когда вы планируете купить Facebook-аккаунты, чаще всего важен не «одном логине», а в качестве фарма: уверенный спенд, зеленые плашки в кабинете и правильно созданные ФП. Мы собрали понятную навигацию, чтобы вы без лишних вопросов понимали что подойдет под ваши офферы перед заказом.Коротко: с чего начать: начните с категории Фарм (King), а для серьезных объемов — переходите сразу в разделы под залив: Безлимитные БМ. Важно: аккаунт — это инструмент. Дальше решает подход к запуску: какой прокси используется, как вы передаете лички аккуратно, как проходите чеки и как дублируете кампании. Особенность данной площадки — заключается в наличие приватной базы знаний по FB, где выложены свежие инструкции по проходу ЗРД. Тут можно найти решения Facebook для разных сетапов: от дешевых авторегов и заканчивая мощными Кингами с пройденными запретами. Переходите в наше комьюнити, читайте полезные разборы банов, наводите порядок и повышайте ROI с помощью нашего сервиса прямо сейчас. Дисклеймер: действуйте в рамках закона и всегда в соответствии с правилами Facebook.
http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4jMsNFN
http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4jMsNFN
можно ли купить диплом медсестры [url=http://www.frei-diplom13.ru]можно ли купить диплом медсестры[/url] .
РедМетСплав предлагает широкий ассортимент качественных изделий из ценных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до масштабных поставок, мы гарантируем своевременную реализацию вашего заказа.
Каждая единица изделия подтверждена всеми необходимыми документами, подтверждающими их происхождение. Дружелюбная помощь – наша визитная карточка – мы на связи, чтобы разрешать ваши вопросы по мере того как предоставлять решения под особенности вашего бизнеса.
Доверьте вашу потребность в редких металлах специалистам РедМетСплав и убедитесь в широком спектре предлагаемых возможностей
Наши товары:
Порошок молибденовый МД-8 Порошок молибденовый МД-8 является высококачественным продуктом, используемым в металлургии и промышленности для повышения прочности и коррозионной стойкости. Этот порошок обладает отличными технологическими характеристиками и стабильно высокими показателями чистоты, что делает его идеальным выбором для различных производственных процессов.Применение Порошка молибденового МД-8 обеспечивает надежность деталей и изделий, подвергаемых механическим и термическим воздействиям. Вы можете купить Порошок молибденовый МД-8 прямо сейчас и убедиться в его качестве, который отвечает самым строгим требованиям современных технологий.
폰테크
Южноуральск купить Гашиш
Где купить Бошка Богданович Альфа-ПВП
Альфа-ПВП заказать Грозный
_________________________
Надёжность! Отзывы! Высокое качество!
Проверенный магазин!
____________________________
.
▼▼ ▼▼ ▼▼ ▼▼ ▼▼ ▼▼ ▼▼ ▼▼ ▼▼ ▼▼ ▼▼ ▼▼
[url=https://zinka.cc]✅>> ЖМИ СЮДА <> https://zinka.cc
✅ ЗАХОДИ НА САЙТ! >> zinka.cc
▲▲ ▲▲ ▲▲ ▲▲ ▲▲ ▲▲ ▲▲ ▲▲ ▲▲ ▲▲ ▲▲ ▲▲
ВНИМАНИЕ !!!
! ПРОВЕРЬТЕ ВПН, ЕСЛИ ССЫЛКА НЕ РАБОТАЕТ! !
____________________________
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Конопля
Сленговое название: ‘план’, ‘пастушья сумка’, ‘конопля.
Шишки — это растение травка, как правило используемое в виде смолы (гашиш) или сухой растительной массы. Как правило её употребляют при курении, иногда используют в добавлении в еду. Эффект выражается состоянием расслабленности, повышенным настроением, ощущением «растянутого времени» и обострением вкусовых ощущений, звуковых ощущений и цветового восприятия, часто возникает выраженный аппетит.
При этом план, снижает памятные функции и способность к концентрации, может вызывать чувство тревоги, панические реакции и состояние апатии. Длительное употребление может привести к зависимости, нарушениям с сердечно-сосудистой системой и лёгкими, снижению репродуктивной функции и может вызвать психические расстройства у лиц с склонностью.
[url=https://www.grepmed.com/0q4o2q]Заходи на ZINKA.CC | Гашиш Купить [/url]
[url=http://furniturof.ru/blog/chto-novogo-v-etoj-versii-simply/]САЙТ >>> ZINKA.CC | Метамфетамин ЛИРИКА 200 мг Учалы Купить | САЙТ >>> ZINKA.CC [/url]
[url=https://www.grepmed.com/m8jb20n1]Заходи на ZINKA.CC | Купить План, Синтетический гашиш [/url]
Бутират
Сленговое название: ‘Е’, ‘веселые конфетки’, ‘Ешка’, ‘колеса’, ‘Икс-Ти-Си’ и др.
Восторг — синтетический химия, как правило в виде таблеток, произведённых в незаконных лабораториях. Его эффект — резкий подъём энергии, чувство эйфории, чувственная близость к окружающим и обострённое ощущение звуков и эмоций, поэтому он часто встречается в клубной сцене.
Нежелательные последствия включают перегревание организма, дефицит жидкости, ускоренное сердцебиение и резкий падение настроения после действия. Регулярное употребление может приводить к депрессивным состояниям, перегрузке ЦНС и тяжёлым нарушениям с психическим здоровьем; смертельные случаи чаще обусловлены с гипертермией и сердечными осложнениями.
[url=https://www.grepmed.com/fv1hs8]Где можно купить прегабалин | САЙТ – ZINKA.CC [/url]
[url=https://www.grepmed.com/n43vplse]СОЛЬ Майский купить тест | САЙТ – ZINKA.CC [/url]
[url=https://www.grepmed.com/we8r4tv0]Заходи на ZINKA.CC | можно ли купить Мефедрон [/url]
Опиат
Сленговое название: ‘Гарик’, ‘Герасим’, ‘Хмурый’, ‘Барбадос’, ‘Гера’, ‘Гербалайф’.
Опиоид — тяжёлый морфин, производный от морфиновых соединений, который вводят путём инъекций или курят. Он провоцирует выраженную эйфорию, за которой следует глубокое состояние умиротворения и заторможенности, при этом снижается боль и эмоциональная отзывчивость.
Главная проблема героина — очень сильная зависимость и опасность летальной передозировки. Уличный опиоид часто содержит вредные примеси, а внутривенное употребление ассоциируется с опасностью ВИЧ-инфекции, гепатита и опасных инфекций. Как правило постоянное использование ведёт к физической и психологической аддикции.
[url=http://msegate.mesbahey.com/posts/CzApefHCWI]Заходи на ZINKA.CC | купить Кокс Йошкар-Ола телеграм [/url]
[url=http://refking.ru/]Заходи на ZINKA.CC | Купить Альфа Новокузнецк [/url]
[url=https://www.grepmed.com/gynfn2]Заходи на ZINKA.CC | Купить Камень, АПВП, Стероиды, Пикалёво [/url]
Наркотик
Сленговое название: Кокс, мука, нюхара, кекс, кикер, снег.
Антрацит – мощный стимулятор в виде белого порошкообразного вещества, который чаще всего вдыхают через нос; его разновидность «крэк» курится и оказывает эффект значительно быстрее и интенсивнее. Препарат вызывает кратковременный подъём энергии, уверенности и активности, подавляя чувство голода и ощущение усталости.
По завершении эффекта наступает резкий упадок с тревогой и депрессивным состоянием. Снег разрушает сердце, сосуды и слизистую оболочку носовых ходов, способно вызывать психозы и агрессивное поведение. Выраженная тяга и потеря контроля над использованием в особенности характерны для крэка.
[url=https://www.grepmed.com/cv0pn1uhq]Заходи на ZINKA.CC | MDMA Героин Купить [/url]
[url=https://www.grepmed.com/xm8cu22g4]ZINKA.CC <<>> ZINKA.CC | Лирика Альфа Кристалл Камень A-PVP Купить | САЙТ >>> ZINKA.CC [/url]
[url=http://ventconcept.ru/blog/-ventilyatsiya-i-konditsionirovanie-konditerskoj/#comment_759172]САЙТ >>> ZINKA.CC | Купить Трамадол, План, Анаша | САЙТ >>> ZINKA.CC [/url]
[url=https://thenewdiagrams.com/cgi-bin/guestbook.exe]Заходи на ZINKA.CC | Купить Бошка [/url]
[url=https://www.grepmed.com/peyhl]САЙТ >>> ZINKA.CC | Купить Модафинил | САЙТ >>> ZINKA.CC [/url]
НАРКОТИК
Уличное обозначение: “кислота”.
НАРКОТИК Псилоцибинсодержащие грибные препараты — галлюциногены, способные вызывать сильные изменения сенсорного восприятия, мыслительных процессов и чувства времени. Эффект способно продолжаться от нескольких часов до половины суток и характеризуется интенсивными визуальными и слуховыми искажениями.
Риск заключается в непредвиденности реакции: «негативное путешествие» может спровоцировать панику, психоз или рискованное действия. Не исключены продолжительные психические последствия и неожиданные «эпизоды» галлюцинаторных проявлений даже спустя несколько месяцев после использования.
Мультимедийный интегратор i-tec интеграция мультимедийных систем под ключ для офисов и объектов. Проектирование, поставка, монтаж и настройка аудио-видео, видеостен, LED, переговорных и конференц-залов. Гарантия и сервис.
爱一帆下载海外版，专为华人打造的高清视频平台运用AI智能推荐算法，支持全球加速观看。
Before you start betting, check the betwinner bonus terms at https://bet-promo-codes.com/sportsbook-reviews/betwinner-registration/ to understand how the offer works and how to withdraw your winnings.
гатес оф олимпус
Слот Gates of Olympus — хитовый онлайн-слот от Pragmatic Play с системой Pay Anywhere, цепочками каскадов и усилителями выигрыша до ?500. Игра проходит на Олимпе, где бог грома усиливает выигрыши и превращает каждое вращение случайным.
Игровое поле представлено в виде 6?5, а выплата засчитывается при появлении не менее 8 совпадающих символов без привязки к линиям. После формирования выигрыша символы исчезают, их заменяют новые элементы, активируя серии каскадных выигрышей, дающие возможность получить дополнительные выигрыши за один спин. Слот считается игрой с высокой волатильностью, поэтому не всегда даёт выплаты, но в благоприятные моменты способен порадовать крупными выплатами до 5000 ставок.
Для тестирования игры доступен демо-версия без регистрации. При реальных ставках стоит рассматривать проверенные казино, например MELBET (18+), ориентируясь на показатель RTP ~96,5% и условия площадки.
Мы готовы предложить дипломы любой профессии по приятным тарифам.– [url=http://dentisthome.ir/read-blog/14264_kupit-diplom-o-vysshem.html/]dentisthome.ir/read-blog/14264_kupit-diplom-o-vysshem.html[/url]
Приобрести диплом ВУЗа по выгодной стоимости вы можете, обратившись к проверенной специализированной фирме. Для проверки компании перед покупкой воспользуйтесь реальными отзывами в интернете. Таким образом можно приобрести диплом из любого института России [url=http://cinnamongrouplimited.co.uk/agent/mkalacey67721/]cinnamongrouplimited.co.uk/agent/mkalacey67721[/url]
Посетите официальный сайт бренда : https://neoko.ru/images/pages/promokod_143.html
Мы изготавливаем дипломы психологов, юристов, экономистов и прочих профессий по невысоким тарифам. Стоимость будет зависеть от выбранной специальности, года получения и ВУЗа: [url=http://rsfsr.flybb.ru/viewtopic.php?f=2&t=1020/]rsfsr.flybb.ru/viewtopic.php?f=2&t=1020[/url]
play slots online Gates of Olympus slot —
Gates of Olympus — востребованный онлайн-слот от Pragmatic Play с принципом Pay Anywhere, каскадными выигрышами и множителями до ?500. Сюжет разворачивается на Олимпе, где верховный бог активирует множители и делает каждый раунд динамичным.
Экран игры имеет формат 6?5, а выплата начисляется при выпадении 8 и более одинаковых символов в любом месте экрана. После расчёта комбинации символы исчезают, сверху падают новые элементы, активируя серии каскадных выигрышей, которые могут дать серию выигрышей за один спин. Слот считается высоковолатильным, поэтому может долго раскачиваться, но в благоприятные моменты может принести большие выигрыши до 5000? ставки.
Для тестирования игры доступен демо-режим без вложений. Для ставок на деньги целесообразно выбирать проверенные казино, например MELBET (18+), принимая во внимание заявленный RTP ~96,5% и условия площадки.
Привет, форумчане! Давно сижу в теме Telegram-маркетинга.
Недавно тестировал разные способы рекламы в Telegram, и вот к какому выводу пришел.
Пробовал вручную искать площадки, но это занимает часы, а результат часто разочаровывает.
Поэтому зашел вот в такой обзор — полезно: [url=https://medium.com/@camimoc986/%D0%B1%D0%B8%D1%80%D0%B6%D0%B0-%D1%80%D0%B5%D0%BA%D0%BB%D0%B0%D0%BC%D1%8B-%D0%B2-telegram-%D0%BD%D0%BE%D0%B2%D1%8B%D0%B5-%D0%B2%D0%BE%D0%B7%D0%BC%D0%BE%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D0%B8-%D0%B4%D0%BB%D1%8F-%D0%BF%D1%80%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F-%D0%B2-2026-%D0%B3%D0%BE%D0%B4%D1%83-b3338fafc646]реклама РІ телеграм[/url]
Жду ваших мыслей: как сейчас лучше всего работать с TG-рекламой?
Мы предлагаем дипломы любых профессий по приятным ценам. Приобрести диплом любого ВУЗа [url=http://masterflower.listbb.ru/viewtopic.php?f=6&t=1860/]masterflower.listbb.ru/viewtopic.php?f=6&t=1860[/url]
Visit the brand-new official page : https://jerezlecam.com/
РедМетСплав предлагает обширный выбор качественных изделий из редких материалов. Не важно, какие объемы вам необходимы – от мелких партий до крупных поставок, мы обеспечиваем своевременную реализацию вашего заказа.
Каждая единица товара подтверждена соответствующими документами, подтверждающими их происхождение. Превосходное обслуживание – наш стандарт – мы на связи, чтобы ответить на ваши вопросы по мере того как предоставлять решения под специфику вашего бизнеса.
Доверьте ваш запрос профессионалам РедМетСплав и убедитесь в широком спектре предлагаемых возможностей
поставляемая продукция:
Полоса кобальтовая Stellite 6113 Полоса кобальтовая Stellite 6113 – это высококачественный материал, предназначенный для применения в условиях высокой температуры и износа. Благодаря уникальному составу, эта кобальтовая полоса обладает отличной коррозионной стойкостью и прочностью. Применяется в различных отраслях, включая машиностроение и авиацию. Если вы ищете надежное решение для своих производственных нужд, купить Полоса кобальтовая Stellite 6113 будет отличным выбором. Этот продукт обеспечит долговечность и эффективность в работе, что особенно важно в современных условиях. Не упустите возможность улучшить качество своей продукции, выбрав Полосы кобальтовые.
Современные онлайн казино — это давно не случайные игровые площадки, а полноценная индустрия с понятными правилами и возможностью честного вывода денег. Игроки всё чаще ищут площадки, где можно спокойно играть на деньги, не сомневаясь в честности игр. Именно поэтому мы собрали лучшие онлайн казино на реальные деньги, чтобы вы могли сделать осознанный выбор без потери времени и средств. На первом этапе всегда стоит понимать, на каких условиях вы играете, поэтому мы сразу даём доступ к рейтингу и возможности [url=https://igrati-casino.online/]играть в онлайн казино на деньги[/url] осознанно, а не наугад.
По своей сути онлайн казино представляют собой игровые платформы, где вы создаёте аккаунт, пополняете баланс и играете в слоты, настольные игры или live-казино. Для пользователя главная цель очевидна: безопасность, стабильный вывод выигрыша и понятный интерфейс. Мы учитываем именно эти факторы и постоянно анализируем лучшие казино по наличию лицензии, репутации, срокам вывода и условиям. В обзорах вы найдёте не рекламные обещания, а факты: как работает поддержка, сколько реально ждать вывод и какие суммы доступны для снятия.
Наша команда целенаправленно исключает сомнительные казино и оставляет в рейтинге только казино, которые реально платят от 300 рублей на карту и другие популярные способы оплаты. Мы постоянно актуализируем данные, отслеживаем правки правил и учитываем живые отзывы. Такой подход даёт объективную картину рынка и упрощает поиск надёжного казино без лишних рисков. Все обновляемые рейтинги и честные обзоры вы всегда можете найти на сайте igrati-casino.online — используйте их, чтобы выбрать казино, где выигрыши реально выводятся.
куплю диплом медсестры в москве [url=http://frei-diplom13.ru]куплю диплом медсестры в москве[/url] .
Telechargement officiel de 1xbet telecharger 1xbet apk
Antipublic – Stop Data Exposure Before It Destroys You
Your personal information data breach may already be live on the dark web. Antipublic reveals hidden data exposure risks and protects you from costly security breaches.
Access 33B+ leaked passwords and track 50M new records daily in real time. Scan any user, domain, or email instantly and prevent massive loss before it happens.
Only $2 unlocks full protection.
Check now: [url=https://antipublic.net/referral?code=REF4YIJHD8R] Data breach pdf[/url]
|
中華職棒戰績台灣球迷的首選資訊平台，提供最即時的中華職棒戰績新聞、球員數據分析，以及精準的比賽預測。
Статьи, личный опыт, руководства по преодолению тревоги, развитию критического мышления, гигиене информации и самопомощи.
Корпоративные программы: Психологическая
поддержка сотрудников компаний
для улучшения их благополучия.
Философия: Создание поддерживающего
и человечного пространства, где забота о
ментальном здоровье становится нормой
Тренд на достигаторство я переживаю что в своём возрасте ничего не достиг
В поисках надежного поставщика редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем внушительный выбор продукции, обеспечивая высочайшее качество каждого изделия.
Редметсплав.рф гарантирует все стадии сделки, предоставляя полный пакет необходимых документов для легализации товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы обеспечить любой запрос с прекрасным качеством обслуживания.
Наша команда службы поддержки всегда на связи, чтобы помочь вам в подборе нужных изделий и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете достоверность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что качество и уровень нашего сервиса – идеальный вариант для вас.
Наша продукция:
Медный переходной пресс тройник 40.5х18 мм М3РМ ГОСТ Р 52948-2008 Приобретайте надежные медные переходные тройники для соединения труб с разным диаметром. Устойчивы к коррозии, легки в монтаже и обеспечивают надежное соединение. Широкий выбор размеров. Гарантированное качество и долговечность.
Jeffrey soffer. Nyt connections hints april 6. Nyt connections hints july 26. National parks in california. Online payments. http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4qt76ND
Nflx stock price. Batman begins. Wwe friday night smackdown. Aurora borealis viewing locations monday. Samsung s26 ultra release date. Forbes community support.
Online bank. Best pre training. Golden bachelorette 2024. Who wins love island. The world’s best aquarium. Palmer luckey. Ray ban offer code. Cast of wicked part 2 dorothy. Barcelojna fc. Wealthiest people in america. Verion. World series news. Kpi examples.
Bespoke post new york ny. Stephen covey. Billionaire list. Best vegan protein powder. Sleep sack. http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4qt76ND
Open up a bank account online. Dep la coruna. Highest paid actors. Something worn by an infant or marathon runner. Top women’s pre workout.
Microsoft share. Marvell stock price. Elizabeth warren net worth. Best undress ai. Chinese dollars to us. Vuori discount code. J.j. abrams. What is the best internet. Nasdaq:amd. Best visa card. Richest man on earth. Nottingham forest schedule. Santo tequila. Top rated business schools in us.
Best contact lenses for dry eyes. Self doubt. Kalanithi maran. 90s female singers. Pepe the shrimp. Best electrolyte packets. Longest flight in the world. Velma. http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4qt76ND
Free online computer courses with certificates. Thyssen forbes. Cynthia mans. States. Doktor ganja. News usa.
Best pre workout supplement. Typhlosion lore. Ny times strands. Protein top. Eddie debartolo jr. Fairmont. South park creators net worth. Air max dn. Who won golden bachelorette. Forbes breaking news. American academy trump. Canandaigua ny 14424 united states. Juan carlos escotet. Ai coins.
Dominican peso to usd. Stoic. Nyt connections hints june 12. Dental plan. Best thermometer for newborn. Bachelor 2025 contestants. Goog shares. Dallas mavericks vs lakers. http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4qt76ND
Trump coing. Typical gamer net worth. South park season 28. Math education news. Customer relationship management software. Israel.iran.
Best savings account interest rates. Steve ells. Workday layoffs today. Nintendo switch deals black friday. Дё–з•Њй¦–еЇЊ. Nyt connections hints february 27. Quordle hints. Moon and supermoon. Proctor & gamble layoffs. Net worth of glenn beck. Forbes richest list. Suitcase. Morris chestnut. Best fitness tracker 2024.
Adam sandler. The acolyte. Steve ball.er net worth. When did avicii die. Snow white budget. Forbes strands. http://cl.angel.wwx.tw/debug/frm-s/bit.ly/4qt76ND
Blackfriday 2024. Group 7 meaning. Gold standard whey protein review. Los angles. Safety city in us. Emory university us ranking. Steve huffman.
Cute winter boots meaning. Divorce lawyers near me. Best cat food. Best university in the states. Wiz khalifa age. Todays wordle clue. Who are the richest people in the united states. 3i atlas news. Oscar soccer. Is fiyero the scarecrow. Southpark new season. Scott farmer net worth.
Hello .!
I came across a 152 useful resource that I think you should check out.
This platform is packed with a lot of useful information that you might find valuable.
It has everything you could possibly need, so be sure to give it a visit!
[url=https://www.golinuxhub.com/2021/11/what-is-a-vpn-and-why-you-may-need-one/]https://www.golinuxhub.com/2021/11/what-is-a-vpn-and-why-you-may-need-one/[/url]
Additionally do not neglect, folks, which one at all times are able to inside this article find solutions to address your the very tangled questions. The authors attempted to present all data using the most most easy-to-grasp method.
Промокод 1xBet при регистрации. Компания 1ИксБет заинтересована в поиске новых игроков, поэтому для новых пользователей действует акция в виде приветственного бонуса, который равен сумме первого депозита, но не превышает двести двадцать пять тысяч рублей. Однако при использовании 1xbet new registration promo code букмекерская контора добавит процент к приветственного бонуса. Чтобы получить повышенную сумму на первый депозит, игроку нужно: зайти на сайт букмекера, выбрать создание аккаунта через почту, заполнить данные, ввести промокод и подтвердить согласие с правилами. Акционный код букмекера помогает получить ещё больше бонусов. Такой код представляет собой набор, которая позволяет активировать персональную акцию от букмекера. С его помощью можно получить фрибет и другие подарки.
Musk net worth. Jerry jones. Best protein powder brands. United airlines polaris lounge expansion. Eggs shortage. Pokimane age. Today’s mortgage rates. Stock market donald trump. https://bit.ly/4qt76ND
Did charlie kirk donate money to charities. Tony soprano house. Mstr stock. Billionaires forbes. Refinance mortgage rates. Eric gregg umpire. White house.
Diesel peltz. How a leap of faith might feel nyt. Forbes connections hints. What time does love island come on. Nissan bankruptcies 2024. Sports shocker nyt. Dean and deluca. Lewis howes wikipedia. How many pages should a resume be. Only rock that humans regularly eat. Wireless breast pump. Cosmic brownies ban. Black country artists.
Jersey heights. Largest private companies. My car is a nyt. Eddie van halen. Jeff bezos ex wife. https://bit.ly/4qt76ND
Top charities to donate to. Lucy guo. Shayne coplan. Snow white rating. Tanks. Pesos to dollars. Facebook stock price. Pay per click management.
Nasdaq: ibit. Bill koch. Good first credit card. Angela angela merkel. Drudge report. Most powerful women in the world. Bill chisolm. How to become a motivational speaker. Connections clues today. Ira cd rates. Log in. Don vultaggio. What time is wwe raw tonight.
Мы можем предложить дипломы психологов, юристов, экономистов и других профессий по разумным тарифам. Цена будет зависеть от определенной специальности, года получения и образовательного учреждения: [url=http://biolinkexp.com/teresa28562161/]biolinkexp.com/teresa28562161[/url]
폰테크
Leadership. Nfl 2017 nfl draft. Courtney cox. Ashland university. Great charities to donate to.
Por nhub. The white lotus season 3. John mars. Fred smith. Top ten richest country in world. https://telegra.ph/EHffekt-forera-Sudba-Diskurs-Dejstviya-01-17
Nyse: noc. Rebel stork. Best 0 interest credit cards. When could women get credit cards. Demon slayer kimetsu no yaiba the movie infinity castle. Who is richest man in the world. Ivy league price fixing lawsuit. Shrimp jesus. Employee turnover. What is kpi. Cheers boston. Cadence we were liars.
中華職棒今日比賽結果台灣球迷的首選資訊平台，提供最即時的中華職棒今日比賽結果新聞、球員數據分析，以及精準的比賽預測。
Is there a mcdonald’s in the pentagon. Tiger woods age. Kylian mbappГ©. S&p500 index fund. Black in beauty season 2. Carrie underwood net worth forbes.
Top executive recruiting firms. How can you tell if your phone has been hacked. One day cast. Connection clues today. Kenneth langone. Horizons chapter 2. Tradedesk stock. Shoes for neuropathy. https://telegra.ph/EHffekt-forera-Delo-Test-Lyushera-Frejd-01-17
South park next season. Rich man. Glenn beck net worth. When will interest rates go down. Why is it so hot today. Social capital. Victoria gaetz net worth. Is jurassic world rebirth streaming. Good american family first episode date. Hamste gay. Wordle forbes hint. Chewy promotion codes. Graham hart new zealand. 21st century.
中華職棒今日比賽結果台灣球迷的首選資訊平台，提供最即時的中華職棒今日比賽結果新聞、球員數據分析，以及精準的比賽預測。
сервисы емайл рассылок сервис емейл рассылок россия
сервис smtp рассылки рассылка писем по e mail сервисы
смотреть онлайн смотреть фильмы на телефоне бесплатно
задвижка 30с41нж ду 200 ру 16 задвижка 30с41нж
中華職棒賽程台灣球迷的首選資訊平台，提供最即時的中華職棒賽程新聞、球員數據分析，以及精準的比賽預測。
https://pamyatniki-granitnye.by/
Мы готовы предложить дипломы любой профессии по невысоким тарифам. Быстро купить диплом о высшем образовании [url=http://kingsideaconnections.org/read-blog/3065_kupit-diplom.html/]kingsideaconnections.org/read-blog/3065_kupit-diplom.html[/url]
В поисках надежного поставщика редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем внушительный выбор продукции, обеспечивая высочайшее качество каждого изделия.
Редметсплав.рф защищает все стадии сделки, предоставляя полный пакет необходимых документов для оформления товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы обеспечить любой запрос с непревзойденным обслуживанием.
Наша команда службы поддержки всегда на связи, чтобы помочь вам в подборе нужных изделий и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете достоверность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что качество и уровень нашего сервиса – ваш лучший выбор.
Наша продукция:
Пружина из драгоценных металлов платиновая 50х9х0.5 мм Пл99.9 ТУ Выберите идеальные пружины из золота, серебра или платины, чтобы дополнить ваше украшение. Найдите пружины с изысканным дизайном и прочностью. Они предлагают широкий выбор для того, чтобы подчеркнуть уникальность вашего украшения.
Sketch onlyfans leaks. Don hankey. Cal raleigh contract. Rapids current whirlpool. Richard branson. Smacker mushroom.
Median income by age. Your honor season 3. The last of us season 2. Is weed legal in florida. Xrp stock price. Dogecoin price rally. Red mirage meaning. https://telegra.ph/Den-surka-Kartina-mira-Delo-Parnoyal-01-16
Forbes top 100 richest people. What time does survivor air. Worsle hint. Ashoka season 2. Netfl. Wordle today forbes. December 31. Best fish oil. Madrid cf. Movie the atomic blonde. Luke musgrave injury.
The pitt streaming. Ca state income tax calculator. Tony awards. Chunks of the economy nyt. Social media marketing tips. Louis moore bacon. Does the clocks go back this weekend. Best bed for shoulder pain.
Forbes business. List of united states billionaires. Detroit pistons vs golden state warriors timeline. When is stranger things season five coming out. What crypto to buy now. https://telegra.ph/Holizm-Den-surka-EHffekt-proekcii-YUng-01-16
Price ripple. E. jean carroll. Sport teams. Lloyd blankfein goldman. 50 cent net worth forbes. Where to watch wicked. Connections hint november 13. Pesos to us dollars. Sir ka shing li. Dollar to euro. Cody bellinger contract. Stock price of microsoft. Best renters insurance.
70’s female pop singers. Bellroy. Best children’s smart watch. Eduardo saverin eduardo saverin. Rare beauty net worth.
Abundance mindset after:2020-01-01. Rams vs bills. Movies streaming this weekend. Top 25 influencers in the world. Mayor of kingstown season 4. Best fitness tracker 2024. Everyone watches women’s sports. https://telegra.ph/Holizm-Den-surka-EHffekt-proekcii-YUng-01-16
Forbes top charities 2023 feeding america net assets. U.s. property foreclosures continue increasing. Grant’s women. Largest companies in the world. Doddgers. Coreweave stock news. Richest man in america. Normal us salary. Today’s strands answers. Bruno mars that’s what i. Best heloc rates. The suicide squad.
Hello .!
I came across a 152 helpful site that I think you should dive into.
This site is packed with a lot of useful information that you might find interesting.
It has everything you could possibly need, so be sure to give it a visit!
[url=https://whatsag.com/blog/chic-and-choc-adopt-the-parisian-look.php]https://whatsag.com/blog/chic-and-choc-adopt-the-parisian-look.php[/url]
Furthermore remember not to neglect, everyone, that a person at all times are able to in this article find answers to the the very tangled questions. Our team tried to lay out the complete information via the most extremely accessible method.
best casino online [url=https://magnetgambling.com/online-casinos/]online casinos bonus[/url] best payout online casino real money
How to temporarily disable facebook. Itzhak ezratti wife. Energy transition news today october 2025. Galaxy s25 ultra release date. Yankees net worth. How did elizabeth warren make her money.
Neil.diamond. Dental insurance plans. 45 billion won to usd. Nyt connections hints december 26. Forbes top colleges 2025. The family mcmullen. Today’s refinance rates. Smci earnings. https://telegra.ph/Holizm-Den-surka-EHffekt-proekcii-YUng-01-16
Connections nyt forbes. Connections nyt forbes today. Thomas frist jr. Gme. Canine sunblock. Mat ishbia. Gmail. Best first credit cards. Porn.hub. Top billionaires in the world. Home improvement market news. Taylor swift ring. Michael moritz. Billionaires in usa.
Apple cider vinegar gummies. Jeffrey d morgan. Rajiv jain. Good colleges in usa. Short term medical insurance. Amd stock cost.
Marc rowan. Apple new iphone release date. Golden visa portugal. Kevin ware injury. Best ai undressing. https://telegra.ph/Holizm-Den-surka-EHffekt-proekcii-YUng-01-16
Booz allen hamilton logo. It insists upon itself. Forbes top earning athletes. Automobile insurance. Unitedhealth data breach impact. Connections hint jan 22. Ben roethlisberger. Swedish krona to usd. The philippines. World rich family. Halftime show. Daniel.jones.
РедМетСплав предлагает внушительный каталог качественных изделий из нестандартных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до крупных поставок, мы гарантируем оперативное исполнение вашего заказа.
Каждая единица изделия подтверждена соответствующими документами, подтверждающими их качество. Дружелюбная помощь – наш стандарт – мы на связи, чтобы ответить на ваши вопросы по мере того как предоставлять решения под требования вашего бизнеса.
Доверьте потребности вашего бизнеса профессионалам РедМетСплав и убедитесь в широком спектре предлагаемых возможностей
поставляемая продукция:
Лента магниевая GRE3 Круг магниевый GRE3 – это надежный инструмент для выполнения различных сварочных работ. Изготовленный из высококачественного магния, он гарантирует отличную производительность и долговечность. Этот круг обеспечивает точную обработку, что делает его идеальным выбором для профессионалов и любителей.Его универсальность позволяет использовать круг как для черных, так и для цветных металлов. Если вы хотите купить Круг магниевый GRE3, вы сделаете правильный выбор для повышения эффективности своей работы. Опробуйте этот прочный и легкий инструмент и ощутите разницу в результатах.
Pmp certification. Online universities. Goog after hours. White lotus season 3 episode 6. How many episodes is squid game season 2. New york sinking.
This one and that one nyt. How do you delete a instagram account. Susanne klatten. Overwatch 2 player count. Mgm stock. https://telegra.ph/Holizm-Den-surka-EHffekt-proekcii-YUng-01-16
Aed dirhams to us dollars. Northern lights wisconsin. Ms. frizzle. Alexey mordashov. Who owns discord. Forbes richest. Is prosecco bubbles. Business magazine. Is pbs gone. Forbes travel insurance. Rich men. Apple aapl.
Need an AI generator? undress ai tool The best nude generator with precision and control. Enter a description and get results. Create nude images in just a few clicks.
смотреть онлайн бесплатно кино онлайн
Набрать просмотры в Телеграм бесплатно – ТОП 24 сайта в 2026 году https://vc.ru/2139827
купить диплом медсестры [url=http://www.frei-diplom13.ru]купить диплом медсестры[/url] .
online slots machines слот Gates of Olympus —
Слот Gates of Olympus — популярный онлайн-слот от Pragmatic Play с механикой Pay Anywhere, цепочками каскадов и усилителями выигрыша до ?500. Игра проходит на Олимпе, где верховный бог повышает выплаты и делает каждый раунд случайным.
Игровое поле имеет формат 6?5, а комбинация формируется при выпадении не менее 8 одинаковых символов в любом месте экрана. После расчёта комбинации символы пропадают, их заменяют новые элементы, активируя каскады, способные принести несколько выплат в рамках одного вращения. Слот является высоковолатильным, поэтому способен долго молчать, но при удачных каскадах способен порадовать крупными выплатами до 5000 ставок.
Для знакомства с механикой доступен бесплатный режим без регистрации. Для игры на деньги целесообразно использовать официальные казино, например MELBET (18+), ориентируясь на заявленный RTP ~96,5% и правила выбранного казино.
казино игры онлайн
Слот Gates of Olympus — востребованный игровой автомат от Pragmatic Play с механикой Pay Anywhere, каскадными выигрышами и множителями до ?500. Действие происходит в мире Олимпа, где бог грома активирует множители и превращает каждое вращение непредсказуемым.
Экран игры представлено в виде 6?5, а комбинация формируется при появлении 8 и более совпадающих символов в любой позиции. После формирования выигрыша символы исчезают, сверху падают новые элементы, формируя серии каскадных выигрышей, дающие возможность получить дополнительные выигрыши в рамках одного вращения. Слот относится волатильным, поэтому не всегда даёт выплаты, но при удачных раскладах может принести большие выигрыши до 5000? ставки.
Для знакомства с механикой доступен бесплатный режим без регистрации. При реальных ставках стоит выбирать официальные казино, например MELBET (18+), принимая во внимание показатель RTP ~96,5% и условия площадки.
Why did heidi klum leave agt. How old is jeff bezos. La mussara. Irwin jacobs. Quentin tarantino films.
Voting districts nyt mini. Target boycott 2025. Wordle hints today forbes. Failure quotes. Metlife. https://telegra.ph/Separaciya-EHffekt-prozhektora-CHislo-Donbara-Diskurs-01-18
Korean retinol tea. Charles dickens works. Questioning what kind of development economics we want.. Tony ressler. Sandra ortega mera. Black cards. Forbes 100 cloud companies. Cast of traitors. Summer solstice 2025. Iphone 18 pro max. Wicked movie streaming. Who is rich person.
Brook lopez. America’s richest women. Non wifi baby monitor. Strands answers. Ai music news. Sport teams. Best shampoo for newborn.
Soft rock nyt crossword. Forbes richest people 2025. Computer vision retail news. New streaming movies this weekend. Vince leone. Ryzen 7 9700x. https://telegra.ph/Nevrotik-Narciss-Nejron-Stoicizm-01-18
Mfst stock. Best toddler shoes. Connections hint forbes today. Did jj die in outer banks. Nvidia stock forecast may 2025. Trending jewelry 2025. Applebees. Personal injury lawyer. Artists country. Suing for emotional distress. Gen z marketing. Playing hooky. How tall is cameron brink. Dayforce.
Мы изготавливаем дипломы психологов, юристов, экономистов и прочих профессий по выгодным тарифам.– [url=http://demo.gsewa.org/agent/flynnstandish/]demo.gsewa.org/agent/flynnstandish[/url]
Приобрести диплом института по выгодной цене возможно, обратившись к надежной специализированной компании. Для проверки компании перед покупкой пользуйтесь реальными отзывами на форумах. Можно купить диплом из любого института России [url=http://13.flybb.ru/viewtopic.php?f=20&t=1853/]13.flybb.ru/viewtopic.php?f=20&t=1853[/url]
задвижка ст 30с41нж задвижка стальная 30с41нж
Hi to every one, the contents existing at this site are actually
amazing for people experience, well, keep up the nice work
fellows.
Season reviews, comprehensive summaries of completed campaigns
Сколько действует отношение на перевод в другую часть – контракт на СВО Россия 2026 https://vc.ru/1528277
В поисках надежного поставщика редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем широкий ассортимент продукции, обеспечивая высочайшее качество каждого изделия.
Редметсплав.рф защищает все стадии сделки, предоставляя полный пакет необходимых документов для законного использования товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы поставить любой запрос с прекрасным качеством обслуживания.
Наша команда поддержки всегда на связи, чтобы помочь вам в определении подходящих продуктов и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете надежность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что наше качество и сервис – идеальный вариант для вас.
Наши товары:
Латуное внутреннее стопорное пружинное кольцо 160х3 мм ЛС59-1 ГОСТ 13943-86 Купить латунные внутренние стопорные кольца по ГОСТ от производителя. Надежное крепление и удержание элементов механизмов. Широкий выбор размеров и конфигураций. Высокое качество и надежность. Применение в машиностроении, автомобильной и других отраслях. Обращайтесь к нашим специалистам для получения более подробной информации.
真实的人类第二季高清完整版，海外华人可免费观看最新热播剧集。
Equili
кино онлайн новинки 2025 лучшие франшизы кино смотреть
сервисы емайл рассылок сервисы автоматической рассылки писем на email
Big-bag-rus.ru — биг бэг тара и мягкая тара МКР: прочные биг-бэги для стройматериалов, зерна, гранулята и других сыпучих продуктов. Производство под заказ и со склада, консультация, расчет, доставка по РФ: https://big-bag-rus.ru/
кино онлайн новинки 2025 смотреть дорамы с русской озвучкой
L’offre 1xbet bonus de bienvenue 2026 garantit un bonus jusqu’a 1 750 $ accompagne de 150 tours gratuits sur les jeux de casino, credites directement sur le compte de jeu. Vous pouvez utiliser le bonus immediatement apres le depot, selon les regles de mise precisees par le bookmaker. Une fois la periode de bienvenue terminee, vous pouvez egalement recevoir jusqu’a 30 % de cashback sur les pertes. Toutes les informations sur le 1xbet dernier code promo sont disponibles ici : https://steinberg-dialog.de/wp-content/pgs/le-code-promo-1xbet_bonus.html
the best adult generator pornjourney girlfriend create erotic videos, images, and virtual characters. flexible settings, high quality, instant results, and easy operation right in your browser. the best features for porn generation.
как сделать рассылку сервисы сервисы массовой рассылки email
juegos de apuestas online chile combinadas como funcionan
폰테크
Mail Order Psychedelic
TRIPPY 420 ROOM is presented as a full-service psychedelics dispensary online, with a focus on carefully prepared, high-quality medical products across several product categories.
Before buying psychedelic, cannabis, stimulant, dissociative, or opioid products online, customers are presented with a clear structure including product access, delivery methods, and assistance. The store features more than 200 products covering different formats and preferences.
Shipping costs are calculated according to package size and destination, offering both regular and express delivery options. All orders are backed by a hassle-free returns policy alongside a strong emphasis on privacy and security. Guaranteed stealth delivery worldwide is a core element, without additional charges. All orders are fully guaranteed to ensure uninterrupted delivery.
The product range includes cannabis flowers, magic mushrooms, psychedelic products, opioid medication, disposable vapes, tinctures, pre-rolls, and concentrates. Each item is listed with clear pricing, and visible price ranges for products with multiple options. Additional informational content is included, such as guides like “How to Dissolve LSD Gel Tabs”, and direct access to buy LSD gel tabs and buy psychedelics online.
TRIPPY 420 ROOM operates from the United States, California, and offers multiple communication channels, including phone, WhatsApp, Signal, Telegram, and email support. The service highlights 24/7 express psychedelic delivery, placing focus on accessibility, discretion, and consistent support.
Football match time today, know exactly when games start in your timezone
высокое качество всех представленных деталей https://zapchasti-remont.ru/shop/kolesa2/
У нас в продаже фирменные детали, не китайские аналоги, а оригинальные изделия от известных проверенных производителей
куплю диплом медсестры в москве [url=http://www.frei-diplom13.ru]куплю диплом медсестры в москве[/url] .
Hello lads!
I came across a 153 valuable site that I think you should check out.
This platform is packed with a lot of useful information that you might find interesting.
It has everything you could possibly need, so be sure to give it a visit!
[url=https://www.appletutorials.de/magazin/auswirkungen-von-vpn-auf-die-kryptosicherheit.html]https://www.appletutorials.de/magazin/auswirkungen-von-vpn-auf-die-kryptosicherheit.html[/url]
And don’t overlook, guys, that a person always may within this piece discover answers to address the most tangled queries. The authors made an effort — present all of the data using an most accessible way.
Hello guys!
I came across a 153 useful site that I think you should check out.
This site is packed with a lot of useful information that you might find insightful.
It has everything you could possibly need, so be sure to give it a visit!
[url=https://idealbloghub.com/things-to-do-when-losing-a-football-bet/]https://idealbloghub.com/things-to-do-when-losing-a-football-bet/[/url]
And remember not to neglect, folks, — a person at all times can within this article find answers for your the very complicated inquiries. Our team made an effort to present the complete data using the most accessible way.
Woman singer 70s. 7 little words. Monte carlo hotel las. What is the best teeth whitening. Define chief marketing officer. Fall back 2025.
Colleen hoover books. Mukesh ambani mukesh ambani. Harrison lee van buren. Overly slapdash. Samsung versus lg. Retirement wishes.
Bts 2026 world tour. Sauna blanket. Best cbd for sleep. Czech koruna to usd. Ncis: tony and ziva. Faherty clothing. Bill gates books. Lore marc. Places where weed is legal in europe. Nyt forbes connections. What are the best days to purchase plane tickets. Qmmm stock. Ted turner. Singers 1980s female.
Мы можем предложить дипломы любой профессии по невысоким тарифам.– [url=http://v69-3.flybb.ru/viewtopic.php?f=8&t=1380/]v69-3.flybb.ru/viewtopic.php?f=8&t=1380[/url]
Мы изготавливаем дипломы любой профессии по разумным тарифам. Диплом об окончании университета в СССР считался основным документом, способствовавшим быстрому и успешному поиску работы. Выгодно заказать диплом ВУЗа!: [url=http://gigmambo.co.ke/profile/nelleroldan47/]gigmambo.co.ke/profile/nelleroldan47[/url]
Купить диплом института по выгодной стоимости можно, обращаясь к проверенной специализированной фирме. Для того, чтобы проверить компанию до заказа пользуйтесь отзывами на форумах. В результате можно заказать диплом из любого университета РФ [url=http://little-witch.ru/forum99.html/]little-witch.ru/forum99.html[/url]
Northern lights aurora borealis. Zone of genius. Mike milken. Kombucha. Sheldon adelson. Frank ocean net worth. Mark zuckerberg. Water flosser reviews.
Inter miami. Soprano house. What broadcasters are on nyt. Iphone release. Maggie mcgrath. Watch chi. Star wars: episode ii – attack of the clones.
Gorge soros. White lotus ending. Ending of wicked. World’s top ten richest people. Connections nyt. 1/23/45 and 6/7/89. Guns and moses. Richest country in the world. Best agatha christie novels. Time management. Gannis. Dreka gates net worth forbes.
Do you mind if I quote a few of your posts as long as I
provide credit and sources back to your weblog? My blog site is
in the very same niche as yours and my users would genuinely benefit from some of the information you present here.
Please let me know if this alright with you.
Appreciate it!
600 pounds into dollars. Said gutseriev. Best car shipping companies. Who benefits from dei. Cutting edge technology. Jeff austin tennis. Trump tower las vegas. Alex karp.
Marshall paw patrol: the movie. Unc chapel hill. Widow’s game. The seinfeld episode nyt. Nis to usd. What time is the victoria secret fashion show. Brin google.
Bruno mars that’s what i like. Safra a catz. Female singers eighties. Steve huffman. Nutrisystem reviews. Best new movies. Forbes connections hints. Chancellor of germany angela merkel. 456 billion won to usd. Xrp etf inflows target. Reese witherspoon. Lloyd austin net worth. Uc irvine forbes ranking. Usdt price.
Wordle clue today. Hussain sajwani. Best supplements for weight loss female. Trimmers hair trimmers. Best starter credit card.
Blackfriday 2024. Btc proce. Celebrity billionaires. Highest paid soccer player. Trumps gold toilet. Nyt crossword answers. Commections hints.
Nyt connections hint today. Hotel. I am a surgeon. Forbes 2000. Wwe raw raw results. Scholastic book club promo code. Today’s price of gas. Dod diversity equity inclusion disbandment. Luke nosek. World richest man 2024. Meg whitman. World wealthiest person. Pina and colada. Oil tariffs.
I don’t even know how I ended up here, but I thought this post was good.
I do not know who you are but certainly you are going to a famous blogger if you
are not already 😉 Cheers!
Admiring the commitment you put into your website and
in depth information you offer. It’s great to come
across a blog every once in a while that isn’t the same outdated rehashed material.
Excellent read! I’ve saved your site and I’m adding your RSS feeds
to my Google account.
Weak foot goals, players scoring with non-dominant foot
wonderful put up, very informative. I’m wondering why the other specialists
of this sector don’t realize this. You must continue your writing.
I am sure, you’ve a huge readers’ base already!
What’s up to every body, it’s my first visit of this web site; this weblog consists of amazing and in fact
fine stuff designed for readers.
Доверенность военнослужащего на представление интересов – контракт на СВО Россия 2026 https://vc.ru/1572682
Community Shield livescore, season opener between league and cup champions
爱一番海外版，专为华人打造的高清视频平台，支持全球加速观看。
melbet gratuit pour android melbet apk
casas de Bonos Bienvenida Apuestas online en españa
Мы изготавливаем дипломы любых профессий по разумным тарифам. Цена может зависеть от определенной специальности, года выпуска и образовательного учреждения: [url=http://gitlab.miljotekniska.se/kishaanivitti8/6978826/-/issues/1/]gitlab.miljotekniska.se/kishaanivitti8/6978826/-/issues/1[/url]
silverberg cialis online prescription ramps canada toronto cheap fase cialis https://cialis-otc.com/ – buy cialis online paypal [url=https://cialis-otc.com]cost of cialis 20mg[/url] ńúäúđćŕëč cialis online overnight
site web du casino 1win 1win telecharger
Apuestas EspañA Gana Mundial ganador eurocopa
bookmaker melbet melbet apk
Накрутка лайков в ВК бесплатно: 20 лучших способов – проверенные решения для роста (Решение, которое работает) https://vc.ru/1957114
диплом медсестры с аккредитацией купить [url=www.frei-diplom13.ru/]диплом медсестры с аккредитацией купить[/url] .
Connections hint october 16. Stephen deckoff. Cryptocurrency values. Pierre omidyar. The mandalorian and grogu.
Top 10 universities in usa. Who was the highest paid athlete. Henry meds reviews. Dylan mulvaney. Top ai startups 2025. Top travel destinations 2025. https://telegra.ph/Umnye-citaty-so-smyslom—899-citat-Krasivyj-status—901-citat-01-21
Best vibrator. Mini clues. Ronaldo earn. Forbes 100 companies. Iron fist. The platform. Black & mild. Online side hustles. Is college board a nonprofit. American horror season 5. Driver cooper or butler nyt.
폰테크
C130. Capitani. Do skymiles expire. Dead internet theory. Pepe muppet meme. Pepsi acquires healthier soda brand poppi. Jerry jones net worth. Frontier fiber.
Top companies to work for. Barcelona. Inspirational quotes famous persons. Google owner. Lakers value. Stock wmt. Best work pants. Best zinc supplement. https://telegra.ph/Umnye-mysli—398-citat-Statusy-pro-zhizn-so-smyslom—669-citat-01-21
Ups stock quote. Richest people in america. Your honor season 3. Jan 25 planets align. Protein supplements brands. Customer journey. Tim scott net worth forbes. Top 10 dating websites. Best tom waits songs. Where to stream the substance. Trump wealth.
tuk tuk tug of war
Labubus. Mr beast net worth. Ghost twilight casper. Anton levy. Trump approval rating richest americans. Calculate nyc taxes. Arnold schwarzenegger and chris christie.
Its joever. Nyse: be. Best men’s hair cutting clippers. What is bernie sanders net worth. Ш±Щ…ШІШ§Ш±ШІ. Fact vs opinion. https://telegra.ph/Citaty-pro-zhizn—786-citat-Citata-o-zhizni—688-citat-01-20
Running up that hill lyrics. Forbes woman. Netflix crash. Great american family hulu. Richest black person in america. Best temp agenvies. Top 100 rich person in world. Homophone for a winter vegetable. Nyt connections hints april 19. Who does joan end up with. World series. Apple ios updates news. How many grammys does kendrick lamar have.
Standard normal plain nyt. Glp-1 weight loss. Shekel to usd. Iphone 18. Crm share. Wealthiest woman in the us. Dei rollback list.
Adsk stock. Highest paid athlete. Approval rating trump. Pi network news. Ariana grande 2020. Toyota celica 2025. Vivek ramaswamy net worth. Harry potter movies list in order 1-8. https://telegra.ph/Frazy-kotorye-zastavlyayut-zadumatsya-o-zhizni—248-citat-Status-so-smyslom—641-citat-01-21
Spring equinox 2025. Seagate company. Forbes billionaire list. Top rated waterpik. Forbes best credit cards. Paul newman rolex daytona. Shari redstone. Tanishq. Someone great. Jared isaacman harbortouch. Prescription drug plans. Univ of mich ann arbor. Planets align 2025. Executive headhunters.
В поисках надежного поставщика редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем широкий ассортимент продукции, обеспечивая превосходное качество каждого изделия.
Редметсплав.рф гарантирует все стадии сделки, предоставляя полный пакет необходимых документов для законного использования товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы обеспечить любой запрос с прекрасным качеством обслуживания.
Наша команда поддержки всегда на связи, чтобы помочь вам в определении подходящих продуктов и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете надежность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что наше качество и сервис – наилучшее решение для вашего бизнеса.
Наша продукция:
Инструментальная круглая поковка 145 мм Х12МФ ГОСТ 1133-71 Широкий выбор круглых поковок для профессиональной обработки металла. Инструментальная круглая поковка высочайшего качества с разнообразием размеров и форм. Повышенная прочность, износостойкость и превосходное качество изготовления. Обеспечивает отличное сцепление с материалом и эффективную работу оборудования. Покупайте прямо сейчас!
telecharger l’application 1win 1win apk
где найти промокод для 1xBet Активируйте бонусом при регистрации на http://modost.ru/wp-content/pages/kakie_diski_ispolyzuyutsya_na_mersedes.html и получите 32 500? + бонус 100%, чтобы начать игру.
Приобрести диплом университета по невысокой стоимости возможно, обращаясь к проверенной специализированной фирме. Для проверки компании перед покупкой воспользуйтесь реальными отзывами в сети интернет. Можно заказать диплом из любого института Российской Федерации [url=http://tripta.social/read-blog/45438_kupit-diplom-kolledzha.html/]tripta.social/read-blog/45438_kupit-diplom-kolledzha.html[/url]
TUK TUK RACING KENYA
Round 5 kicks off — and the race went to another level.
This is TUK-TUK RACING KENYA, where raw skill meets street instincts.
In this round, drivers face a brutal new round:
• sharp corners mixed with water traps
• visual chaos and surprise obstacles
• envelopes with cash on the line
• and a no-mercy TUK-TUK TUG OF WAR finale — where strength beats speed
The action explodes, rankings shift constantly, and everyone is at risk till the last moment.
One mistake and you’re out. One solid move takes you forward.
This is not scripted.
You can’t predict what happens next.
This is Kenya’s Tuk-Tuk Showdown — Round 5.
Watch till the end and tell us:
Which driver stood out the most?
Привет, уважаемые форумчане!
Мы рады вам представить площадку BlackSprut.
https://blacksprut.work
bs2best, bs2site2, black sprut com bs2web top, black sprut blacksprute com, black sprut torrent magnet
цена кв м квартиры жк светский лес застройщик
РедМетСплав предлагает обширный выбор качественных изделий из ценных материалов. Не важно, какие объемы вам необходимы – от мелких партий до крупных поставок, мы гарантируем быстрое выполнение вашего заказа.
Каждая единица товара подтверждена соответствующими документами, подтверждающими их соответствие стандартам. Превосходное обслуживание – наш стандарт – мы на связи, чтобы разрешать ваши вопросы по мере того как находить ответы под требования вашего бизнеса.
Доверьте вашу потребность в редких металлах профессионалам РедМетСплав и убедитесь в гибкости нашего предложения
Наша продукция:
Полоса магниевая A5.24 (ERZr3) – AWS A5.24 Порошок магниевый A5.24 (ERZr2) – AWS A5.24 является высококачественным материалом, предназначенным для сварки и других металлургических процессов. Он обеспечивает отличные механические свойства и коррозионную стойкость. Этот порошок широко используется в аэрокосмической и автомобильной промышленности, где требуются надежные и прочные соединения. Купить Порошок магниевый A5.24 (ERZr2) – AWS A5.24 – значит инвестировать в качество и долговечность ваших изделий. Выберите профессиональный подход к сварочным работам и обеспечьте себе идеальные результаты!
Хроническая усталость — признак чужого пути.
https://dzen.ru/a/aXHyZKIqwmcfjrhy
-генератор по дизайну человека;
-тип личности генератор;
-тип генератор в дизайне человека;
-хьюман дизайн генератор;
-генератор тип личности дизайн человека;
Устали заставлять себя работать силой? Включите сакральный поток и не работайте больше не дня.
https://bit.ly/generator-human-design-live
-тип личности генератор это;
-тип генератор в дизайне человека;
-генератор по дизайну человека;
-тип личности генератор дизайн;
-генератор это в дизайне человека;
Выгорание — это плата за неверность себе. Верните драйв через понимание механики.
https://generator-human-design-tut.g-u.su
-генераторы дизайн человека;
-генератор это в дизайне человека;
-тип личности генератор дизайн;
-хьюман дизайн генератор;
-тип личности генератор дизайн человека;
-тип генератор в дизайне человека;
-генератор в хьюман дизайне;
Hello .!
I came across a 153 useful site that I think you should visit.
This platform is packed with a lot of useful information that you might find interesting.
It has everything you could possibly need, so be sure to give it a visit!
[url=https://thehomeinfo.com/how-to-log-in-to-your-22bet-account-offers/]https://thehomeinfo.com/how-to-log-in-to-your-22bet-account-offers/[/url]
Furthermore do not forget, guys, which you always may within the publication discover answers for the most the absolute tangled inquiries. The authors made an effort — explain all of the content using the extremely accessible method.
la mejor pagina de apuestas deportivas
Check out my blog Basketball-Wetten.Com
Опять приняли решение из головы? База дизайна человека вернет точность выбора.
https://generator-human-design-tut.g-u.su
-дизайн человека генератор описание;
-генераторы дизайн человека;
-генератор тип личности;
-генератор в хьюман дизайне;
-человек генератор дизайн человека;
-человек генератор кто это;
-генератор тип личности дизайн человека;
Сливаете энергию на чужие цели? Найдите свой истинный отклик.
https://generator-human-design-tut.g-u.su
-тип личности генератор дизайн;
-тип личности генератор;
-тип личности генератор это;
-генератор по дизайну человека;
-генератор это в дизайне человека;
-генератор тип личности;
-человек генератор кто это;
Устали заставлять себя работать силой? Включите сакральный поток и не работайте больше не дня.
https://generator-human-design-tut.g-u.su
-тип личности генератор;
-тип личности генератор это;
-дизайн человека генератор;
-генератор тип личности;
-генератор в хьюман дизайне;
ТОП 25 лучших способов для продвижения в Инстаграм в 2026 году (раскрываю все секреты) https://vc.ru/1667626
Хроническая усталость — признак чужого пути.
https://generator-human-design-tut.g-u.su
-человек генератор дизайн человека;
-тип личности генератор это;
-генератор это в дизайне человека;
-тип личности генератор;
-дизайн человека генератор описание;
-генератор тип личности дизайн;
-генераторы дизайн человека;
Вы сгораете, пока другие богатеют. Ваша жизнь — ресурс в чужих руках. Вы — массовка в собственном сценарии.
https://dzen.ru/a/aXHyZKIqwmcfjrhy
-человек генератор дизайн человека;
-генераторы дизайн человека;
-тип личности генератор;
-генератор тип личности дизайн;
-хьюман дизайн генератор;
-генератор тип личности дизайн человека;
Устали заставлять себя работать силой? Включите сакральный поток и не работайте больше не дня.
https://generator-human-design-tut.g-u.su
-генератор это дизайн человека;
-дизайн человека генератор;
-тип личности генератор это;
-генератор по дизайну человека;
-тип личности генератор дизайн;
폰테크
Мы готовы предложить дипломы психологов, юристов, экономистов и прочих профессий по приятным ценам. Купить диплом ВУЗа [url=http://paning.flybb.ru/viewtopic.php?f=7&t=2165/]paning.flybb.ru/viewtopic.php?f=7&t=2165[/url]
Мы изготавливаем дипломы любых профессий по приятным ценам. Диплом об образовании ранее считался ключевым документом, способствовавшим быстрому и удачному устройству на работу. Заказать диплом о высшем образовании!: [url=http://empleosrapidos.com/companies/originality-diplomiki/]empleosrapidos.com/companies/originality-diplomiki[/url]
Ваш бизнес — болото из «надо»? Стройте успех только на своем «Да».
https://generator-human-design-tut.g-u.su
-генератор это дизайн человека;
-тип личности генератор дизайн;
-дизайн человека генератор кто это;
-человек генератор кто это;
-генератор по дизайну человека;
-тип личности генератор это;
Хватит инвестировать свой ресурс в мусор. Ваш мотор заведен для чужой поездки.
https://dzen.ru/a/aXHyZKIqwmcfjrhy
-генератор по дизайну человека;
-тип личности генератор дизайн;
-человек генератор кто это;
-дизайн человека генератор кто это;
-генератор тип личности дизайн человека;
-хьюман дизайн генератор;
Нужен проектор? projector24.ru/ большой выбор моделей для дома, офиса и бизнеса. Проекторы для кино, презентаций и обучения, официальная гарантия, консультации специалистов, гарантия качества и удобные условия покупки.
Хватит предавать себя ради чужого одобрения. Отдаете всё другим, оставляя себе пустоту.
https://bit.ly/generator-human-design-live
-тип личности генератор дизайн;
-генератор в хьюман дизайне;
-генератор тип личности;
-генераторы дизайн человека;
-тип личности генератор;
Мы изготавливаем дипломы любой профессии по приятным ценам.– [url=http://proyectobienes.net/estate_agent/heikeinglis382/]proyectobienes.net/estate_agent/heikeinglis382[/url]
Здравствуйте! Хочу поделиться находкой. Недавно нашел рабочий маркетплейс, все проверил лично.
[b]Мой отзыв:[/b]
Покупал недавно, все норм. Заказ обработали быстро, доставка в срок. Качество товара соответствует описанию. Никаких нареканий нет, все честно и прозрачно.
[b]Почему рекомендую:[/b]
100% наход для тех, кто ценит надежность. Квест изи – все интуитивно понятно. Ссылка рабочая, проверял несколько раз. Площадка стабильная, проблем не было.
Рабочая ссылка: [url=https://mgmarket6.blog]mgmarket6 at[/url]
Использую уже несколько месяцев, все отлично работает. Если нужна проверенная площадка – рекомендую.
[i]mgmarket, mgmarket 6at, mgmarket 5at, mgmarket 6 at, mgmarket 5 at, mgmarket 7at , mgmarket 8at, mgmarket 7 at, https mgmarket, mgmarket at, mgmarket 4at, meга сила рабочая mgmarket 5 at, почему не работает mgmarket[/i]
Wondering how to register betwinner or how to create betwinner account? You’ll find all details and screenshots on https://bet-promo-codes.com/sportsbook-reviews/betwinner-registration/.
Мы изготавливаем дипломы любых профессий по выгодным ценам. Цена может зависеть от выбранной специальности, года получения и ВУЗа: [url=http://blackgulf.com/diplom-za-korotkij-srok-sroki-ceny-uslovija-475-2/]blackgulf.com/diplom-za-korotkij-srok-sroki-ceny-uslovija-475-2[/url]
Hello guys!
I came across a 153 awesome page that I think you should browse.
This resource is packed with a lot of useful information that you might find valuable.
It has everything you could possibly need, so be sure to give it a visit!
[url=https://ideasforeurope.com/does-22bet-have-a-welcome-bonus/]https://ideasforeurope.com/does-22bet-have-a-welcome-bonus/[/url]
Furthermore remember not to neglect, folks, that a person at all times may inside the piece locate answers to the most the very confusing questions. We attempted to explain the complete content using an extremely understandable way.
Кредит наличными в Казахстане подходит для повседневных нужд. Деньги выдаются без целевого назначения. Онлайн заявка ускоряет процесс. Условия зависят от выбранного предложения. Такой кредит легко оформить: spisok-kreditov.ru
oddset die sportwetten tipps
My web site … handicap wetten strategie
Visit the fresh platform > https://panamar.ru/mt/?1xbet_promokod_bonus__4.html
Хроническая усталость — признак чужого пути.
http://8ua.ru/EhN0eUQt/
-человек генератор дизайн человека;
-генератор по дизайну человека;
-человек генератор кто это;
-генератор в хьюман дизайне;
-тип генератор в дизайне человека;
Ваш бизнес — болото из «надо»? Стройте успех только на своем «Да».
http://8ua.ru/9zc8BkNd/
-генератор в хьюман дизайне;
-тип генератор в дизайне человека;
-дизайн человека генератор;
-тип личности генератор дизайн человека;
-генератор тип личности;
-человек генератор дизайн человека;
-генератор это дизайн человека;
como funcionan los stakes en impuestos Apuestas Deportivas
beste sportwetten
My web-site: tipico basketball Wetten
buchmacher pferderennen
Also visit my web site: Neueste Wettanbieter
Honda electric vehicles focus on reliability, comfort, and user-friendly design. The brand is expanding its EV lineup with global models aimed at mainstream buyers https://ev.motorwatt.com/ev-database/database-electric-cars/
pferderennen wetten quoten
Here is my webpage: Alle Wettanbieter Im Vergleich
Купить попперсы в Санкт-Петербурге и Москве https://poppers51.ru/ по выгодной цене
быстрая доставка попперсов в день заказа высокое качество от производителя
Вакансии военной службы по контракту в России на 2026 год для участия в СВО https://vc.ru/1413281
В поисках надежного поставщика редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем внушительный выбор продукции, обеспечивая превосходное качество каждого изделия.
Редметсплав.рф защищает все стадии сделки, предоставляя полный пакет необходимых документов для легализации товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы выполнить любой запрос с прекрасным качеством обслуживания.
Наша команда поддержки всегда на связи, чтобы помочь вам в определении подходящих продуктов и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете уверенность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что наше качество и сервис – ваш лучший выбор.
поставляемая продукция:
Дюралевая прямоугольная труба 80х40х3х5000 мм Д16Т ТУ Познакомьтесь с высококачественными дюралевыми прямоугольными трубами на сайте компании Редметсплав.рф. Прочные, легкие, устойчивые к коррозии и универсальные – идеальный выбор для создания различных конструкций. Убедитесь сами в многообразии применения и преимуществах!
лучшая химчистка обуви отдать обувь в химчистку
покупка квартиры жк светский лес сочи
сколько стоит квартира жк светский лес сочи цены
квартиры от застройщика купить квартиру жк светский лес
химчистка сдать обувь химчистка кожаной обуви
Где в вашем графике ваша жизнь? Чужие «хочу» задушили ваше «люблю».
http://8ua.ru/fwugchyE/
-дизайн человека генератор кто это;
-хьюман дизайн генератор;
-тип генератор в дизайне человека;
-тип личности генератор;
-генератор в хьюман дизайне;
Зайди на официальный сайт компании > http://hammill.ru/
РедМетСплав предлагает широкий ассортимент качественных изделий из редких материалов. Не важно, какие объемы вам необходимы – от небольших закупок до масштабных поставок, мы гарантируем быстрое выполнение вашего заказа.
Каждая единица продукции подтверждена соответствующими документами, подтверждающими их качество. Опытная поддержка – наша визитная карточка – мы на связи, чтобы улаживать ваши вопросы и находить ответы под требования вашего бизнеса.
Доверьте потребности вашего бизнеса профессионалам РедМетСплав и убедитесь в широком спектре предлагаемых возможностей
Наши товары:
Круг танталовый Т-4 Круг танталовый Т-4 – это высококачественный продукт, который используется в различных отраслях, включая электронику и химию. Этот круг обладает отличной коррозионной стойкостью и высокой прочностью. Он идеален для применения в агрессивных средах. Благодаря уникальным свойствам тантала, круг обеспечит надежность и долговечность ваших изделий. Если вы ищете надежный материал для своих проектов, купить Круг танталовый Т-4 – это правильное решение. Выберите качество и уверенность в каждом проекте с нашим продуктом.
Buy LSD Gel Tabs
TRIPPY 420 ROOM operates as a dedicated online psychedelics dispensary, focused on offering carefully crafted and top-quality medical products across several product categories.
Before purchasing psychedelic, cannabis, stimulant, dissociative, or opioid products online, buyers are given a transparent framework including product access, delivery methods, and assistance. The platform lists over 200 products in various formats.
Shipping is quoted based on package size and destination, and includes both regular and express shipping. Orders are supported by a hassle-free returns process and a strong focus on privacy and security. The service highlights guaranteed worldwide stealth delivery, with no added fees. All orders are fully guaranteed to maintain consistent delivery.
The catalog spans cannabis flowers, magic mushrooms, psychedelic products, opioid medications, disposable vapes, tinctures, pre-rolls, and concentrates. All products are shown with transparent pricing, and visible price ranges for products with multiple options. Educational material is also provided, such as guides like “How to Dissolve LSD Gel Tabs”, along with direct options to buy LSD gel tabs and buy psychedelics online.
TRIPPY 420 ROOM operates from the United States, California, while maintaining several contact options, such as phone, WhatsApp, Signal, Telegram, and email. The platform promotes round-the-clock express psychedelic delivery, framing the service around accessibility, privacy, and ongoing customer support.
Устали заставлять себя работать силой? Включите сакральный поток и не работайте больше не дня.
https://telegra.ph/Dizajn-cheloveka-raschet-Human-design-chto-ehto-Kto-takoj-manifestor-Proektor-dizajn-cheloveka-01-24
-тип личности генератор это;
-тип генератор в дизайне человека;
-генератор это в дизайне человека;
-генератор это дизайн человека;
-человек генератор кто это;
-генераторы дизайн человека;
Где в вашем графике ваша жизнь? Чужие «хочу» задушили ваше «люблю».
https://telegra.ph/Gennye-klyuchi-rasschitat-Rasschitat-dizajn-cheloveka-onlajn-Profil-cheloveka-ehto-Profil-cheloveka-ehto-01-24
-тип личности генератор;
-дизайн человека генератор кто это;
-тип личности генератор дизайн человека;
-человек генератор кто это;
-тип личности генератор это;
-генератор тип личности дизайн человека;
Устали заставлять себя работать силой? Включите сакральный поток и не работайте больше не дня.
https://telegra.ph/Dizajn-chelovek-Profil-cheloveka-ehto-Dizajn-cheloveka-raschet-karty-Dizajn-chelovek-onlajn-01-24
-дизайн человека генератор;
-хьюман дизайн генератор;
-тип личности генератор;
-генераторы дизайн человека;
-генератор тип личности;
Также возможен заказ детали практически на все марки стиральных машин официально представленные в России как оптовыми партиями так и в единичном экземпляре https://zapchasti-remont.ru/shop/detali_bloka_tsilindrov/
Ваш бизнес — болото из «надо»? Стройте успех только на своем «Да».
https://telegra.ph/Dizajn-cheloveka-sovmestimost-Bodigraf-cheloveka-Sakralnyj-generator-Dizajn-cheloveka-chto-ehto-takoe-01-24
-генератор тип личности дизайн человека;
-генератор это дизайн человека;
-генераторы дизайн человека;
-генератор тип личности;
-тип генератор в дизайне человека;
Выгорание — это плата за неверность себе. Верните драйв через понимание механики.
https://telegra.ph/Profil-cheloveka-ehto-Raschet-bodigrafa-Svoj-dizajn-Rasschitat-dizajn-cheloveka-po-date-rozhdeniya-01-24
-тип личности генератор это;
-тип генератор в дизайне человека;
-генератор это дизайн человека;
-тип личности генератор дизайн человека;
-генератор это в дизайне человека;
-дизайн человека генератор кто это;
Накрутка лайков ВК – 25 способов накрутки в 2026 году
Подробная информация доступна для просмотра – https://vc.ru/1611355
Ваш бизнес — болото из «надо»? Стройте успех только на своем «Да».
https://telegra.ph/Arhetipy-po-date-rozhdeniya-Manifestor-Human-dizain-Human-design-space-01-24
-тип личности генератор;
-тип личности генератор дизайн;
-хьюман дизайн генератор;
-генераторы дизайн человека;
-генератор по дизайну человека;
-дизайн человека генератор описание;
-тип генератор в дизайне человека;
Выгорание — это плата за неверность себе. Верните драйв через понимание механики.
https://telegra.ph/Sovmestimost-po-dizajnu-cheloveka-Bodigraf-onlajn-Hyuman-dizajn-tipy-lichnosti-Dizajn-cheloveka-onlajn-raschet-01-24
-дизайн человека генератор;
-дизайн человека генератор кто это;
-тип личности генератор;
-человек генератор дизайн человека;
-генератор тип личности дизайн человека;
-человек генератор кто это;
-генератор тип личности дизайн;
Всем привет. Хочу поделиться проверенной площадкой, которой сам пользуюсь.
Мой опыт:
Недавно оформлял заказ — всё прошло без проблем. Обработка быстрая, доставка в срок, товар полностью соответствует описанию. Никаких сюрпризов, всё честно.
Почему могу рекомендовать:
Площадка стабильная и понятная, интерфейс простой, разобраться легко. Ссылка рабочая, проверял неоднократно. За несколько месяцев использования проблем не возникало.
Ссылка на маркетплейс:
[url=https://mgmarket6.dev]mgmarket6 at[/url]
Если ищете надёжный вариант и не хотите рисковать — можно смело рассмотреть.
[i]mgmarket, mgmarket 6at, mgmarket 5at, mgmarket 6 at, mgmarket 5 at, mgmarket 7at, mgmarket 8at, mgmarket 7 at, https mgmarket, mgmarket at6, mgmarket 4at, meга сила рабочая mgmarket 5 at, почему не работает mgmarket, mgmarket4 at, mgmarket5 at, https mgmarket5 at, http mgmarket5 at, mgmarket5 ay, https mgmarket5 at main, https mgmarket5 at login html, http mgmarket5 at скачать, mgmarket5 at l, mgmarket6 at, https mgmarket6 at, http mgmarket6 at, mgmarket6 at не работает, https mgmarket6 at main, https mgmarket6 at login html, https mgmarket6 at captcha, mgmarket6 at host error, mgmarket6 co, mgmarket6 ay, https mgmarket6 at captcha 178775 index, mgmarket6 t 5, mgmarket6 at [/i]
промокод 1xbet бесплатно Найдите промокод на https://thaistore.ru/catalog/pgs/promokod_252.html и активируйте бонус 100% на первый депозит, чтобы начать игру.
У вас есть проблемы со спамом на этом блоге? Я тоже веду блог и хотел бы узнать, как у вас с этим. У нас есть хорошие методы — можем обменяться решениями. Напишите, если интересно.
https://solinfoperu.net/pinco-casino-realnye-promokody-demo-sloty-bez-4/
Потеряли годы на ненужные проекты? Расчет покажет ваш путь.
https://telegra.ph/Dizajn-cheloveka-obuchenie-Manifestor-dizajn-cheloveka-Dizajn-cheloveka-chto-ehto-takoe-prostymi-slovami-Dizajn-cheloveka-rasshi-01-24
-тип личности генератор дизайн человека;
-человек генератор кто это;
-генератор тип личности;
-генераторы дизайн человека;
-хьюман дизайн генератор;
Тело болит от чужих задач? Выжаты как лимон ради чужих идей. Вы — батарейка для чужих амбиций.
https://telegra.ph/Sakralnyj-generator-Raschet-karty-dizajn-cheloveka-Arhetipy-po-date-rozhdeniya-Ra-uru-hu-01-24
-генератор тип личности дизайн;
-дизайн человека генератор описание;
-человек генератор кто это;
-человек генератор дизайн человека;
-тип личности генератор это;
Опять приняли решение из головы? База дизайна человека вернет точность выбора.
https://telegra.ph/Dizajn-cheloveka-onlajn-Dizajn-cheloveka-raschet-Dizajn-cheloveka-manifestor-Arhetipy-po-date-rozhdeniya-01-24
-генератор тип личности дизайн;
-тип генератор в дизайне человека;
-человек генератор кто это;
-дизайн человека генератор описание;
-дизайн человека генератор кто это;
-человек генератор дизайн человека;
Где в вашем графике ваша жизнь? Чужие «хочу» задушили ваше «люблю».
https://telegra.ph/CHto-takoe-dch-Hyumen-dizajn-Gennye-klyuchi-rasshifrovka-Postroit-bodigraf-01-24
-генератор по дизайну человека;
-генератор в хьюман дизайне;
-дизайн человека генератор описание;
-дизайн человека генератор кто это;
-тип личности генератор;
-человек генератор дизайн человека;
Хватит предавать себя ради чужого одобрения. Отдаете всё другим, оставляя себе пустоту.
https://telegra.ph/Hyuman-dizajn-rasschitat-Proektor-dizajn-cheloveka-CHto-takoe-dizajn-cheloveka-Manifestor-01-24
-генератор тип личности;
-человек генератор дизайн человека;
-тип генератор в дизайне человека;
-человек генератор кто это;
-генератор по дизайну человека;
-дизайн человека генератор описание;
проектор на стену интернет-магазин проекторов
Howdy! [url=https://tajmeds.top/#]us pharmacy online[/url] beneficial site.
7k casino позволяет играть в слоты в онлайн формате без установки программ. Достаточно открыть сайт в браузере. Игры корректно работают на разных устройствах. Производительность остается стабильной. Это удобно для повседневного использования: 7k casino вход
Рейтинг 25 лучших сервисов для накрутки подписчиков в Телеграм бесплатно (обновлено 04.06.2026) https://vc.ru/1492114
В поисках достоверного источника редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем широкий ассортимент продукции, обеспечивая превосходное качество каждого изделия.
Редметсплав.рф защищает все стадии сделки, предоставляя полный пакет необходимых документов для законного использования товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы поставить любой запрос с непревзойденным обслуживанием.
Наша команда службы поддержки всегда на связи, чтобы помочь вам в подборе нужных изделий и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете достоверность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что наше качество и сервис – ваш лучший выбор.
Наша продукция:
Медный литой тройник 46.2х1.8 мм с ВР цилиндрической резьбой под пайку G 1 1/4 13.5 мм М2р ГОСТ Р 52949-2008 Покупайте медный литой тройник 46.2х1.8 мм с ВР цилиндрической резьбой под пайку G 1 1/4 13.5 мм на Редметсплав.рф. Идеальное решение для соединения труб в системах водоснабжения и отопления. Высокое качество, надежность и легкость монтажа. Долговечное соединение и безопасность работы системы.
bresanibruno crowing monograph gencligin bookmobile navait degradation undertrykt nieszcz relict https://canadapharmacy-usa.net/drug/besivance-ophthalmic-solution/ – surveys unverifiable alokasi gabka historique radioocarbon regensburg nasz blatt plastics
Вы сгораете, пока другие богатеют. Ваша жизнь — ресурс в чужих руках. Вы — массовка в собственном сценарии.
https://telegra.ph/Dizajn-lichnosti-Dizajn-cheloveka-raschet-karty-Dizajn-chelovek-Dizajn-cheloveka-bodigraf-01-24-2
-генераторы дизайн человека;
-хьюман дизайн генератор;
-дизайн человека генератор кто это;
-генератор по дизайну человека;
-человек генератор кто это;
-генератор это дизайн человека;
-генератор тип личности дизайн человека;
pferderennen mannheim wetten
Look into my blog post sportwetten bonus Mit paypal
Выгорание — это плата за неверность себе. Верните драйв через понимание механики.
https://telegra.ph/Hyuman-dizajn-Tip-lyudej-Manifestor-ehto-Dizajn-chelovek-01-24
-генератор это дизайн человека;
-тип личности генератор дизайн;
-человек генератор кто это;
-дизайн человека генератор;
-генератор в хьюман дизайне;
-дизайн человека генератор кто это;
-генератор это в дизайне человека;
Как раскрутить Instagram – Мои находки 2026 года (ТОП-20 сайтов)
Узнать подробнее https://vc.ru/2616716
РедМетСплав предлагает обширный выбор высококачественных изделий из редких материалов. Не важно, какие объемы вам необходимы – от мелких партий до обширных поставок, мы гарантируем своевременную реализацию вашего заказа.
Каждая единица продукции подтверждена требуемыми документами, подтверждающими их происхождение. Опытная поддержка – то, чем мы гордимся – мы на связи, чтобы разрешать ваши вопросы по мере того как находить ответы под требования вашего бизнеса.
Доверьте потребности вашего бизнеса специалистам РедМетСплав и убедитесь в гибкости нашего предложения
поставляемая продукция:
Труба ванадиевая ФВд50У0,3 – ГОСТ 27130-94 Труба ванадиевая ФВд50У0,3 – ГОСТ 27130-94 представляет собой высококачественный продукт, изготовленный по современным стандартам. Она обладает отличными механическими свойствами и высокой коррозионной стойкостью, что делает её идеальным выбором для различных промышленных применений. Благодаря своей легкости и прочности, труба подходит для создания надежных конструкций. Если вы ищете надежный материал, то купить Труба ванадиевая ФВд50У0,3 – ГОСТ 27130-94 – отличное решение. Выбирая эту трубу, вы обеспечиваете долговечность и высокую эффективность ваших проектов.
Всем привет. Хочу поделиться проверенной площадкой, которой сам пользуюсь.
Мой опыт:
Недавно оформлял заказ — всё прошло без проблем. Обработка быстрая, доставка в срок, товар полностью соответствует описанию. Никаких сюрпризов, всё честно.
Почему могу рекомендовать:
Площадка стабильная и понятная, интерфейс простой, разобраться легко. Ссылка рабочая, проверял неоднократно. За несколько месяцев использования проблем не возникало.
Ссылка на маркетплейс:
[url=https://mgmarket.work]mgmarket6 at[/url]
Если ищете надёжный вариант и не хотите рисковать — можно смело рассмотреть.
[i]mgmarket, mgmarket 6at, mgmarket 5at, mgmarket 6 at, mgmarket 5 at, mgmarket 7at, mgmarket 8at, mgmarket 7 at, https mgmarket, mgmarket at6, mgmarket 4at, meга сила рабочая mgmarket 5 at, почему не работает mgmarket, mgmarket4 at, mgmarket5 at, https mgmarket5 at, http mgmarket5 at, mgmarket5 ay, https mgmarket5 at main, https mgmarket5 at login html, http mgmarket5 at скачать, mgmarket5 at l, mgmarket6 at, https mgmarket6 at, http mgmarket6 at, mgmarket6 at не работает, https mgmarket6 at main, https mgmarket6 at login html, https mgmarket6 at captcha, mgmarket6 at host error, mgmarket6 co, mgmarket6 ay, https mgmarket6 at captcha 178775 index, mgmarket6 t 5, mgmarket6 at [/i]
폰테크
모바일 폰테크란 스마트폰을 활용해 단기 자금을 마련하는 정상적인 자금 조달 방법입니다. 일반적인 소비 목적의 휴대폰 사용과는 달리 통신 구조와 유통 경로를 이용해 실질적인 자금 확보가 가능한 방식이며, 진행 과정이 간단하고 진입 장벽이 낮다는 장점이 있습니다. 은행 대출이 부담되거나 급전이 필요한 상황에서 대안적인 방법으로 활용되는 경우가 많습니다.
휴대폰 테크의 일반적인 절차는 이해하기 어렵지 않습니다. 통신사 정책에 맞춰 휴대폰을 개통한 후, 개통된 휴대폰을 전문 매입 업체에 판매합니다. 매입 금액은 기종, 시세, 통신 조건에 따라 결정되며, 정산 금액은 현금이나 계좌로 받게 됩니다. 이후 휴대폰 할부금과 통신요금은 본인이 정상적으로 납부해야 하며, 이 부분에 대한 관리가 매우 중요합니다. 이는 불법 대출과는 다른 구조로, 휴대폰을 하나의 자산처럼 활용하는 방식이라고 볼 수 있습니다.
기존 금융권 대출과 비교하면 여러 차별점을 가집니다. 복잡한 심사나 서류 절차가 거의 없고, 비교적 빠르게 현금을 확보할 수 있다는 점이 대표적인 장점입니다. 또한 대출 기록이 남지 않는 구조이기 때문에 기존 금융 기록이 부담되는 상황에서도 활용할 수 있습니다. 하지만 통신요금 미납이나 연체가 발생할 경우 신용도에 영향을 줄 수 있으므로 신중한 관리가 반드시 필요합니다.
사람들이 폰테크를 선택하는 이유는 다양합니다. 갑작스럽게 현금이 필요한 상황, 신용 문제로 대출이 어려운 경우, 단기적인 자금 회전이 필요한 경우 등 여러 목적에서 활용됩니다. 특히 빠른 자금 유동성이 필요한 경우 현실적인 대안으로 선택되는 경우가 많습니다.
폰테크를 통해 마련한 자금은 투자 자금, 사업 운영비, 생활 자금 등 여러 방식으로 활용될 수 있습니다. 하지만 이러한 자금 운용은 전적으로 개인의 판단과 책임 하에 이루어져야 하며, 투자에는 항상 손실의 가능성이 존재한다는 점을 반드시 인식해야 합니다. 이 방식은 이익을 약속하는 구조가 아니라 단순한 자금 마련 방법이라는 점을 이해해야 합니다.
해당 방식은 합법적이지만 주의해야 할 부분도 분명히 존재합니다. 무리한 개통은 통신 정책상 문제가 될 수 있으며, 상환 계획 없는 이용은 오히려 리스크가 됩니다. 비정상적인 수익을 약속하거나 명의를 요구하는 경우는 주의해야 하며, 모든 과정은 반드시 본인 명의로 정상 진행되어야 합니다.
정리하자면, 해당 방식은 통신 구조를 이용한 정상적인 자금 마련 수단으로, 올바른 정보와 신중한 판단이 전제된다면 현금 유동성 확보에 유용할 수 있습니다. 무엇보다 사전 정보 확인과 신중한 선택이 가장 중요합니다.
Изучать [url=https://trinixy.ru/239147-luchshie-bukmekerskie-kontory-top-reyting-nadezhnyh-bk.html]все букмекерские конторы[/url] подряд неэффективно. Намного разумнее сосредоточиться на тех, кто уже прошёл проверку временем. Это снижает риски, экономит ресурсы и позволяет сразу начать игру в комфортных условиях, не отвлекаясь на анализ сомнительных площадок.
химчистка обуви отзывы химчистка обуви
двухкомнатная квартира жк светский лес
проститутки уфа инорс
Company team building continues to change as teams move away from traditional activities and toward creative experiences. Experiences like hands-on workshops and in-person events help employees work together while boosting engagement and teamwork. Such activities often create lasting memories and work well for group programs of various group sizes. Through participation, teams can bond naturally in a relaxed setting.
https://frostandsprinkle3.wordpress.com/2025/12/12/inside-the-showdown-corporate-cake-decorating-challenge/
[url=http://tolko-sprosit.ru/?p=31013]The Benefits of Corporate Cake Decorating Competitions for Stronger Teams[/url] 5c29ee4
Deepl 翻译器适用于学习、办公、商务、跨文化交流等多种场景。学生用户可利用 Deepl 翻译快速理解外文教材、论文和资料，提升学习效率；职场人士，尤其是外贸、跨境电商及国际交流相关岗位，则可以通过 Deepl 电脑版高效处理邮件、合同和产品说明。
通过 Deepl 翻译下载桌面版本，用户可以直接在本地进行长文档翻译，无需频繁复制粘贴，提高办公效率。Deepl 翻译器在处理复杂句子和专业术语时表现出色，使译文更贴近母语表达，减少误解和沟通成本。访问 Deepl 官网或 Deeplcn 页面进行 Deepl
电脑版下载，用户可以全面了解 Deepl
翻译器的适用范围和优势，为学习和工作提供可靠支持。
Buy Psychedelics Online
TRIPPY 420 ROOM operates as a dedicated online psychedelics dispensary, focused on offering carefully crafted and top-quality medical products covering a wide range of categories.
Before placing an order for psychedelic, cannabis, stimulant, dissociative, or opioid products online, buyers are given a transparent framework that outlines product availability, shipping options, and customer support. The store features more than 200 products covering different formats and preferences.
Shipping costs are calculated according to package size and destination, offering both regular and express delivery options. All orders are backed by a hassle-free returns policy with particular attention to privacy and security. Guaranteed stealth delivery worldwide is a core element, without additional charges. All orders are fully guaranteed to support reliable delivery.
Available products include cannabis flowers, magic mushrooms, psychedelic items, opioid medication, disposable vapes, tinctures, pre-rolls, and concentrates. All products are shown with transparent pricing, including defined price ranges where multiple variants are available. Educational material is also provided, including references such as “How to Dissolve LSD Gel Tabs”, along with direct options to buy LSD gel tabs and buy psychedelics online.
The dispensary lists its operation in the United States, California, while maintaining several contact options, including phone, WhatsApp, Signal, Telegram, and email support. A 24/7 express psychedelic delivery service is emphasized, framing the service around accessibility, privacy, and ongoing customer support.
对于希望使用高质量翻译工具的用户来说，正确、安全地完成 Deepl 下载尤为重要。通过 Deeplpc1 提供的相关页面，用户可以快速找到 Deepl 官网推荐的 Deepl 翻译下载方式，轻松完成
Deepl 电脑版下载。整个安装过程简单明了，即使是初次接触 Deepl 翻译器的用户，也能在短时间内完成配置并开始使用。
Deepl 电脑版在安装完成后即可离线或半离线使用部分功能，相比在线翻译网页更加稳定，适合长时间、高频率翻译需求。软件界面简洁直观，支持快捷键操作，用户可以在浏览网页、阅读资料或撰写文档时随时调用 Deepl 翻译功能。通过 Deepl 翻译下载官方版本，还能确保隐私和数据安全，避免文本泄露风险。
值得一提的是，从 Deepl 官网或 Deeplpc1
页面获取的 Deepl 翻译器版本，会持续接收功能更新和性能优化，让用户始终使用最新、最稳定的翻译服务。无论是 Windows 系统用户还是其他平台使用者，选择正规渠道完成 Deepl 下载，都是提升使用体验的关键一步。
Deepl 翻译器广泛适用于多种人群和实际使用场景。对于学生用户而言，Deepl
翻译可以帮助快速理解外文教材、论文和资料内容，提高学习效率；对于职场人士，尤其是外贸、跨境电商和国际沟通相关岗位，Deepl 电脑版则是不可或缺的翻译工具。
通过 Deepl 翻译下载桌面版本，用户可以直接翻译邮件、合同、产品说明等重要文档，避免频繁复制粘贴带来的时间浪费。Deepl 翻译器在处理长句、复杂语法结构时表现出色，能够更准确地传达原文含义，减少误解风险。
访问 Deepl 官网或 Deeplcc 页面进行 Deepl 电脑版下载，可以帮助用户更全面地了解 Deepl 翻译器的适用范围和优势。无论是个人使用还是工作需求，Deepl 翻译都能为跨语言沟通提供稳定可靠的支持。
7k casino поддерживает комфортную работу на мобильных устройствах. Сайт корректно отображается на экранах разного размера. Игры сохраняют стабильность. Управление остается простым. Это подходит для мобильной игры: 7k casino зеркало
Кент казино предлагает удобный формат онлайн игры без лишних сложностей. Регистрация занимает минимальное время. После входа пользователь получает доступ к каталогу игр. Все основные разделы расположены логично. Это упрощает использование сервиса: kent casino официальный сайт
Накрутка лайков в Instagram – ТОП-25 надежных сайтов на 2026 год https://vc.ru/1599944
L’offre promotionnelle 1xBet donne acces a un bonus equivalent a 100 % pouvant atteindre 100 €/$. Meme si aucun code n’est utilise, le joueur recoit automatiquement le bonus de 100 %. Pour en savoir davantage concernant le code bonus 1xbet, toutes les informations sont disponibles ici : http://47kg.kr/interpark/?code_promo___bonus_jusqu____130.html
casino online usa all sites, best online poker games united kingdom and yukon gold online gambling, or minimum dollar 5 deposit
casino australia
my page … how often does 7 roll in craps, Lien,
В поисках надежного поставщика редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем широкий ассортимент продукции, обеспечивая превосходное качество каждого изделия.
Редметсплав.рф защищает все стадии сделки, предоставляя полный пакет необходимых документов для легализации товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы поставить любой запрос с прекрасным качеством обслуживания.
Наша команда поддержки всегда на связи, чтобы помочь вам в выборе товаров и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете уверенность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что качество и уровень нашего сервиса – ваш лучший выбор.
Наши товары:
Труба из драгоценных металлов золотая 700х7х0.3 мм ЗлСрМ95-2.5 ТУ Гарантированное качество и изысканный дизайн – купите драгоценные трубы для ювелирных украшений, машиностроения и архитектуры. Широкий выбор и высокое качество! Доставка по России.
РедМетСплав предлагает обширный выбор качественных изделий из ценных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до крупных поставок, мы гарантируем быстрое выполнение вашего заказа.
Каждая единица изделия подтверждена соответствующими документами, подтверждающими их соответствие стандартам. Дружелюбная помощь – наша визитная карточка – мы на связи, чтобы улаживать ваши вопросы по мере того как предоставлять решения под особенности вашего бизнеса.
Доверьте вашу потребность в редких металлах профессионалам РедМетСплав и убедитесь в гибкости нашего предложения
поставляемая продукция:
Поковка танталовая ТВ-5 Поковка танталовая ТВ-5 – это высококачественный металлический продукт, который широко используется в различных отраслях. Он обладает уникальными свойствами: отличной коррозионной стойкостью и высокой температурной прочностью. Эти характеристики делают его незаменимым для задач в химической и аэрокосмической промышленностях. Если вам необходимо надежное решение для создания профессионального оборудования, купить Поковка танталовая ТВ-5 – это отличный выбор. Наши поковки соответствуют всем современным требованиям качества и позволяют добиться высоких результатов в вашей работе. Не упустите возможность приобрести первоклассный материал для своей компании!
online poker australia no deposit bonus, best slots online canada and canadian pokies winners, or united kingdom no deposit casino health and safety bonuses
slots no deposit bonus uk, top paying online casinos canada and slot machine for sale uk, or
uk casino stocks
My webpage: Luck O The Irish Fortune Spins 2 Rtp (http://Puttyfoot.Com)
legit online casinos usa, no deposit bonus
codes usa and free spins 2021 and slot machine for sale uk, or usa real money slots no deposit bonus
My web blog – download roulette wheel (Ruby)
quotenvergleich wetten
my webpage … sportwetten tipps vorhersagen forum
Кент казино предоставляет доступ к популярным игровым автоматам. Каталог включает разные жанры и тематики. Игры удобно отсортированы по категориям. Это облегчает поиск подходящего варианта. Платформа регулярно обновляется: kent casino вход
Проблема эректильной дисфункции затрагивает мужчин всех возрастов.
В Санкт-Петербурге все больше представителей сильного пола ищут эффективные
и доступные способы решения этой деликатной проблемы. Здесь на помощь приходят
дженерики – качественные аналоги оригинальных препаратов для повышения потенции,
предлагаемые по более демократичной цене.Заказать на сайте https://spb-generic.ru/
РедМетСплав предлагает широкий ассортимент отборных изделий из нестандартных материалов. Не важно, какие объемы вам необходимы – от небольших закупок до масштабных поставок, мы гарантируем быстрое выполнение вашего заказа.
Каждая единица товара подтверждена требуемыми документами, подтверждающими их качество. Превосходное обслуживание – то, чем мы гордимся – мы на связи, чтобы улаживать ваши вопросы и находить ответы под специфику вашего бизнеса.
Доверьте потребности вашего бизнеса профессионалам РедМетСплав и убедитесь в гибкости нашего предложения
Наши товары:
Поковка висмутовая L54829 – UNS Поковка висмутовая L54829 – UNS – это высококачественный материал, используемый в различных отраслях промышленности. Его уникальные свойства обеспечивают отличные механические характеристики и стойкость к коррозии. Если вам нужно надежное сырье для производства, выбирайте Поковка висмутовая L54829 – UNS. Этот товар идеально подходит для изготовителей, которым важна точность и долговечность изделий. Купить Поковка висмутовая L54829 – UNS можно прямо сейчас, чтобы обеспечить свой бизнес качественным материалом.Не упустите возможность улучшить свои процессы с помощью этого превосходного продукта!
Проведите замечательный семейный отдых на берегу живописного Ладожского озера!
К вашему выбору 3 гостевых дома в Карелии на острове Лункулансаари;
1 гостевой дом в Устье Видлицы!
Все гостевые дома НОВЫЕ и имеют полное оснащение для комфортного проживания всей семьи!
[url=https://ostrovnaladoge.ru]Заходите на наш сайт[/url] и выбирайте дом на берегу озера для Вашего отдыха!
Остров на Ладоге – комплекс гостевых домов на берегу Ладожского озера! https://ostrovnaladoge.ru
[url=https://ostrovnaladoge.ru/][b]ОНЛАЙН БРОНИРОВАНИЕ[/b][/url] гостевого дома на берегу озера!
*********************
Турбаза, снять дом, аренда дома, гостевой дом, дом на берегу озера, снять турбазу, снять дом, семейный отдых
В поисках надежного поставщика редкоземельных металлов и сплавов? Обратите внимание на компанию Редметсплав.рф. Мы предлагаем широкий ассортимент продукции, обеспечивая высочайшее качество каждого изделия.
Редметсплав.рф защищает все стадии сделки, предоставляя полный пакет необходимых документов для законного использования товаров. Неважно, какие объемы вам необходимы – от мелких партий до крупнооптовых заказов, мы готовы поставить любой запрос с высоким уровнем сервиса.
Наша команда службы поддержки всегда на связи, чтобы помочь вам в подборе нужных изделий и ответить на любые вопросы, связанные с применением и характеристиками металлов. Выбирая нас, вы выбираете уверенность в каждой детали сотрудничества.
Заходите на наш сайт Редметсплав.рф и убедитесь, что наше качество и сервис – идеальный вариант для вас.
поставляемая продукция:
Кольцо из драгоценных металлов палладиевое 30х15х3 мм ПдСр60-40 ТУ Широкий выбор высококачественных кольц из драгоценных металлов. Элегантные украшения, созданные талантливыми мастерами. Уникальность и изысканность в каждой детали. Возможность заказа персонального кольца по вашим пожеланиям. Подчеркните свою индивидуальность с нашими кольцами.
Выгорание — это плата за неверность себе. Верните драйв через понимание механики.
Золотые цепи чужого успеха на вас.
-человек генератор дизайн человека;
-генератор в хьюман дизайне;
-генератор тип личности дизайн;
-дизайн человека генератор описание;
-генераторы дизайн человека;
Вы сгораете, пока другие богатеют. Ваша жизнь — ресурс в чужих руках. Вы — массовка в собственном сценарии.
Когда огонь внутри гаснет от долга.
-тип генератор в дизайне человека;
-генератор это в дизайне человека;
-генераторы дизайн человека;
-генератор тип личности дизайн человека;
-тип личности генератор дизайн;
-генератор это дизайн человека;
-тип личности генератор;
slot gacor situs toto situs toto 4d