今天介绍的是强化学习的基本问题--多臂老虎机(Multi-arm\ Bandits)。
在开始介绍多臂老虎机问题之前,我们需要先搞清楚这个问题在强化学习问题中的位置。这就涉及到了一个关键的概念 -- associative,我们知道强化学习是涉及到多个场景的,智能体学习的目标是掌握在不同场景下的最优动作。但多臂老虎机问题作为最基础的强化学习问题,是 unassociative 的,也就是说在该问题中只有一个状态,我们只需要考虑如何优化在这一个状态下的决策。
多臂老虎机问题
现在让我们考虑这样一个问题:我们有 n 个不同的选项或操作,现在我们可以重复地进行操作,并且每次操作之间互不相关。在每次选择之后,我们都会收到一个奖励 r,对于一个确定的操作所带来的奖励 r 服从一个固定的概率分布,我们的目标是在某个时间段内最大化我们可能得到的总奖励值。
这就是多臂老虎机问题的原始形式,每个动作选择就像是老虎机的一个杠杆,奖励是中奖的回报。通过重复的行动选择,我们通过将操作集中在最佳杠杆上来最大化收益。如果你知道每个动作的价值,那么解决多臂老虎机问题就很简单了:总是会选择价值最高的动作。当然,对于每个操作所能够带来的奖励的概率分布,我们一开始是不知道的!
如果我们用最简单的方法对每个操作可能带来的收益进行一个评估,比如根据已经观测到的数据直接求均值,那么在每个时间步我们都能够找到一个估计值最大的动作。这个动作被称为 greedy\ action。如果当前的决策是这个 greedy\ action,那么就说我们当前是在 exploiting;相反,如果我们当前的决策并非直接选取 greedy\ action,那么就说我们当前是在 exploring,因为这样可以增强智能体对于其他动作的认知,或许可以增强对其他的动作的估计,从而产生新的 greedy\ action。exploiting 是单步最大化预期回报的最佳做法,但从长远来看,exploring 可能会产生更大的总回报。平衡 exploring 和 exploiting 是强化学习中出现的一个独特挑战,多臂老虎机问题的简单性使我们能够更加清晰地感受这一特点。
Action-Value方法
事实上,我们应该关心的一个问题是:如何在长期的选择过程中获得更大的收益。这就要求我们学会利用历史信息以便在未来做出更优的决策。一个很简单的方法就是:使用历史奖励值的平均对每个动作进行评估。不妨设每个动作 a 的真实奖励的均值为 q(a),我们对每个动作的估计值为 Q_t(a),直到 t 时刻,动作 a 被执行了 N_t(a) 次,而这 N_t(a) 次获得的奖励值记作 \{R_1,\cdots,R_{N_t(a)}\}。于是,我们可以用如下的方式计算对动作 a 的估计
Q_t(a) = \frac{R_1 + R_2 + \cdots + R_{N_t(a)}}{N_t(a)}.我们应该考虑到一些特殊情况,比如在初始时,N_t(a)=0,这个时候可以设 Q(a) = 0,我们称这种方法为 sample\ average。根据大数定理,当 N_t(a) \rightarrow \infty 时,Q_t(a) 概率为 1 的接近于 q(a),因此,尽管这个方法简单,但却是十分有效的,只要我们能够保证每个动作被采样过无数次。
此时,我们就可以形式化地定义 greedy\ aciton了
A_t^* = \arg\max_a Q_t(a).直接依托于这个公式的方法就叫做 greedy\ methods,这种方法无时无刻不在 exploiting。
从长远来看,greedy\ methods 并不是一个比较好的策略,因为有可能错失一些比价优秀的动作。于是,一个很直接的想法就是,每次决策时以一定的概率 \epsilon 从所有的动作中进行随机选择,基于这种思想的方法就是 \epsilon-greedy 方法。\epsilon-greedy 方法可以保证无论进行到第几次决策,每个动作都有一定的概率被执行,这也就满足了大数定律的要求。于是,在经过了足够长时间的训练之后,\epsilon-greedy 方法将能够获知每个动作的真实收益。
greedy 方法和 \epsilon-greedy 方法对比
设计一个简单的实验对两种方法进行验证,先来说说实验的基本设定:
- 准备2000个随机生成的多臂老虎机,
n=10,每个老虎机都有 10 个动作可供选择,也就是说每个老虎机有 10 种不同的可能的奖励。 - 老虎机的每个动作对应的奖励是从一个标准正态分布中生成的,也就是
q(a)\sim N(0,1)。 - 在
t时刻,当我们选择了一个动作A_t之后,从环境中获得的奖励是q(A_t)再加上一个来自标准正态分布的噪声,也就是R_t \sim N(q(A_t),1)。 - 使用刚开始随机生成的 2000 个老虎机同时进行实验,每个老虎机都是一组单独的实验,每组实验进行 1000 轮。
值得提醒的是,这里不同的老虎机之间并没有什么关系,只是 2000 组独立重复的实验而已;另外,第二步事实上是在设定每个动作的奖励的均值,第三步则是设定方差,因此最后每个动作的奖励还是一个不确定的分布,而非一个确定的值(除非方差设置为0)。
现在,我们分别令 \epsilon = \{0,0.01,0.1\} 运行上面的实验,注意 \epsilon=0 实际上就是 greedy\ method,得到的实验结果如下所示:
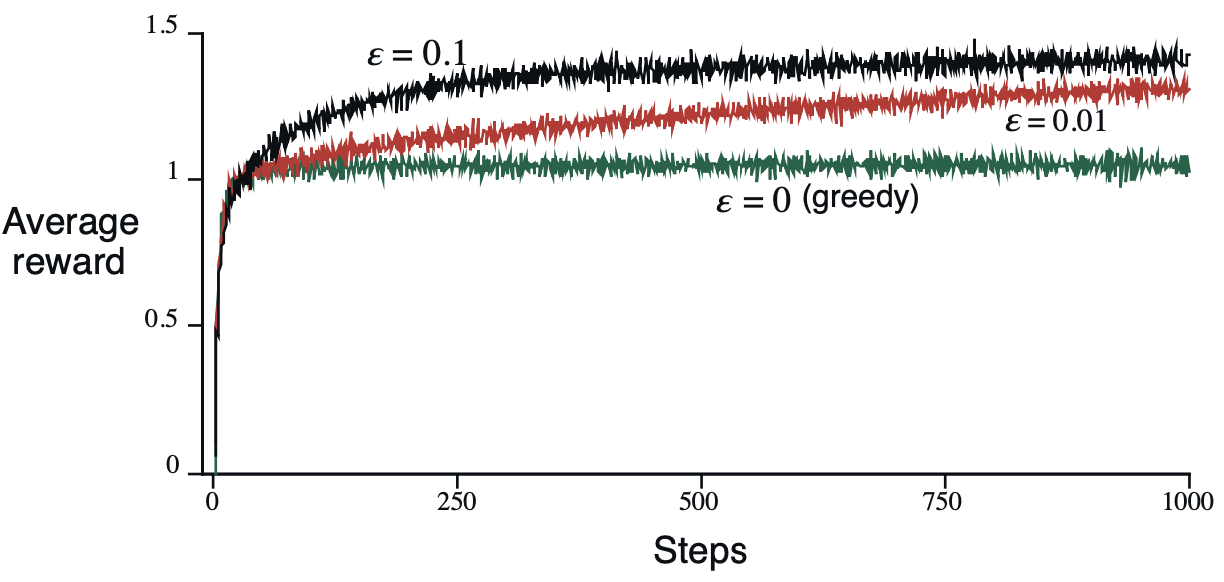
显然,\epsilon=0.01在未来可以带来最好的收益,只是优化速度比较缓慢~
观察实验结果,我们可能会有一个问题:greedy\ method 为啥能够发生变化呢?按照我们之前的逻辑,难道不是第一次随机选了一个动作之后就确定了么?事实上,greedy\ method 具有很大的不确定性,假设所有的动作估计值都初始化为0,而且第一次选出来的动作 a 获得的奖励如果是小于 0 的,那么下次该方法就会尝试别的动作,直到遇到了某个奖励值持续稳定在 0 以上的动作,其后基本就不会再发生什么变化了。对 greedy\ method 而言,比较糟糕的一种情况就是,刚一开始就随机到了一个真实奖励均值略大于 0 的动作,那么很大概率以后基本上就会采取这个动作了。事实上,通过设定每个动作初始估计值可以对 greedy\ method 进行很好的引导,这在后面会提到。
增量方法
实际上,增量方法并不是一个新的方法,而是对现有方法的一个优化。采用增量的实现形式,可以节省更多的计算资源,并且从最终的公式的表达形式我们还可以更加直观地理解 sample\ average方法的思想内涵。
我们前面已经提到过,我们对每个动作的估计值是历史奖励值的平均,但是大数定理告诉我们,我们将会需要很长时间的运行才能得到比较精确的结果。于是,我们不希望,每次都对 Q_t(a) 重头计算,这样最终每个动作的计算复杂度将会达到平方级别。只需要对计算公式进行简单的化简就可以实现简单的常数时间迭代,下面的分析都是针对同一个动作而言的,因此对符号进行了一定程度上的简写:
\begin{aligned}
Q_{k+1} &= \frac{1}{k}\sum_{i=1}^{k}R_i\\
&= \frac{1}{k}(R_k+\sum_{i=1}^{k-1}R_i)\\
&= \frac{1}{k}(R_k+(k-1)Q_k)\\
&=Q_k + \frac{1}{k}[R_k - Q_k]\\
\end{aligned}因此,最终我们只要额外记录下动作 a 被执行的次数就可以实现上面的更新了。
进一步地,将 1/k 理解为步长,R_k 理解为对 Q_k 的引导,我们的更新公式可以抽象为
NewEstimate \gets OldEstimate + StepSize[Target - OldEstimate].这就是增量方法的本质,步长取 1/k 只是一种特殊的使用方法罢了。
nonstationary 问题
上面我们考虑的问题都是 stationary 的,也就是每个老虎机无论何时它的每个动作的奖励的概率分布都是固定的。现在,我们借助刚说过的增量的思想来说说如何处理 nonstationary 的场景。
这个时候,如果再取步长为 1/k 可能就比较尴尬了,因为越往后步长越小,智能体获取最新信息的能力一直在下降,这样的智能体并不适合处理实时变化的场景。实际上,直接取步长为常数 \alpha\in(0,1] 就是一个不错的选择。我们利用前述的增量公式对其自身进行递归展开,如下所示:
Q_{k+1} = (1-\alpha)^kQ_1 + \sum_{i=1}^{k}\alpha(1-\alpha)^{k-i}R_i.我们发现,对于时间比较久远的奖励值 R_i 的系数 (1-\alpha)^{k-i} 会慢慢变得越来越小,相反,对最新的奖励值重视程度比较高。除此之外,所有的系数之和为 1,也保证了算法的稳定性。
初始值设定
我们已经分析过的所有方法基本上都会受动作估计值的初始值的影响,但是影响有大有小。对于 \epsilon-greedy 方法而言,不同的初始值可能只是影响刚开始性能曲线增长的速度,但是从长远来看,每个动作都会被执行无数次,所以到了后面初始值的影响就不大了。事实上,greedy 方法受初始值的影响最大,一个好的初始值可以引导 greedy 方法对未知的动作进行探索,而一个比较差的初始值则可能直接引发灾难。下面,我们分析一下greedy 方法。
当初始值设置为 \infty 时,每个动作的估计值都会小于 \infty,因而 greedy 方法会在一开始的 n 次迭代将所有的工作都尝试一遍,最后选择估计值最优的那个动作,这样每个动作至少都被探索过一次,试想如果我们一开始的实验设定就是方差为0,那么一次探索就可以知道每个动作的真实奖励,也就是获得了最优的策略;而当初始值设置为 -\infty 时,第一次随机到的动作基本上也就是以后都会采取的动作了。因此,设定一个较大的初始值往往会刺激 greedy 方法进行更多的探索,从而变得更加行之有效。
基于置信区间上界的动作选择 Upper-Confidence-Bound
前面讲过的所有方法本质上都是 sample\ average,这里再提出另外一种方法,它除了基于历史对动作的价值进行进行评估之外还对每个动作的潜力进行评估。不过这里对潜力的评估比较简单,公式如下:
A_t = \arg\max_a\left[Q_t(a)+c\sqrt{\frac{\ln t}{N_t(a)}}\right].观察公式我们会发现,那些很久没有被采样过的方法将会被重新选择出来,因为随着时间的推移,很少被采样的动作的补充项将会变得很大,于是乎,这个方法也可以保证大数定律的条件。
我们可以将这种方法理解为 greedy 方法的一种改进,实践表明,UCB 通常比 \epsilon-greedy 更加高效。
梯度方法 Grandient\ Bandits
梯度方法和前面已经讲过的方法关系不是很大,这里仍然是 nonstationary 的场景,我们为每个动作分配一个可训练的偏好指标 H_t(a),偏好指标越大,我们在下一次决策时就越有可能选择到这个动作。在每一次进行决策时使用的是由这个偏好指标生成的概率分布:
\pi_t(a)\gets Pr[A_t = a] = \frac{e^{H_t(a)}}{\sum_b e^{H_t(b)}}.下面,我们使用类似于梯度下降的想法来更新每个动作的偏好 H_t(a)。
这要求我们选定一个优化的目标,很自然地,我们希望按照概率分布 \pi_t(a) 可以获得尽可能大的收益的期望,也就是
\max_{\pi} E[R_t] = \sum_b{\pi_t(b)q(b)}.但是,一个实际的问题是 q(b) 未知,我们先假装已经知道了,继续往下推~
根据梯度下降的思想,偏好指标的更新公式应当为
H_{t+1}(a) = H_{t}(a) + \alpha\frac{\partial E[R_t]}{\partial H_t(a)}.于是,我们尝试对梯度项进行分析和近似:
\begin{aligned}
\frac{\partial E[R_t]}{\partial H_t(a)} &= \frac{\partial}{\partial H_t(a)}[\sum_b{\pi_t(b)q(b)}]\\
&=\sum_b{q(b)\frac{\partial\pi_t(b)}{\partial H_t(a)}}\\
&=\sum_b{(q(b) - X_t)\frac{\partial\pi_t(b)}{\partial H_t(a)}}
\end{aligned}其中,X_t 是一个与动作无关的项,而 \sum_b{\frac{\partial\pi_t(b)}{\partial H_t(a)}}=0,所以我们可以有上面最后一步的推导,这其实就是softmax的求导的一个自然结果,或者也可以理解为先求和在求导,你会发现求和的结果是1,所以导数不变。
继续,将动作表示为一个服从概率分布 \pi_t(a) 的随机变量 A_t,并使用 R_t 表示对 q(A_t) 的估计,有如下推导:
\begin{aligned}
&=\sum_b{(q(b) - X_t)\frac{\partial\pi_t(b)}{\partial H_t(a)}}\\
&=\sum_b{\pi_t(b)(q(b) - X_t)\frac{\partial\pi_t(b)}{\partial H_t(a)}}/\pi_t(b)\\
&=E[(q(A_t) - X_t)\frac{\partial\pi_t(A_t)}{\partial H_t(a)}/\pi_t(A_t)]\\
&\approx E[(R_t - X_t)\frac{\partial\pi_t(A_t)}{\partial H_t(a)}/\pi_t(A_t)]\\
&=(R_t - X_t)E[\frac{\partial\pi_t(A_t)}{\partial H_t(a)}/\pi_t(A_t)]
\end{aligned}令 X_t = \bar{R}_t,剩下的就是softmax求导了,最后可得:
(R_t - \bar{R}_t)(\mathbb{I}_{a=A_t}-\pi_t(a))将计算结果代入梯度下降方程,可得:
H_{t+1}(a) = H_{t}(a) + \alpha(R_t - \bar{R}_t)(\mathbb{I}_{a=A_t}-\pi_t(a))其中,\mathbb{I}_{a=A_t} = 1 \Leftrightarrow a = A_t。
总结
今天,以多臂老虎机为强化学习的入门例子介绍了几种常用的方法极其思想,下周是有限马尔科夫决策过程,敬请期待~
