这一章将介绍在本书其余部分将要解决的问题。事实上,这个问题定义了强化学习领域:任何适合解决这个问题的方法,我们都可以认为是强化学习方法。
本章的目标是从广义上描述强化学习问题,这包括:描述强化学习问题的数学形式、介绍强化学习问题的关键元素,例如值函数和贝尔曼方程等、讨论强化学习文中的一些权衡和挑战。
首先,我们来分享一些basic的东西,包括关键元素、强化学习问题的简单分类以及符号定义。
Basic
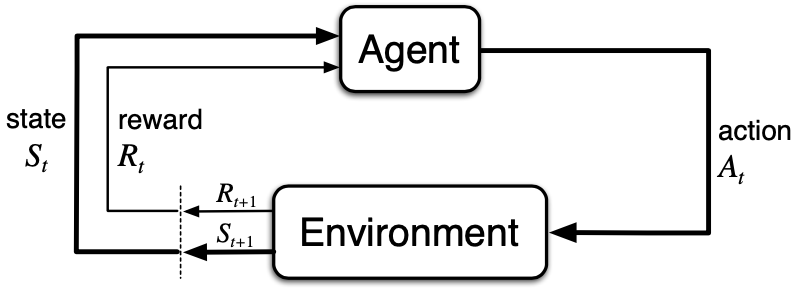
首先是两个主体:Agent和Environment,两个主体之间的交互关系如图所示。通常Environment决定了我们要解决的问题,Agent就是我们要训练的来解决强化学习问题的主体。两个主体进行交互,是通过动作、状态、奖励实现的。
现在更具体地说说Agent和Environment在离散时间序列中的每一次交互:在每个时间步 t(t = 1,2,\cdots),Agent接收Environment的状态表示,S_t \in \mathcal{S},其中 \mathcal{S} 是可能状态的集合,并在此基础上选择一个动作 A_t \in \mathcal{A}(S_t),其中 \mathcal{A}(S_t) 是状态 S_t 下可采取的动作集合。一个时间步后,Agent收到一个数字奖励,R_{t+1} \in R \subset \mathbb{R},并处于一个新状态 S_{t+1}。
在每个时间步,Agent 维护一个从状态到可能动作的概率的映射。这种映射称为Agent的策略,记为 \pi_t,其中 \pi_t(a|s) 是在 S_t = s 时 A_t = a 的概率。强化学习方法的核心就是指导Agent根据其经验不断地优化自己的策略,Agent的目标就是最大化它在长期内获得的总奖励。
现在,我们来说说强化学习问题的目标和 reward 之间的关系,我们的目标通常都是非形式化的,reward 的设定正是为了将我们的非形式化目标可以直接与强化学习框架结合起来。关于这一点,书中提到了 reward\ hypothesis:
That all of what we mean by goals and purposes can be well thought of as the maximization of the expected value of the cu- mulative sum of a received scalar signal (called reward).
基于训练目标的描述,在第 t 个时间步,回报有如下的形式化表示:
G_t = R_{t+1} + R_{t+2} + R_{t+3} + \cdots + R_T,再加上折扣的概念 \gamma \in [0,1],我们可以将回报进一步地表述为如下的形式:
G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^{\infty}\gamma^k R_{t+k+1}. 此外,强化学习过程还被分为两种不同的形式:有限的和无限的过程。这里为了将两种形式下的优化目标进行统一描述,我们尝试通过设置一个 aborbing\ state 将有限的过程表示为无限的过程,aborbing\ state 事实上就是终止状态,在这个状态之后,所有的奖励值都设置为 0 ,次状态设置为其本身即可。
马尔科夫性质
理想情况下,我们想要的是一个可以总结过去所有经验的状态,至少应该保留进行决策所需的所有相关信息。这通常需要的不仅仅是当前时间步的直接感受,还有一些历史信息。成功保留所有相关信息的状态称为马尔可夫的或具有马尔可夫性质。这有时也被称为 independence\ of\ path 属性,因为重要的是当前状态,而已经与历史状态关系不大了,因为当前状态已经包含了我们所需要的所有信息。
为了通过简单的数学形式表示马尔科夫性质,这里假设状态数为有限个。考虑在第 t+1 个时间步,Environment 会对第 t 个时间步的action做出什么样的反馈,这个反馈可能取决于之前发生过的所有的交互。因此,使用一个概率分布来表示这个事情就是
Pr\{R_{t+1}=r,S_{t+1}=s'|S_0,A_0,R_1,\cdots,S_{t-1},A_{t-1},R_t,S_t,A_t\}.对于所有的 r, s' 和 S_0,A_0,R_1,\cdots,S_{t-1},A_{t-1},R_t,S_t,A_t 的可能值,都有这样一个概率存在。
当然,如果状态具有马尔科夫性质,也就是说每个次状态都只与当前状态有关,那我们的状态公式就可以表示为
p(s',r|s,a) = Pr\{R_{t+1}=r,S_{t+1}=s'|S_t,A_t\}.因此,从公式的角度来描述马尔科夫性质的话就是:一个问题的状态描述是马尔科夫的 当且仅当 上述两个式子相等。
Markov Decision Process
一个满足马尔科夫性质的强化学习任务就是 Markov Decision Process或者简写为 MDP,MDP有两个核心的概率公式:一个是 \pi(a|s),另一个是 p(s',r|s,a)。\pi(a|s) 是我们要训练得到的决策函数,p(s',r|s,a) 则主要是由环境决定的,虽然我们直观上想可能觉得在确定了状态以及该状态下的动作之后,次状态和奖励值将会是确定的,然而事实并非如此。因此,在考虑强化学习问题时也要将这个不确定的因素考虑进去。
p(s',r|s,a) 由环境决定,基于这个式子,我们可以推断出很多有用的变量值
比如期望的奖励值(针对特定的状态-动作对)
r(s,a) = E[R_{t+1}|S_t=s,A_t=a] = \sum_{r\in \mathcal{R}}r\sum_{s'\in\mathcal{S}}p(s',r|s,a),比如状态转移概率
p(s'|s,a) = Pr\{S_{t+1}=s'|S_t=s,A_t=a\}=\sum_{r\in \mathcal{R}}p(s',r|s,a)再比如期望的奖励值(针对特定的状态-动作-次状态三元组)
r(s,a,s') = E[R_{t+1}|S_t=s,A_t=a,S_{t+1}=s'] = \frac{\sum_{r\in \mathcal{R}}rp(s',r|s,a)}{p(s'|s,a)}.值函数 Value Function
所有的强化学习任务都需要对值函数进行评估,值函数有两个:状态值函数 v_\pi(s) 和 q_\pi(s,a),v_\pi(s) 是状态值函数,用于评估每个状态的好坏,q_\pi(s,a) 是动作值函数,用于评估每个状态下动作的好坏。先回忆一下之前说过的策略 \pi(a|s),说的是在状态 s 下采取不同的动作 a 的概率。在每个既定策略下,我们都可以用如下的形式表示值函数
v_{\pi}(s)=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right]=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s\right],\\
q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right]=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s, A_{t}=a\right].值函数可以基于经验进行评估,假设我们维护一个平均值,如果某个状态在训练过程中被遇到了无数次,那么这个估计的均值就可以被看做是对值函数的估计。
上面说的均值事实上是依托于当前状态与次状态之间的递推关系的,以状态值函数为例,我们有如下推导
\begin{aligned}
v_{\pi}(s) &=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right] \\
&=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s\right] \\
&=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \mid S_{t}=s\right]\\
&=\mathbb{E}_{\pi}\left[R_{t+1}\mid S_{t}=s\right]+\gamma\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \mid S_{t}=s\right]\\
&=\sum_{a} \pi(a \mid s) \sum_{r} p\left(r \mid s, a\right)r+
\gamma\sum_{a} \pi(a \mid s) \sum_{s^{\prime}} p\left(s^{\prime}\mid s, a\right)\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \mid S_{t+1}=s^{\prime}\right]\\
&=\sum_{a} \pi(a \mid s) \sum_{r} \sum_{s^{\prime}} p\left(s^{\prime}, r \mid s, a\right)r+
\gamma\sum_{a} \pi(a \mid s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \mid S_{t+1}=s^{\prime}\right]\\
&=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right]
\end{aligned}这个式子被称为状态值函数的贝尔曼方程,它展示了状态与次状态的递推关系,在实际的优化过程中,正是借助这个式子使得每个状态的值不断地接近真实值。
最优值函数
是否存在最优值函数呢?如果我们定义了比较两个策略好坏的标准,那么理论上就存在最优策略。我们定义两个策略 \pi 和 \pi',\pi \geq \pi' 当且仅当 \forall s, v_\pi(s) \geq v_{\pi'}(s)。如果 \pi_* 是最优策略,那么就应该有
\forall s,\forall \pi,v_{*}(s) \geq v_{\pi}(s),其中 v_*(s) 表示最优策略下的值函数,上述不等关系也可以表示为
\forall s\in\mathcal{S}, v_*(s) = \max_\pi v_\pi(s),同样的,我们也可以有对动作值函数的类似表示
\forall s\in\mathcal{S},\forall a\in \mathcal{A}(s),q_*(s,a) = \max_\pi q_\pi(s,a).于是,我们可以得到状态值函数和动作值函数之间的递推关系以及当前状态与次状态之间的递推关系,这些递推关系都是在强化学习优化过程中的核心公式:
\begin{aligned}
v_{*}(s) &=\max _{a \in \mathcal{A}(s)} q_{\pi_{*}}(s, a) \\
&=\max _{a} \mathbb{E}_{\pi^{*}}\left[G_{t} \mid S_{t}=s, A_{t}=a\right] \\
&=\max _{a} \mathbb{E}_{\pi^{*}}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s, A_{t}=a\right] \\
&=\max _{a} \mathbb{E}_{\pi^{*}}\left[R_{t+1}+\gamma \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \mid S_{t}=s, A_{t}=a\right] \\
&=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{*}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \\
&=\max _{a \in \mathcal{A}(s)} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{*}\left(s^{\prime}\right)\right] .
\end{aligned}\begin{aligned}
q_{*}(s, a) &=\mathbb{E}\left[R_{t+1}+\gamma \max _{a^{\prime}} q_{*}\left(S_{t+1}, a^{\prime}\right) \mid S_{t}=s, A_{t}=a\right] \\
&=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right)\right]
\end{aligned}总结
以上就是MDP的基本知识,下次我们分享强化学习的迭代训练方法 -- Dynamic\ Programming。

It’s very interesting! If you need help, look here: ARA Agency
I am extremely impressed together with your writing skills and also with the structure to your weblog. Is this a paid subject matter or did you modify it your self? Either way keep up the excellent quality writing, it is uncommon to look a great weblog like this one nowadays!
buying legal steroids
References:
Valley.Md
Exklusive Sneaker Trends von JD Sports – jetzt die neuesten Modelle von Nike & adidas sichern.
Genieße tolle Deals in Essen & Trinken – von Snacks bis Getränke, alles für deinen Alltag.
Experience Brainy https://askbrainy.com the free & open-source AI assistant. Get real-time web search, deep research, and voice message support directly on Telegram and the web. No subscriptions, just powerful answers.
ifvod平台,专为海外华人设计,提供高清视频和直播服务。
超人和露易斯第二季高清完整版结合大数据AI分析,海外华人可免费观看最新热播剧集。
«СибСети» в Новосибирске предоставляют:
• интерактивное ТВ;
• Комплексный анализ доступных технологий в вашем доме
• Подбор оптимального тарифа под ваши задачи
• Анализ технической доступности по вашему адресу
• Грамотный монтаж ТВ приставки
• отсутствие скрытых платежей на весь срок обслуживания
[url=internet-sibirskie-seti.ru]сибсети домашний интернет и тв тарифы[/url]
проверить домашний интернет сибирские сети – [url=https://www.internet-sibirskie-seti.ru /]http://www.internet-sibirskie-seti.ru[/url]
[url=https://image.google.bj/url?q=https://internet-sibirskie-seti.ru/]https://image.google.co.ao/url?q=https://internet-sibirskie-seti.ru/[/url]
[url=http://bookangel.co.uk/boards/threads/hey-folks.364/page-102#post-9839]Домашний интернет и ТВ от «СибСети» в вашем доме[/url] 5c29ee4
Натяжные потолки в Архангельске — быстро,качественно,с гарантией.
Осуществляем проффессиональный монтаж в ванную, на кухню, в комнату, в коридор;
Подберем стильный дизайн натяжных потолков с учётом особенностей помещения;
Выполняем работы любой сложности, предлагаем большой выбор глянцевых полотен.
Рассчитаем стоимость — напишите!
Потолки под ключ в комнате — любая фактура. в Архангельском регионе — с консультацией специалиста-
[url=https://29-potolok.ru/]установка натяжных потолков в архангельске[/url]
монтаж натяжных потолков в архангельске высота – [url=http://www.29-potolok.ru/]https://www.29-potolok.ru[/url]
[url=https://clients1.google.am/url?q=https://29-potolok.ru/]https://image.google.co.bw/url?q=https://29-potolok.ru/[/url]
[url=http://archibo.web-size.de/cropped-01b_3364-jpg#comment-878355]Качественная установка натяжных потолков в Архангельске: быстро, качественно, с гарантией[/url] 00e7465
«СибСети» в Новосибирске предоставляют:
• пакет из 150+ ТВ каналов;
• Точную оценку скорости соединения в вашем доме
• Подбор оптимального сочетания интернета и ТВ под ваши задачи
• Проверку инфраструктуры по вашему адресу
• Профессиональную установку оборудования
• Фиксированные тарифы на весь срок обслуживания
[url=internet-sibirskie-seti.ru]домашний интернет сибсети[/url]
тарифы сибирские сетиа на интернет и телевидение – [url=http://internet-sibirskie-seti.ru]https://www.internet-sibirskie-seti.ru[/url]
[url=https://clients1.google.at/url?sa=t&url=https://internet-sibirskie-seti.ru/]http://www.google.hu/url?q=https://internet-sibirskie-seti.ru/[/url]
[url=https://www.lentech.ie/hello-world/#comment-271257]Интернет и цифровое ТВ от «СибСети» в вашем доме[/url] e484_bc
«Инсис» в Екатеринбурге предоставляют:
• интерактивное ТВ;
• поддержки 24/7;
• Подбор оптимального сочетания интернета и ТВ под ваши задачи;
• Анализ технической доступности по вашему адресу.
[url=https://insis-internet-podkluchit.ru/]тарифы инсис домашний интернет 2026[/url]
тарифы инсис для компьютерного интернета – [url=https://www.insis-internet-podkluchit.ru]http://www.insis-internet-podkluchit.ru /[/url]
[url=http://cse.google.me/url?q=https://insis-internet-podkluchit.ru/]https://images.google.com.bn/url?q=https://insis-internet-podkluchit.ru/[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.guryevsk.forum24.ru/www.prognoz-na-segodnya-na-sport3.ru/www.educ-ua12.ru/www.pereplanirovka-nezhilogo-pomeshcheniya10.ru]Домашний интернет и цифровое ТВ от «Инсис» в Екатеринбурге[/url] 46588f2
«СибСети» в Красноярске предоставляют:
• высокоскоростной интернет до 500 Мбит/с;
• Точную оценку доступных технологий в вашем доме
• Определение оптимального сочетания интернета и ТВ под ваши задачи
• Анализ технической доступности по вашему адресу
• Профессиональную установку роутера
• отсутствие скрытых платежей на весь срок обслуживания
[url=internet-sibirskie-seti.ru/krasnoyarsk]sibirskie seti домашний интернет тарифы[/url]
тарифы сибирские сети для компьютерного интернета – [url=http://internet-sibirskie-seti.ru /]https://internet-sibirskie-seti.ru/krasnoyarsk[/url]
[url=https://maps.google.fr/url?q=https://internet-sibirskie-seti.ru/krasnoyarsk]https://www.google.gl/url?sa=t&url=https://internet-sibirskie-seti.ru/krasnoyarsk[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.chop-ohrana.com/czeny-na-uslugi-ohrany/www.arus-diplom33.ru/www.narkologicheskaya-klinika-25.ru/www.sajt-smart-way.ru/wwwboard.pl,[],[],200,65,0,1126,0,6,9,0,0,https://internet-sibirskie-seti.ru/,%D0%BF%D1%97%D0%85%D0%BF%D1%97%D0%85%D0%BF%D1%97%D0%85y%D0%BF%D1%97%D0%85q%D0%BF%D1%97%D0%85%D0%BF%D1%97%D0%85%D0%BF%D1%97%D0%85u%D0%BF%D1%97%D0%85%D0%BF%D1%97%D0%85%D0%BF%D1%97%D0%85y%5DИнтернет и цифровое ТВ от «СибСети» в Красноярске[/url] 002104a
«Field Fit» предоставляет:
• футболки из быстросохнущей ткани;
• привлекательные цены и скидки до 50-60%;
• Определение оптимального комплекта экипировки под ваш клуб и бюджет;
• Анализ ассортимента в нужной категории.
[url=https://futbolnaya-forma-fieldfit.ru/]футбольная форма недорого москва[/url]
купить футбольную атрибутику – [url=http://futbolnaya-forma-fieldfit.ru]http://www.futbolnaya-forma-fieldfit.ru[/url]
[url=https://toolbarqueries.google.sc/url?q=https://futbolnaya-forma-fieldfit.ru/]https://images.google.co.id/url?sa=t&url=https://futbolnaya-forma-fieldfit.ru/[/url]
[url=http://nick263.la.coocan.jp/TeamCaffeine/wwwboard.cgi/%3C/www.marketing99.ru/www.diploma-dok.ru/r-diploma19.ru]Официальная футбольная форма и футбольные сувениры от «Field Fit» в вашем городе[/url] 545c29e
«Инсис» в Екатеринбурге предоставляют:
• пакет из 150+ ТВ каналов;
• бесплатный монтаж оборудования;
• Определение оптимального тарифа под ваши задачи;
• Проверку возможности подключения по вашему адресу.
[url=https://insis-internet-podkluchit.ru/]insis интернет проверить адрес[/url]
услуги инсиса интернет и телевидение тарифы – [url=http://insis-internet-podkluchit.ru /]http://www.insis-internet-podkluchit.ru /[/url]
[url=https://www.google.com.bn/url?sa=t&url=https://insis-internet-podkluchit.ru/]http://maps.google.tn/url?q=https://insis-internet-podkluchit.ru/[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.pereplanirovka-nezhilogo-pomeshcheniya11.ru/www.melbet5005.ru]Высокоскоростной интернет и ТВ от «Инсис» в Екатеринбурге[/url] e488_a9
«Инсис» в Екатеринбурге предоставляют:
• высокоскоростной интернет до 500 Мбит/с;
• бесплатный монтаж оборудования;
• Подбор оптимального пакета услуг под ваши задачи;
• Проверку технической доступности по вашему адресу.
[url=https://insis-internet-podkluchit.ru/]домашний интернет инсис екатеринбург[/url]
инсис проводной интернет тарифы – [url=http://insis-internet-podkluchit.ru /]https://www.insis-internet-podkluchit.ru[/url]
[url=https://maps.google.bf/url?q=https://insis-internet-podkluchit.ru/]http://cse.google.mv/url?q=https://insis-internet-podkluchit.ru/[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/25kat.ru/music/www.luchshie-prognozy-na-khokkej14.ru/www.1win5521.ru]Высокоскоростной интернет и телевидение от «Инсис» в Екатеринбурге[/url] 002104a
«Зелёная точка» в Ставрополе предоставляют:
• пакет из 150+ ТВ каналов;
• поддержки 24/7;
• Подбор оптимального тарифа под ваши задачи;
• Анализ возможности подключения по вашему адресу.
[url=]зеленая точка домашний интернет проверить адрес[/url]
подключить интернет зеленая точка в квартире ставрополь – [url=http://zelenaya-tochka-podkluchit.ru]https://www.zelenaya-tochka-podkluchit.ru[/url]
[url=https://maps.google.com.ai/url?q=https://zelenaya-tochka-podkluchit.ru]http://ww17.todaygoogle.com/__media__/js/netsoltrademark.php?d=https://zelenaya-tochka-podkluchit.ru[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.guryevsk.forum24.ru/www.arus-diplom6.ru/www.frei-diplom5.ru/melbet5008.ru]Домашний интернет и цифровое ТВ от «Зелёная точка» в вашем доме[/url] 6588f20
«Орион» в Красноярске предоставляют:
• интерактивное ТВ;
• бесплатный монтаж оборудования;
• Подбор оптимального пакета услуг под ваши задачи;
• Анализ инфраструктуры по вашему адресу.
[url=https://orion-inetrnet-podkluchit.ru]орион интернет[/url]
сколько стоит провести интернет в квартиру орион – [url=http://www.orion-inetrnet-podkluchit.ru]http://www.orion-inetrnet-podkluchit.ru[/url]
[url=http://www.google.com.ph/url?q=https://orion-inetrnet-podkluchit.ru]https://www.google.it.ao/url?q=https://orion-inetrnet-podkluchit.ru[/url]
[url=https://zsy6688.com/forum.php?mod=viewthread&tid=1440&pid=420307&page=888&extra=page%3D1#pid420307]Интернет и цифровое ТВ от «Орион» в вашем доме[/url] c29ee48
«СибСети» в Красноярске предоставляют:
• интерактивное ТВ;
• Точную оценку доступных технологий в вашем доме
• Подбор оптимального пакета услуг под ваши задачи
• Анализ технической доступности по вашему адресу
• Профессиональную установку роутера
• Фиксированные тарифы на весь срок обслуживания
[url=internet-sibirskie-seti.ru/krasnoyarsk]сибирские сети домашний интернет проверить адрес[/url]
оптоволокно интернет сибсети – [url=https://www.internet-sibirskie-seti.ru]http://www.internet-sibirskie-seti.ru/krasnoyarsk[/url]
[url=https://clients1.google.bg/url?q=https://internet-sibirskie-seti.ru/krasnoyarsk]https://clients1.google.cat/url?q=https://internet-sibirskie-seti.ru/krasnoyarsk[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.guryevsk.forum24.ru/www.frei-diplom7.ru]Высокоскоростной интернет и цифровое ТВ от «СибСети» в Красноярске[/url] 00e7465
«TUT-SPORT» предлагает:
• гетры, шорты и спортивные костюмы клуба Арсенал;
• доставку по всей России;
• Подбор оптимального набора под ваш клуб и бюджет;
• Проверку ассортимента в нужной категории.
[url=https://tut-sport.ru/tovary/kluby/arsenal]футбольная форма клуба Арсенал купить[/url]
оригинальная футбольная форма клуба Арсенал – [url=https://www.tut-sport.ru/tovary/kluby/arsenal]http://www.tut-sport.ru/tovary/kluby/arsenal[/url]
[url=https://www.google.hn/url?q=https://tut-sport.ru/tovary/kluby/arsenal]http://clients1.google.com.pr/url?sa=i&url=https://tut-sport.ru/tovary/kluby/arsenal[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.pelsh.forum24.ru/www.stretch-ceilings-samara.ru/www.zakazat-onlayn-translyaciyu4.ru]Клубная атрибутика и подарки для фанатов от «TUT-SPORT» в вашем городе[/url] 545c29e
«TUT-SPORT» предлагает:
• футболки из быстросохнущей ткани клуба Айнтрахт;
• доставку по всей России;
• Определение оптимального комплекта экипировки под ваш клуб и бюджет;
• Анализ наличия размеров.
[url=https://tut-sport.ru/tovary/kluby/eintracht]футбольная форма Айнтрахт недорого москва[/url]
футбольная форма Айнтрахт москва – [url=https://www.tut-sport.ru/tovary/kluby/eintracht]https://www.tut-sport.ru/tovary/kluby/eintracht[/url]
[url=https://cse.google.com.bd/url?sa=t&url=https://tut-sport.ru/tovary/kluby/eintracht]https://clients1.google.co.zm/url?q=https://tut-sport.ru/tovary/kluby/eintracht[/url]
[url=http://mongocco.sakura.ne.jp/bbs/index.cgi/idfFxuWnM]Клубная атрибутика и футбольные сувениры от «TUT-SPORT» в вашем городе[/url] 545c29e
«Зелёная точка» в Ставрополе предлагают:
• высокоскоростной интернет до 500 Мбит/с;
• быстрое подключение за 1 день;
• Определение оптимального сочетания интернета и ТВ под ваши задачи;
• Проверку инфраструктуры по вашему адресу.
[url=]сколько стоит подключить интернет зеленая точка[/url]
зеленая точка интернет в квартиру – [url=https://www.zelenaya-tochka-podkluchit.ru]https://www.zelenaya-tochka-podkluchit.ru[/url]
[url=http://alt1.toolbarqueries.google.ro/url?q=https://zelenaya-tochka-podkluchit.ru]http://alt1.toolbarqueries.google.com.tw/url?q=https://zelenaya-tochka-podkluchit.ru[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.ocenka-chasov-onlajn9.ru/www.arenda-mini-ekskavatora-v-moskve-2.ru/url]Домашний интернет и цифровое ТВ от «Зелёная точка» в Ставрополе[/url] e746588
«Орион» в Красноярске предоставляют:
• пакет из 150+ ТВ каналов;
• бесплатный монтаж оборудования;
• Подбор оптимального тарифа под ваши задачи;
• Анализ инфраструктуры по вашему адресу.
[url=https://orion-inetrnet-podkluchit.ru]орион интернет красноярск тарифы для дома[/url]
орион интернет цена и тарифы красноярск – [url=https://www.orion-inetrnet-podkluchit.ru]https://www.orion-inetrnet-podkluchit.ru[/url]
[url=https://cse.google.sr/url?sa=t&url=https://orion-inetrnet-podkluchit.ru]https://cse.google.pn/url?q=https://orion-inetrnet-podkluchit.ru[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/25kat.ru/www.educ-ua18.ru/www.prognozy-na-futbol-10.ru]Интернет и телевидение от «Орион» в вашем доме[/url] 46588f2
«TUT-SPORT» предоставляет:
• гетры, шорты и спортивные костюмы клуба Аталанта;
• привлекательные цены и скидки до 50-60%;
• Подбор оптимального набора под ваш клуб и бюджет;
• Проверку наличия размеров.
[url=https://tut-sport.ru/tovary/kluby/atalanta]клубные футбольные формы Аталанта[/url]
футбольная атрибутика Аталанта в москве – [url=https://www.tut-sport.ru/tovary/kluby/atalanta]http://www.tut-sport.ru/tovary/kluby/atalanta[/url]
[url=https://clients1.google.kz/url?q=https://tut-sport.ru/tovary/kluby/atalanta]http://www.google.ws/url?q=https://tut-sport.ru/tovary/kluby/atalanta[/url]
[url=http://3dim-athin.att.sch.gr/autosch/joomla15/index.php/component/kide/history/-/index.phpoption=com_kide]Клубная атрибутика и подарки для фанатов от «TUT-SPORT» в вашем городе[/url] ee483_c
«Field Fit» предлагает:
• футболки из быстросохнущей ткани;
• привлекательные цены и скидки до 50-60%;
• Подбор оптимального набора под ваш клуб и бюджет;
• Анализ наличия размеров.
[url=https://futbolnaya-forma-fieldfit.ru/]интернет магазин футбольной формы[/url]
футбольная форма купить интернет магазин – [url=https://futbolnaya-forma-fieldfit.ru]http://www.futbolnaya-forma-fieldfit.ru[/url]
[url=https://clients1.google.by/url?sa=t&url=https://futbolnaya-forma-fieldfit.ru/]https://profiles.google.com/url?q=https://futbolnaya-forma-fieldfit.ru/[/url]
[url=https://mafia.mit.edu/viewtopic.php?f=435&t=35982&p=1729571#p1729571]Официальная футбольная форма и подарки для фанатов от «Field Fit» в вашем городе[/url] 002104a
«Зелёная точка» в Ставрополе предоставляют:
• интерактивное ТВ;
• поддержки 24/7;
• Подбор оптимального тарифа под ваши задачи;
• Проверку технической доступности по вашему адресу.
[url=]подключить интернет зеленая точка в квартиру ставрополь[/url]
пакеты зеленая точкаа на интернет и телевидение – [url=http://www.zelenaya-tochka-podkluchit.ru]http://www.zelenaya-tochka-podkluchit.ru[/url]
[url=http://maps.google.pn/url?q=https://zelenaya-tochka-podkluchit.ru]https://images.google.im/url?q=https://zelenaya-tochka-podkluchit.ru[/url]
[url=http://pocherparts.de/cgi-bin/gast4.cgi/t.me/www.rudik-diplom5.ru/market.html]Интернет и цифровое ТВ от «Зелёная точка» в вашем доме[/url] 45c29ee
«СибСети» в Красноярске предлагают:
• интерактивное ТВ;
• Комплексный анализ покрытия сети в вашем доме
• Подбор оптимального сочетания интернета и ТВ под ваши задачи
• Анализ возможности подключения по вашему адресу
• Грамотный монтаж оборудования
• отсутствие скрытых платежей на весь срок обслуживания
[url=internet-sibirskie-seti.ru/krasnoyarsk]подключить домашний интернет в красноярске сибирские сети[/url]
проводной интернет сибсети тарифы – [url=https://internet-sibirskie-seti.ru /]http://internet-sibirskie-seti.ru/krasnoyarsk[/url]
[url=https://maps.google.es/url?sa=t&url=https://internet-sibirskie-seti.ru/krasnoyarsk]https://maps.google.mg/url?q=https://internet-sibirskie-seti.ru/krasnoyarsk[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/25kat.ru/www.educ-ua18.ru/www.pereplanirovka-nezhilogo-pomeshcheniya16.ru/www.r-diploma31.ru]Домашний интернет и телевидение от «СибСети» в вашем доме[/url] a59a545
«Орион» в Красноярске предоставляют:
• интерактивное ТВ;
• быстрое подключение за 1 день;
• Определение оптимального пакета услуг под ваши задачи;
• Проверку возможности подключения по вашему адресу.
[url=https://orion-inetrnet-podkluchit.ru]орион интернет плюс тв[/url]
тарифы ориона на интернет и телевидение – [url=http://www.orion-inetrnet-podkluchit.ru]https://orion-inetrnet-podkluchit.ru[/url]
[url=https://toolbarqueries.google.it/url?sa=i&url=https://orion-inetrnet-podkluchit.ru]https://images.google.com.bd/url?sa=t&url=https://orion-inetrnet-podkluchit.ru[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.pelsh.forum24.ru/www.comedysong.ru/musicset/www.frei-diplom5.ru/www.frei-diplom2.ru/www.gidroizolyaciya-podvala-cena.ru/www.reiting-seo-kompanii.ru/,]Домашний интернет и телевидение от «Орион» в вашем доме[/url] 02104a5
«Field Fit» предлагает:
• широкий выбор форм топ-клубов: ПСЖ, Манчестер Юнайтед, Челси, Реал Мадрид;
• доставку по всей России;
• Определение оптимального набора под ваш клуб и бюджет;
• Проверку ассортимента в нужной категории.
[url=https://futbolnaya-forma-fieldfit.ru/]интернет магазин футбольной формы[/url]
ретро формы футбольных клубов – [url=https://www.futbolnaya-forma-fieldfit.ru]https://www.futbolnaya-forma-fieldfit.ru/[/url]
[url=https://toolbarqueries.google.bi/url?q=https://futbolnaya-forma-fieldfit.ru/]https://images.google.com.tj/url?sa=t&url=https://futbolnaya-forma-fieldfit.ru/[/url]
[url=http://www2.saganet.ne.jp/cgi-bin/hatto/board/wwwboard.pl/www.educ-ua19.ru/s:/%25Evolv.E.L.U.pc@Haedongacademy.org/www.melbetbonusy.ru/www.soglasovanie-pereplanirovki-kvartiry11.ru/www.1xbet-14.com/www.1xbet-10.com/www.frei-diplom2.ru/www.frei-diplom8.ru/www.1xbet-17.com/www.rudik-diplom1.ru/www.zakazat-onlayn-translyaciyu5.ru/www.google.se/www.google.ad/url?q=https://healthyturkiye.com/lechenie-bolezni-pejroni-turcija]Официальная футбольная форма и футбольные сувениры от «Field Fit» в вашем городе[/url] 9ee481_